Эконометрика. №7395(Эконометрика). Задание
 Скачать 66.85 Kb.
|
|
Задание Известны статистические данные по 36 строительным бригадам. Необходимо выяснить влияние различных факторов на величину накладных расходов в строительстве. Известно, что к накладным расходам относятся административно-хозяйственные, коммунальные расходы, дополнительная заработная плата и другие расходы. На качественном уровне выявлено, что фактический уровень накладных расходов оказался наиболее тесно связан со следующими факторами: объемом выполненных работ, численностью рабочих, занятых на строительно-монтажных работах, фондом заработной платы. Остальные факторы были признаны незначимыми. На основании имеющихся данных, необходимо при помощи использования функций Excel: 1. Рассчитать параметры множественной линейной регрессии, проводя процедуру стандартного регрессионного исследования до получения удовлетворительной модели. Провести полный анализ полученного уравнения регрессионной связи. 2. К числу рассчитываемых и анализируемых параметров относятся: а) коэффициенты регрессии (и их значимость); б) коэффициент корреляции (и его значимость); в) коэффициент детерминации; г) стандартные ошибки коэффициентов регрессии; д) доверительные интервалы для коэффициентов регрессии; е) величины общей, объясненной и остаточной дисперсии. 2. На основании реальных и расчетных значений накладных расходов построить графики и сравнить их. Исходные данные
Ход работы а) Находим параметры уравнения множественной регрессии вида 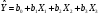 средствами MS Excel. Выбираем «Данные» => «Анализ данных» => «Регрессия». В результате выполнения регрессионного анализа в пакете Excel получены оценкиb0, b1, b2 и b3 и их Р-значения:
Следовательно, уравнение регрессии будет иметь вид: 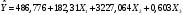 Данное уравнение записано без проверки значимости коэффициентов регрессии. Однако необходимо проверить, все ли из включенных в уравнение параметров действительно оказывают влияние на у. Для коэффициента b0 вероятность его не влияния на у равна 0,8851 (88,51%), что больше порогового значения в 5%, поэтому коэффициент b0 признается не значимым и должен быть удален из модели. Для коэффициента b1 вероятность его не влияния на у близка к нулю, что меньше порогового значения в 5%, поэтому коэффициент b1 признается значимым и оставляется в модели. Для коэффициента b2 вероятность его не влияния на у равна 0,00298 (0,3%), что меньше порогового значения в 5%, поэтому коэффициент признается значимым и должен быть оставлен в модели. Для коэффициента b3 вероятность его не влияния на у равна 0,0075 (0,75%), что меньше порогового значения в 5%, поэтому коэффициент признается значимым и должен быть оставлен в модели. Из модели будет исключена константа. После этого процедура регрессионного анализа проводится заново, для чего в строке «Входной интервал Х» задается те же 3 столбца данных и ставится флажок «Константа – ноль». По полученным результатам вновь оценивается значимость коэффициентов регрессии. На втором этапе полученные результаты могут иметь следующие значения:
Для коэффициента b1 вероятность его не влияния на у близка к нулю, что меньше порогового значения в 5%, поэтому коэффициент b1 признается значимым и оставляется в модели. Для коэффициента b2 вероятность его не влияния на у близка к нулю, что меньше порогового значения в 5%, поэтому коэффициент b2 признается значимым и оставляется в модели. Для коэффициента b3 вероятность его не влияния на у равна 0,0045 (0,45%), что меньше порогового значения в 5%, поэтому коэффициент признается значимым и должен быть оставлен в модели. Окончательное уравнение регрессии запишется в виде: 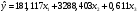 .Регрессионная статистика окончательного уравнения:
б) Коэффициент корреляции равен  , то говорит об очень высокой связи.При выполнении регрессионного анализа в пакете Excel вероятность выполнения нулевой гипотезы для коэффициента корреляции выводится как «Значимость F». Если Значимость F меньше 0,05, то количество наблюдений считается достаточным для признания полученных результатов регрессионного анализа достоверными. Если Значимость F меньше 0,05, то коэффициент корреляции незначим, и количество наблюдений необходимо увеличить. В результате выполнения регрессионного анализа в пакете Excel получено значение R и Значимости F: Множественный R – 0,998571 Значимость F – 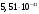 Вероятность незначимости (недостоверности) коэффициента корреляции очень низкая (близка к нулю), значит, исследуется достаточное, количество наблюдений недостаточно. в) При выполнении регрессионного анализа в Excel коэффициент детерминации выводится в таблице «Вывод итогов» как величина R-квадрат. Коэффициент детерминации равен  . Это обозначает, что на 99,71% вариация накладных расходов обусловлена объемом работ, влияние прочих факторов составляет всего 0,29%.г) Стандартная ошибка коэффициента регрессии выводится в регрессионной статистике и равна  . д) доверительные интервалы для коэффициентов регрессии. При выполнении регрессионного анализа в пакете Excel доверительные интервалы автоматически выводятся (наряду с другими результатами) для 95-%-го уровня надежности. В результате выполнения регрессионного анализа в пакете Excel получена оценка b1, b2 и b3и их доверительные интервалы:
Значит:   . е) Таблица дисперсионного анализа имеет вид:
Левая часть (TSS) – общая сумма квадратов отклонений зависимой переменной от ее среднего значения, т.е. общая дисперсия ряда наблюдений. Она характеризует общий разброс зависимой переменной.  Дисперсия y, объясняемая линией регрессии (RSS), измеряется суммой квадратов отклонений между выровненными значениями y и их средним значением.  Дисперсию, которую нельзя объяснить с помощью регрессии, называют оста- точной (ESS). Она характеризует разброс значений зависимой переменной, которые не смогли быть объяснены регрессией, т.е. разброс отклонений фактических значений от выровненных.  Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно. Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований. Оценка факторной дисперсии больше оценки остаточной дисперсии, поэтому можно сразу утверждать не справедливость гипотезы о равенстве математических ожиданий по слоям выборки. Иначе говоря, в данном случае факторный признак оказывает существенное влияния на результативный. Выводы: Регрессионная модель считается качественной, если 1) связь между переменными модели тесная (R0,7), в нашем случае R= 0,99857; 2) в уравнении связи присутствуют лишь значимые факторы (все Р-значения меньше 0,05) в нашем случае Р-значения близко к нулю; 3) наблюдений для достоверных выводов достаточно (Значимость F меньше 0,05), в нашем случае значение F также близко к нулю. На основании того, что эти условия полностью соблюдаются, качество полученной модели является высоким. 2. На основании реальных и расчетных значений накладных расходов построим графики. 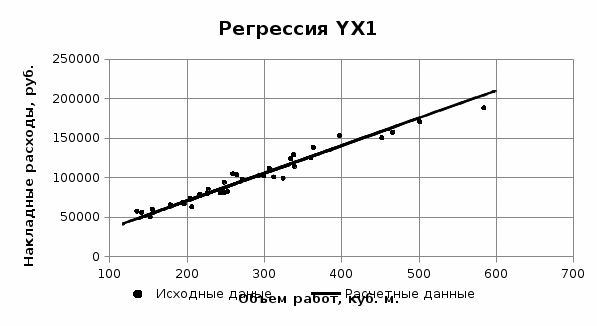   Из графиков видно, что фактические и расчетные значения ненамного отклоняются друг от друга, что говорит о правильности расчетов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||