Задания для лабораторных занятий по Прис у заочников Символьные вычисления
 Скачать 98.7 Kb. Скачать 98.7 Kb.
|
|
Задания для лабораторных занятий по ПрИС у заочников Символьные вычисления Для организации символьных вычислений в общем случае необходимо объявить соответствующие переменные символьными с помощью функции poly следующим образом: var = poly (0, 'var'); здесь var – имя символьной переменной. Другой способ заключается в том, чтобы указать значение символьной переменной в апострофах var = 'выражение' Операции с символьными переменными производят так же, как и с числовыми. Можно строить символьные векторы и матрицы. ЗАДАНИЕ 1Пусть y = x3 + 5x2 - 10, y1 = 2x + 10, z = sinx2 + cos3x. С помощью системы Scilab вычислить: 1. 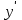 ; 2. ; 2.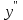 ; 3. ; 3.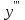 ; 4. ; 4.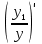 ; 5. ; 5. ; 6. ; 6. Пример выполнения задания 1: пусть в условиях задания y=2x-3, y1=x+1, z=sinx.Тогда для вычисления выражений 1, 2, 4, 6 можно в командном окне Scilab набрать следующие строки: -->x=poly(0, 'x'); d1=derivat(2*x-3), d2=derivat(derivat(2*x-3)), d4=derivat((x+1)/(2*x-3)), j = integrate('sin(x)', 'x', 0, %pi) Завершив ввод нажатием клавиши Enter, получим в командном окне результат вычислений в виде d1 = 2 d2 = 0 d4 = - 5 ----------------- 9 - 12x + 4x2 j = 2. Указание. Для выполнения задания использовать окно редактора системы Scilab. Замечание. Очевидно, функции derivat и integrate служат для вычисления соответственно производных и интегралов в системе Scilab. Для получения справки по синтаксису функций и примерам их использования можно набрать в командном окне команды help derivat и help integrate. Полиномы и полиномиальные матрицы Алгебраическим полиномом степени n называется выражение вида 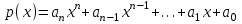 с вещественными коэффициентами с вещественными коэффициентами  Корни полинома – это такие числовые значения неизвестного x, при которых значение полинома p(x) равно нулю. Другими словами, корни полинома – это решения алгебраического уравнения вида Корни полинома – это такие числовые значения неизвестного x, при которых значение полинома p(x) равно нулю. Другими словами, корни полинома – это решения алгебраического уравнения вида 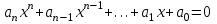 . .Для нахождения корней полинома (то есть для решения соответствующего алгебраического уравнения) удобно использовать функцию roots. Функция roots(p) возвращает вектор-столбец из корней полинома p. Пример. Решить уравнение 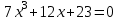 . .-->p= [7 0 12 23];x = roots(p) x = 0.5564046 + 1.6257442i 0.5564046 - 1.6257442i - 1.1128093 Замечание. Коэффициенты полинома следует вводить в порядке убывания степеней переменной x. Если в уравнении отсутствует слагаемое, содержащее, например, x2, то в векторе коэффициентов на соответствующем месте следует набрать 0. Задать алгебраический полином можно по-разному. Способ 1. Использовать команду poly следующего синтаксиса: p = poly(a, 'x', ['flag']) Параметры: a – матрица, вектор или действительное число; x – символьная переменная; 'flag' – строковая переменная, принимающая значение 'roots' или 'coeff'. По умолчанию имеет значение 'roots'. Можно писать сокращенно: 'flag'= 'r' или 'c'. Флаг 'c' означает, что параметр a будет иметь смысл коэффициентов полинома. Флаг 'r' означает, что будет построен полином, корнями которого будут числа, заданные вектором a. Пример. --> poly([-1 0 8], 'x', 'r') ans = - 8x - 7x2 + x3 --> poly([1 2 3], 'x', 'c') ans = 1 + 2x + 3x2 Способ 2. Этот способ является более наглядным. Строка x= poly (0, 'x'); определяет символьную переменную x = 'x'. Теперь можно вводить полином обычным образом. Пример. --> x = poly(0, 'x'); p=3*x^2-7*x+10 p = 10 - 7x + 3x2 Пример. Построить полиномиальную матрицу с элементами p1=1+2x2-3x3 и p2=1-x в первой строке и элементами p1+p2 и p1-p2 во второй строке. --> x = poly(0, 'x'); p1=1+2*x^2-3*x^3; p2=1-x; --> [p1 p2; p1+p2 p1-p2] ans = 1+ 2x2 - 3x3 1 - x 2 - x + 2x2 - 3x3 x + 2x2 - 3x3 Над полиномиальными матрицами можно производить обычные операции. Чтобы получить полиномиальную дробь, можно создать числитель и знаменатель дроби с помощью команды poly и воспользоваться знаком деления. ЗАДАНИЕ 21. Построить полином, корнями которого будут числа 1, 2, 3. Сделать проверку. 2. Найти корни уравнения 5x4 -3x2 +10x - 20=0. 3. Найти произведение полиномов p1 = 3x3 + 2x2 - 10x и p2 = 5x2 - 25x +10 и корни полученного полинома. 4. Найти сумму полиномов p1= 8x4 +12x2 + 3x, p2 = 8x2 - 13x - 70, p3 = 2x4 - 20x +30 и корни полученного полинома. Числовые матрицы ЗАДАНИЕ 3С помощью системы Scilab найти: 1. произведение AB матриц 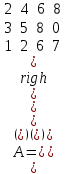 и и  ; ;2. сумму всех элементов матрицы 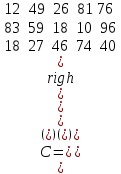 ; ;3. сумму элементов строк и столбцов матрицы C; 4. определитель матрицы 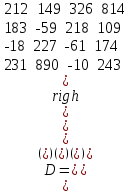 . .Системы линейных алгебраических уравнений ЗАДАНИЕ 4С помощью среды Scilab решить системы линейных алгебраических уравнений: 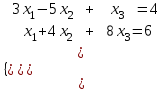 2. 2. 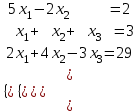 Пример выполнения задания 4: пусть система уравнений имеет вид 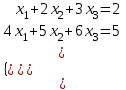 Очевидно, чтобы записать ее в матричном виде, надо учесть, что 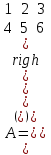 , , 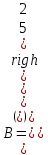 . .Тогда в окне редактора Scilab можно набрать строки: clc // очистка командного окна A=[1 2 3 4 5 6]; B=[2; 5]; x=A\B и, предварительно сохранив файл, подать команду на выполнение. В результате в командном окне получим результат: x = 0.5000 0 0.5000 то есть 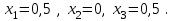 Операторы ввода-вывода Очевидно, простейшим оператором ввода в системе Scilab является оператор присваивания, с помощью которого непосредственно в тексте программы можно ввести значение переменной (скалярной или векторной). Также значение переменной можно ввести непосредственно с клавиатуры или из буфера обмена с помощью функции input: v = input ('Текст'), где v – имя переменной. Оператор input выводит в командное окно строку «Текст» и ждет, пока пользователь введет значение, которое в результате будет присвоено переменной v. Пример. // Вычисление длины окружности r=0; r=input ('Введите радиус окружности r = ); disp('Длина окружности L='); disp(2*%pi*r) Если эту программу набрать в окне редактора, сохранить в виде .sci-файла yyy.sci и запустить, то получим в командном окне: -->Введите радиус окружности r = -->10 Длина окружности L= 62.8318532 Для вывода значения переменной v в простейшем случае достаточно указать имя этой переменной в строке командного окна. В окне редактора для вывода значения переменной v можно использовать функцию disp. Оператор disp(v) выводит на экран значение переменной v без указания имени переменной. Синтаксис команды в общем случае: disp (v1 [, v2, ..., vn]), где v1, v2, …, vn – имена переменных и/или текстовые (символьные) константы. Файлы-сценарии (скрипт-файлы) ЗАДАНИЕ 51. Вычислить значения функции 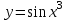 на отрезке [1, 11] с шагом h=2. Вывести на экран все значения аргумента и функции в виде двух столбцов. на отрезке [1, 11] с шагом h=2. Вывести на экран все значения аргумента и функции в виде двух столбцов.2. Вычислить сумму всех значений функции 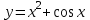 на отрезке [2, 8] с шагом h=0,5. Значение суммы вывести на экран. на отрезке [2, 8] с шагом h=0,5. Значение суммы вывести на экран.3. Для функции  на отрезке [1, 5] вычислить сумму всех отрицательных значений, считая шаг h=0,4. Значение суммы и количество слагаемых вывести на экран. на отрезке [1, 5] вычислить сумму всех отрицательных значений, считая шаг h=0,4. Значение суммы и количество слагаемых вывести на экран.4. Суммировать случайные числа в диапазоне (0, 7) до тех пор, пока значение суммы меньше 17. Дополнительное условие: слагаемые должны лежать в интервале (2; 6). Все слагаемые и промежуточные значения суммы вывести на экран. Пример выполнения задания 5: для функции 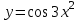 вычислить сумму положительных значений на отрезке [2, 4] с шагом h=0,5. вычислить сумму положительных значений на отрезке [2, 4] с шагом h=0,5. Для решения этой задачи целесообразно набирать соответствующие команды (операторы) в окне редактора. Откроем окно редактора и наберем в нем следующие строки: // Циклические вычисления с условием clc s=0; // начальное значение суммы forx=2:0.5:4; y=cos(3*x^2); if y>0 s=s+y; end end disp(s, 'Значениесуммы') После сохранения набранного .sce-файла и запуска его на решение, получим в командном окне результат s = 2.4213 Если требуется дополнительно вычислить еще и все значения функции y, то в программу надо добавить одну строку: . . . . . . . . . . . . . . . for x=2:0.5:4; y=cos(3*x^2); disp([x, y]) // вывод значений x, y if y>0 s=s+y; end . . . . . . . . . . . . . . . ЗАДАНИЕ 61. Пусть x = 0.397; вычислить значение функции 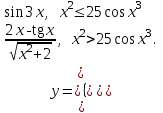 2. Вычислить количество отрицательных элементов заданного вектора произвольной длины. 3. Вычислить количество отрицательных элементов вектора, состоящего из 10 произвольных целых чисел, вводимых с клавиатуры. 4. Вводить с клавиатуры целые числа и суммировать четные, пока сумма ≤10. На экран вывести сумму и количество слагаемых. Файл-функции В случае нескольких выходных параметров файл-функция имеет следующую структуру: function [var1, var2, ...] = f_name (Список входных параметров) // Комментарий Тело файла с любыми выражениями var1= выражение var2= выражение . . . . . . . . endfunction При вызове функции в виде f_name (Список входных параметров) будет возвращаться только значение первого выходного параметра var1. Чтобы получить значения всех выходных параметров, следует использовать обращение к функции вида [var1, var2, . . .] = f_name (Список входных параметров) Пример. Составить программу вычисления значения функции y = sin3(5x) для любого значения х (например, для x = 3). Программу оформить в виде файла-сценария и в виде файла-функции. Сначала запишем файл-сценарий. // Вычисление значения функции (script-file) clc x = input('Введите x='); // x = 3; y = sin(5*x)^3; disp(y, 'y = ') Дальнейшие действия очевидны. Теперь запишем файл-функцию. // Вычисление значения функции (file-function) clc function y = sin_value(x) y = sin(5*x)^3; disp (y, 'y = ', x, 'x = ') endfunction y = sin_value(5) // можно набирать в командном окне ЗАДАНИЕ 71. Составить программу вычисления суммы и произведения n натуральных чисел. Программу оформить в виде файла-функции с одним входным и двумя выходными параметрами. 2. Составить программу, которая вычисляет значения функции y=cosx в n точках, начиная с x=a, с шагом h и суммирует значения y>b. Вывести в командное окно количество слагаемых и значение суммы. Программу оформить в виде файла-функции. Построение графиков функций Для построения графика функции y(x) в простейшем случае используют функцию plot(x, y) или plot2d(x, y). Пример. Построить график функции y=sin(x), если x принимает значения от 0 до 10 с шагом 0,1. --> x = 0:0.1:10; plot(x, sin(x)) Для построения графиков нескольких функций y1(x), y2(x), … , yn(x) в одном графическом окне можно воспользоваться функцией plot(x, y1, x, y2, …, x, yn). Очистить графическое окно можно оператором clf(). Для построения графиков функций в разных графических окнах используют оператор scf (set current figure). Добавить к графику сетку можно командой xgrid. Для расположения нескольких графиков в одном окне без наложения их друг на друга можно использовать операторы subplot или plotframe. Каждый из этих операторов делит графическое окно на несколько областей, однако оператор subplot имеет более простой синтаксис, чем оператор plotframe. Оператор subplot следует указать раньше оператора построения графика. Синтаксис оператора: subplot(m, n, p), где m – количество окон по вертикали, n – число окон по горизонтали, p – номер текущего окна. Для изображения графика функции (дискретной или непрерывной) в виде ступенчатой линии в Scilab существует функция plot2d2(x, y). Она совпадает по синтаксису с функцией plot2d. Для построения анимированных двумерных и трехмерных графиков используют функции comet и comet3d соответственно. С синтаксисом этих функций и особенностями их использования можно ознакомиться с помощью справочной системы среды Scilab 5. 4.0. ЗАДАНИЕ 8Построить графики следующих функций: 1. 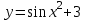 , , 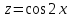 ; ;  , h = 0,25 (в одном графическом окне, пересечение осей задать в точке (0, 0)). , h = 0,25 (в одном графическом окне, пересечение осей задать в точке (0, 0)).2. y = sin(2x+5), 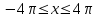 , h = 0,3. График построить ступенчатой линией. Добавить в графическое окно легенду и сетку. Пересечение осей задать в точке (0, 0). , h = 0,3. График построить ступенчатой линией. Добавить в графическое окно легенду и сетку. Пересечение осей задать в точке (0, 0).3. 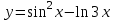 , , 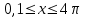 , h = 0,2. Добавить в график общий заголовок и заголовки осей. , h = 0,2. Добавить в график общий заголовок и заголовки осей.4. 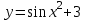 , , 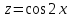 , , 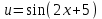 , , 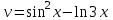 на отрезке на отрезке 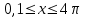 с шагом h = 0,25 в одном графическом окне без наложения. В каждом из четырех подокон привести легенду. с шагом h = 0,25 в одном графическом окне без наложения. В каждом из четырех подокон привести легенду. 5. y = sin(x), z=cos(x) - 0.5, 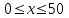 , h = 0,1. Графики функций построить с использованием анимации, в одном графическом окне, разными цветами. , h = 0,1. Графики функций построить с использованием анимации, в одном графическом окне, разными цветами. Решение нелинейных уравнений вида f(x)=0 К нелинейным уравнениям относят алгебраические и трансцендентные уравнения. Алгебраическое уравнение – это уравнение, левая часть которого задана алгебраическим полиномом, то есть имеет вид 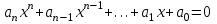 , где , где 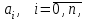 – вещественные коэффициенты. Следовательно, решения (корни) алгебраического уравнения – это корни соответствующего полинома, которые можно искать, например, с помощью функции roots (см. с. 2). Трансцендентным называют уравнение, в котором неизвестная величина является аргументом показательной, логарифмической или тригонометрической функции. – вещественные коэффициенты. Следовательно, решения (корни) алгебраического уравнения – это корни соответствующего полинома, которые можно искать, например, с помощью функции roots (см. с. 2). Трансцендентным называют уравнение, в котором неизвестная величина является аргументом показательной, логарифмической или тригонометрической функции.Численное решение нелинейного уравнения состоит из двух этапов: отделения корня и уточнения корня. При отделении корня ищут отрезок, на котором находится только один корень. На этапе уточнения корень вычисляют с заданной точностью. Для решения нелинейных уравнений в Scilab применяют функцию fsolve(x0, f), где x0 – начальное приближение, f – функция, описывающая левую часть уравнения f(x) = 0. ЗАДАНИЕ 91. С помощью функции fsolve найти на отрезке [-6, 8] корни уравнения 3sinx + 6cos(x+3) – 1 = 0. Левую часть уравнения задать в файле-функции с одним входным и одним выходным параметром. Для отделения корней уравнения предварительно построить график левой части уравнения. 2. С помощью функции fsolve найти все корни уравнения –x2 + 8x + 13cosx – 12 = 0 на отрезке [-3, 5]. Для отделения корней уравнения предварительно построить график левой части уравнения. Численное интегрирование При численном интегрировании вычисляют приближенно  , ,причем подынтегральная функция f(x) может быть задана как аналитически, так и таблицей. При этом функцию f(x), как правило, аппроксимируют функцией Q(x) и вычисляют интеграл от аппроксимирующей функции. При вычислении определенных интегралов численными методами используют функции intsplin, inttrap, integrate, intg. Способ 1. Использование функции intsplin. Это интегрирование экспериментальных данных с помощью сплайн-интерполяции. Значения интегрируемой функции в дискретных точках (узлах) предполагаются заданными. Синтаксис функции: J = intsplin ([x, ] y). Параметры: x – вектор координат x данных; y – вектор координат y данных; J – искомое значение интеграла. Пример. Вычислить интеграл от таблично заданной функции
-->x=1:.4:5; -->y = exp((x-3)^2/8) // значения у в таблице получены // табулированием этой функции -->J = intsplin(x, y) Результат: J = 4.7799684 Способ 2. Использование функции inttrap. Подынтегральная функция между соседними узлами интерполируется линейно. Такой метод называется методом трапеций. Синтаксис функции: J = inttrap ([x,] y). Параметры: x – вектор координат x данных; y – вектор координат y данных (значения интегрируемой функции), yi=f(xi); J – искомое значение интеграла. Вычислим интеграл от той же самой функции --> x = 1:.4:5; y = exp((x-3).^2/8); J = inttrap(x, y) Результат: J = 4.8017553 Способ 3. Использование функции integrate. Это интегрирование по квадратуре. Можно задавать требуемую точность вычислений. Синтаксис функции: J = integrate (expr, v, a, b [, ea [, er]]). Параметры: expr – подынтегральная функция; v – переменная интегрирования; a, b – пределы интегрирования (вещественные числа); ea, er – вещественные числа (предельная абсолютная и предельная относительная погрешности). По умолчанию ea принимает значение 0, er = 1.d-8. Пример: вычислить  . .-->J =integrate('exp((x-3)^2/8)', 'x', 1, 5) Результат: J = 4.7798306 Можно это сделать иначе. Набираем и сохраняем в окне редактора под именем m.sci файл clc function g = m(x) g = exp((x-3).^2/8); endfunction Загружаем этот файл в среду Scilab. Далее в командном окне набираем: -->J = integrate('m', 'x', 1, 5) Результат: J =4.7798306 Способ 4. Использование функции intg. Интегрируемая функция задана либо в виде набора дискретных точек, либо вычисляется с помощью внешней подпрограммы. Можно задавать требуемую точность вычислений. Синтаксис функции: [v, err] = intg (a, b, f [, ea [, er]]) Параметры: a, b – пределы интегрирования (действительные числа); f – внешняя функция (или список строк); ea, er – действительные числа; ea – требуемая абсолютная погрешность точности вычисления (по умолчанию принимает значение 0); er – относительная погрешность точности вычисления (по умолчанию равна 1.d-8); err – оценка абсолютной погрешности результата. Функция f может быть: задана в дискретных узловых точках; именем внешней процедуры, написанной на языке, например Fortran; 3) записана в виде строки как list(f, x1, x2, ...). В итоге для вычисления интеграла набираем -->J = ntg(1, 5, m) // m – описанная выше функция. Результат: J = 4.7798306 З |

 АДАНИЕ 10
АДАНИЕ 10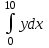 . Вычислить методом трапеций и методом сплайн-интерполяции. Шаг подобрать так, чтобы в результатах совпали первые 4 цифры после десятичной точки.
. Вычислить методом трапеций и методом сплайн-интерполяции. Шаг подобрать так, чтобы в результатах совпали первые 4 цифры после десятичной точки.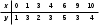 . Для функции вычислить методом трапеций.
. Для функции вычислить методом трапеций.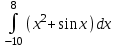 . Вычислить с помощью функции intg, по квадратуре и методом трапеций интеграл
. Вычислить с помощью функции intg, по квадратуре и методом трапеций интеграл