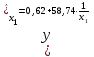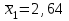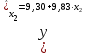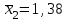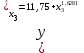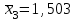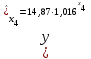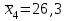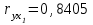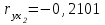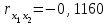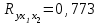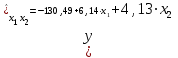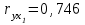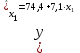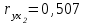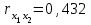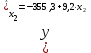задача. Задания для практических занятий к разделу 3 и Раздел Классическая модель линейной регрессии

• Название: Задания для практических занятий к разделу 3 и Раздел Классическая модель линейной регрессии
• Анкор: задача
• Дата: 07.12.2022
• Размер: 45.48 Kb.
• Имя файла: Zadaniya_dlya_prakticheskih_zanyatij_Razdel_3+4.docx
• Тип: Задача; #833708

Задания для практических занятий к разделу 3 и 4.
Раздел 1.3. Классическая модель линейной регрессии

Раздел 1.4. Множественная линейная регрессия
Задача 1. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05 . Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Задача 2. По семи территориям Уральского района за 202Х г. известны значения двух признаков (табл.).

Район	Расходы на покупку продовольственных товаров в общих расходах, %, y	Среднедневная заработная плата одного работающего, руб., x
Удмуртская респ.	68,8	45,1
Свердловская обл.	61,2	59,0
Башкортостан	59,9	57,2
Челябинская обл.	56,7	61,8
Пермская обл.	55,0	58,8
Курганская обл.	54,3	47,2
Оренбургская обл.	49,3	55,2

Требуется:

1. 
   Для характеристики зависимости y от x рассчитать параметры линейной функции.
   
2. 
   Оценить каждую модель через среднюю ошибку аппроксимации и F-критерий Фишера.
   

Задача 3. По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции y от факторов, приведенных в табл.:

Признак-фактор	Уравнение парной регрессии	Среднее значение фактора
Объем производства, млн руб., x1
Трудоемкость единицы продукции, чел.-час, x2
Оптовая цена за 1 т энергоносителя, млн руб., x3
Доля прибыли, изымаемой государством, %, x4

Требуется:

1. 
   Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат.
   
2. 
   Ранжировать факторы по силе влияния.
   

Задача 4. По 30 территориям России имеются данные, представленные табл.

Признак	Среднее значение	Среднее квадратическое отклонение	Линейный коэффициент парной корреляции
Среднедневной душевой доход, руб., y	86,8	11,44	–
Среднедневная заработная плата одного работающего, руб., x1	54,9	5,86
Средний возраст безработного, лет, x2	33,5	0,58

Требуется:

1. 
   Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с ₁ и ₂, пояснить различия между ними.
   
2. 
   Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
   
3. 
   Рассчитать общий и частные F-критерии Фишера.
   

Задача 5. По территориям России изучаются следующие данные (табл. 3.2): зависимость среднегодового душевого дохода y (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых x₁(%) и от доли экономики активного населения в численности всего населения x₂(%).

Признак	Среднее значение	Среднее квадратическое отклонение	Характеристика тесноты связи	Уравнение связи
y	112,76	31,58
x1	5,40	3,34
x2	50,88	1,74

Требуется:

1. 
   Составить таблицу дисперсионного анализа для проверки при уровне значимости =0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи.
   
2. 
   С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактораx₁ после фактора x₂и насколько целесообразно включение x₂послеx₁.
   
3. 
   Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных x₁иx₂ множественного уравнения регрессии.