Задания к самостоятельной работе по механике. Задания к самостоятельной работе по механике Положение равновесия произвольной плоской системы сил
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
Задания к самостоятельной работе по «механике» Положение равновесия произвольной плоской системы сил Задача 1 Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0—С1.9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 20 кН. На раму действуют пара сил с моментом М = 50 кН×м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действует сила F2 под углом 150 к горизонтальной оси, приложенная в точке D, и сила F3 под углом 600 к горизонтальной оси, приложенная в точке Е, и т. д.). Определить реакции связей в точках А,В, вызываемые действующими нагрузками. При окончательных расчетах принять 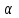 = 0,2 м. = 0,2 м. Указания. Задача 1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении следует учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы 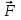 часто удобно разложить ее на составляющие часто удобно разложить ее на составляющие 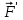 и и 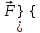 , для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда , для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогдаm0( 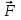 ) = m0( ) = m0(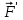 ) + m0( ) + m0(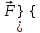 ). ).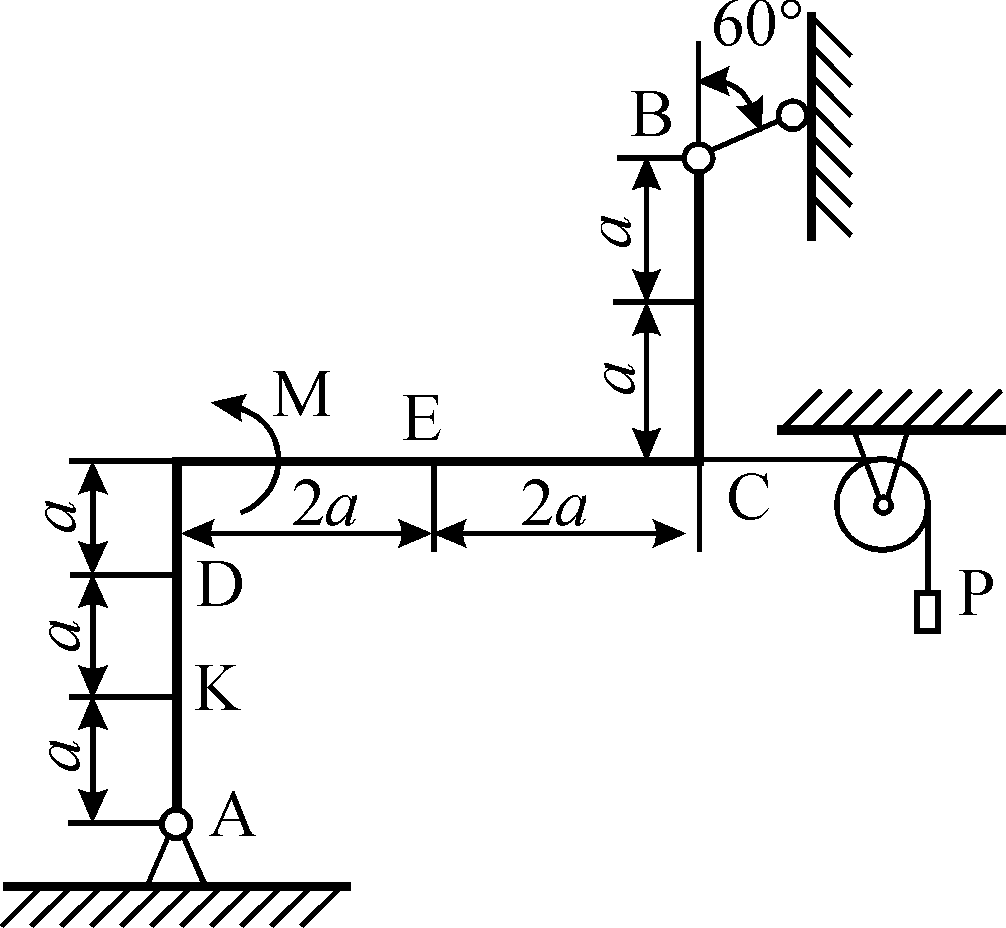 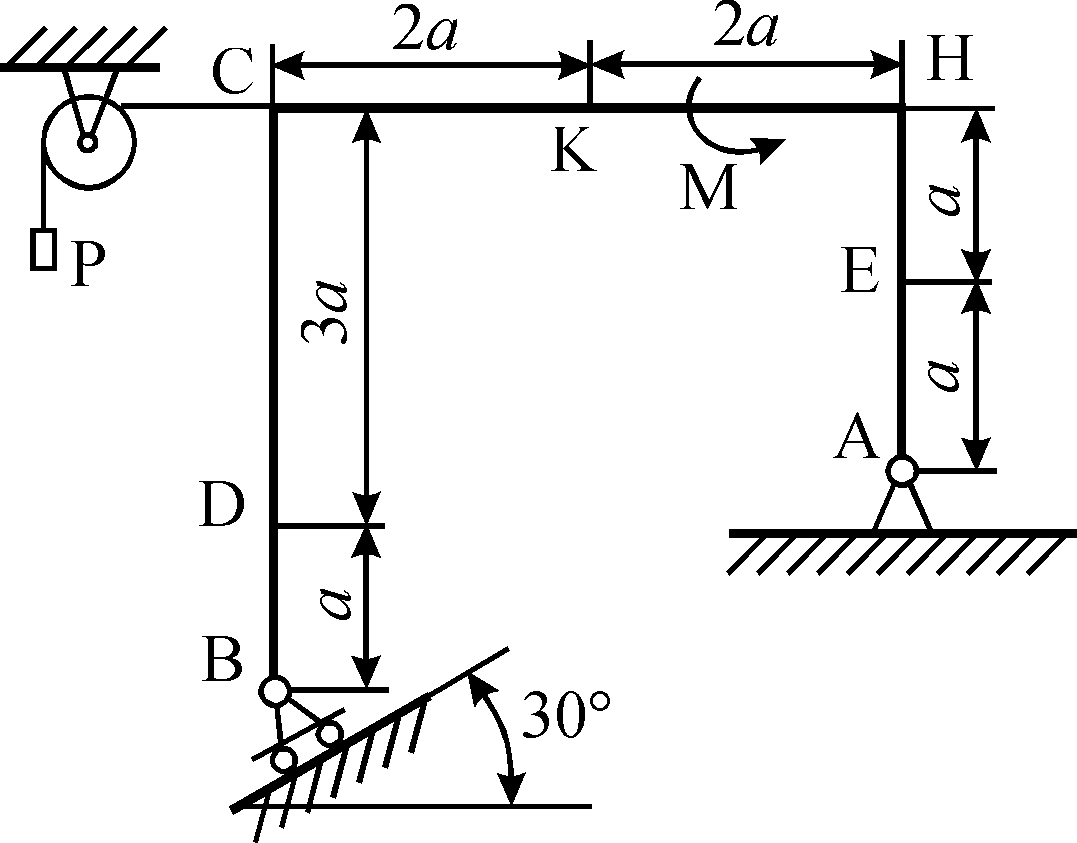 Рис. С1.0 Рис.С1.1  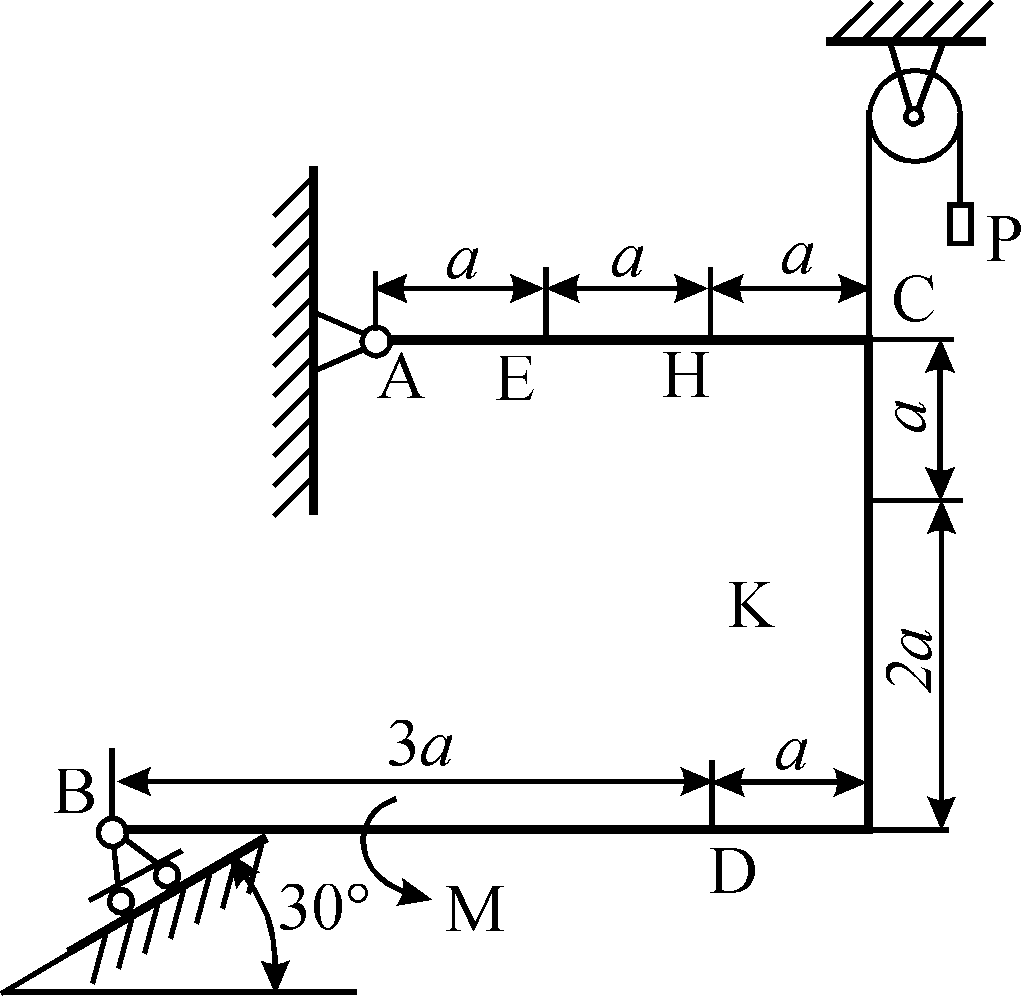 Рис.С1.2 Рис.С1.3 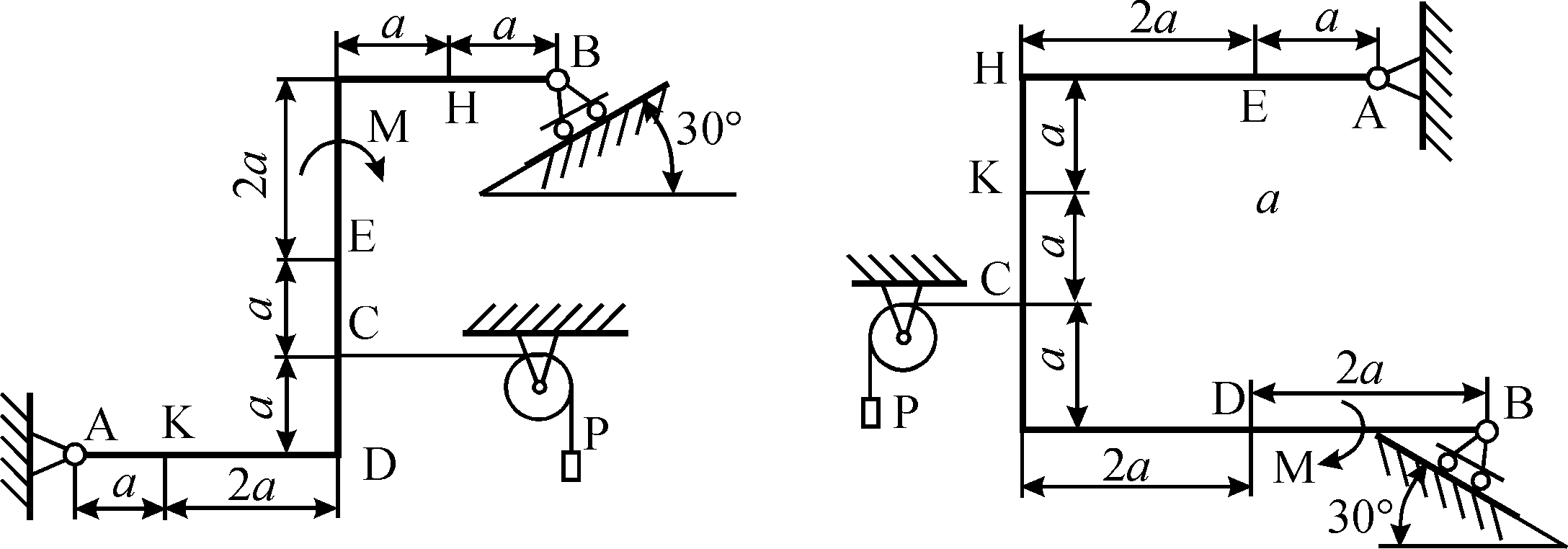 Рис.С1.4 Рис.С1.5  Таблица С1
Задача 2 Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис. С2.0 –С2.5), или свободно опираются один на другой (рис. С2.6 –С2.9). внешними связями, наложенными на конструкцию, являются в точке А или шарнир, или жесткая заделка; в точке В –или гладкая плоскость (рис. С2.0 и С2.1), или невесомый стержень ВВ/ (рис. С2.2 и С2.3), или шарнир (рис. С2.4 – С2.9); в точке D – или невесомый стержень DD/ (рис. С2.0, С2.3, С2.8), или шарнирная опора на катках (рис. С2.7). На каждую конструкцию действуют: пара сил с моментом М =20 кН·м, равномерно распределенная нагрузка интенсивности q =10 кН/м и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С2; там же в графе «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила 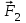 под углом 600 к горизонтальной оси , приложенная в точке L, сила под углом 600 к горизонтальной оси , приложенная в точке L, сила 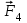 под углом 300 к горизонтальной оси, приложенная в точке Е, и нагрузка, распределенная на участке СК). под углом 300 к горизонтальной оси, приложенная в точке Е, и нагрузка, распределенная на участке СК).Определить реакции связей в точках А, В, С (для рис. С2.0, С2.3, С2.7, С2.8 также и в точке D), вызванные заданными нагрузками. При окончательных расчетах принять а =0,1 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а. Указания. Задача 2 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, следует учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой также неизвестен. 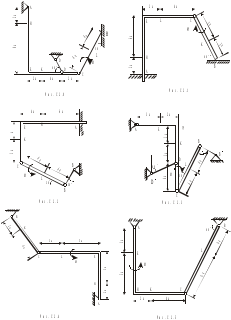 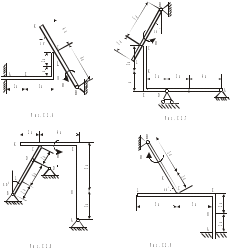 Таблица С2
Таблица С2а
Определение скоростей и ускорений материальной точки по заданным уравнениям движения Задача 3 Под номером 3 помещены две задачи 3а и 3б, которые надо решить. Задача 3а. Точка В движется в плоскости ху (рис. К1.0 –К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х =f1(t), y = f2(t), где х и у выражены в см, t – в секундах. Найти уравнение траектории точки; для момента времени t1= 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Зависимость х = f1(t) указана непосредственно на рисунках, а зависимость y= f2(t) дана в табл. К1 (для рис. К1.0 – К1.2 – в графе 2, для рис. К1.3 – К1.6 – в графе 3, для рис. К1.7 – К1.9 – в графе 4). Задача 3б. Точка движется по дуге окружности радиуса R= =2 м по закону s=f(t), заданному в табл. К1 в графе 5 (s – в метрах, t – в секундах), где s =АМ – расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. определить скорость и ускорение точки в момент времени t1 =1 с. Изобразить на рисунке векторы 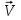 и и 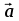 , считая, что точка в этот , считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М. Указания. Задача 3 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t1 =1 с. Таблица К1
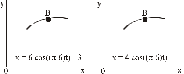 Рис. К1.0 Рис. К1.1 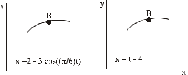 Рис. К1.2 Рис. К1.3 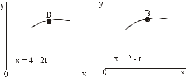 Рис. К1.4 Рис. К1.5 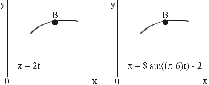 Рис. К1.6 Рис. К1.7 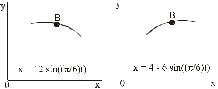 Рис. К1.8 Рис. К1.9 Кинематика поступательного и вращательного движений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


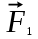
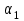
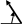
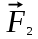
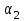

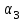
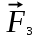

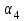
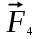





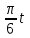 )
)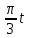 )
)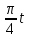 )
)