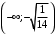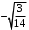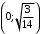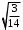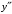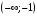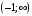Вотввоовво. ЛР№1 Пр. Задания по вариантам. Вариант это номер по журналу. Если номер больше 15, то вычитаем 15. в1

• Название: Задания по вариантам. Вариант это номер по журналу. Если номер больше 15, то вычитаем 15. в1
• Анкор: Вотввоовво
• Дата: 04.10.2021
• Размер: 167.43 Kb.
• Имя файла: ЛР№1 Пр.docx
• Тип: Исследование; #241164

Задания по вариантам. Вариант – это номер по журналу. Если номер больше 15, то вычитаем 15.

в1. Провести исследование функций и построить графики: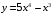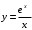


в2. Провести исследование функций и построить графики:





в3. Провести исследование функций и построить графики:


в4. Провести исследование функций и построить графики: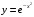



в5. Провести исследование функций и построить графики: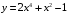


в6. Провести исследование функций и построить графики: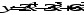


в7. Провести исследование функций и построить графики: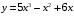


В8. Провести исследование функций и построить графики: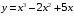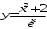


В9. Провести исследование функций и построить графики: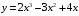


В10. Провести исследование функций и построить графики:


В11. Провести исследование функций и построить графики:


В12. Провести исследование функций и построить графики:


В13. Провести исследование функций и построить графики:


В14. Провести исследование функций и построить графики: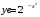


В15. Провести исследование функций и построить графики: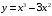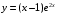


Контрольные вопросы:

1. 
   Что называется производной функции в данной точке?
   
2. 
   Каков физический смысл производной?
   
3. 
   Сформулировать правила дифференцирования.
   
4. 
   Основные табличные производные.
   
5. 
   Монотонности и точки экстремума.
   
6. 
   Выпуклости, вогнутость и точки перегиба.
   

Приложения. Общая схема исследования функции и построения ее графика:

1.Найти область определения функции. Выделить особые точки (точки разрыва) (при построении графика многочлена )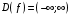

2.Найти точки разрыва, если они есть. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения. Проверить наличие горизонтальных и наклонных асимптот функции. При построении графика многочлена этот пункт пропускаем, асимптот не имеет.

3. Проверить функцию на четность.

4. Найти точки пересечения с осью Оу. Если это возможно, найти точки пересечения с осью Ох и промежутки знакопостоянства

5. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции с помощью первой производной.

6. Найти точки перегиба и интервалы выпуклости-вогнутости с помощью второй производной.

7. Найти дополнительные точки, если в этом есть необходимость.

Построить график функции, используя полученные результаты.
Образец выполнения задания для случая, когда функция не является многочленом:

1. 
   Исследовать функцию и построить график: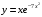
   

Решение:

1. 
   Область определения функции .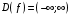
   
2. 
   Функция непрерывна на всей области определения.
   
3. 
   
   

Следовательно, функция является нечетной и ее график симметричен началу координат.

4. 
   Найдем точки пересечения с осями координат: если y=0, то x=0.
   

5. 
   Найдем критические точки: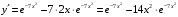
   

x		-
	-	0	+	0	-
		-0,16		0,16

min max

6. 
   Найдем критические точки второй производной: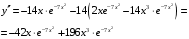
   

=0

x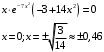
	-	0	+	0	-	0	+
		-0,10		0		0,10

перегиб перегиб перегиб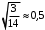

7. 
   Проверяем на наличие асимптот.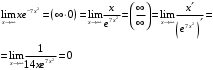
   

Следовательно, - горизонтальная асимптота.

, поэтому наклонной асимптоты нет.

8. 
   Для построения графика находим дополнительные точки: при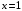
   

2. 
   Исследовать функцию и построить график: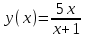
   

Решение.

1.Найдем область определения функции.

.

Выделим точки разрыва: х = -1.

2.Проверим наличие вертикальных асимптот в точках разрыва и на границах области определения:

, следовательно, прямая х= - 1 является вертикальной асимптотой.

Проверим наличие горизонтальных асимптот функции: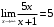

, следовательно, прямая у= 5 является горизонтальной асимптотой.

Проверим наличие горизонтальных асимптот функции: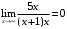

Наклонных асимптот нет.
3.Найдем точки пересечения с осями координат.

Если х=0, то у=0. График проходит через начало координат.

4. Функция не является ни чётной, ни нечётной, т.к. область определения не симметрична 0.

5.Найдем точки экстремума и интервалы монотонности (возрастания и убывания) функции с помощью первой производной:

>0

Следовательно, функция возрастает на промежутках .

6.Найдем точки перегиба и интервалы выпуклости-вогнутости с помощью второй производной: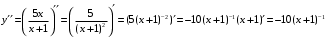

x		-1
	+	не существует	-
		не существует

7. Найдем промежутки знакопостоянства: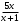

>0 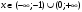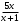при ,

<0 при

8. Найдем дополнительные точки:

х	-2,5	2
у	8,3333	3,3333

9.Построим график функции, используя полученные результаты.