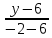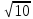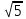соч по математике. СОЧ-4-передел. Задания суммативного оценивания за 4 четверть по предмету Геометрия 1
 Скачать 47.01 Kb. Скачать 47.01 Kb.
|
|
Задания суммативного оценивания за 4 четверть по предмету «Геометрия» 1 вариант Составьте общее уравнение прямой проходящей через точки А(2;6) и В(-4;0) [2] Точки О(0;0), А(5; 5), C(1;3) и B являются вершинами параллелограмма. Найдите абсциссу точки B . 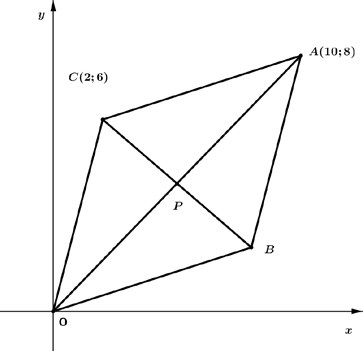 [3] [3] 3. Даны точки А, В, С. Если А(-4; 2) и С(-1; -1) являются серединой отрезка АВ, то найдите координаты точки В. [4] 4. а) Изобразите окружность, соответствующей уравнению (x −5)2 + (y −10)2 =25 . b) Определите взаимное расположение прямой y = 5 и окружности (x −5)2 + (y −10)2 =25 . [4] 5. Докажите, что четырехугольник с вершинами А (1;2), В (4;-1), С(8;3), D(5;6) является прямоугольником. [7] Задания суммативного оценивания за 4 четверть по предмету «Геометрия» вариант 1.Составьте общее уравнение прямой проходящей через точки А(2; 6) и В(-4;-2) [2] Точки О(0;0), А(9; 7), C(2; 5) и B являются вершинами параллелограмма. Найдите абсциссу точки B .  [3] [3] 3. Даны точки А, В, С. Если А( -4; -2) и С(-1; 1) являются серединой отрезка АВ, то найдите координаты точки В. [4] 4. а) Изобразите окружность, соответствующей уравнению (x −2)2 + (y −5)2 =16 b)Определите взаимное расположение прямой y=8 и окружности(x −2)2 + (y −5)2 =16 [4] 5. Докажите, что четырехугольник с вершинами А(-3;-2), B (3;0), С(1;6), D (-5;4) является квадратом. [7]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

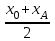 ; Ур=
; Ур=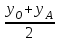
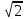
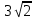
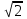
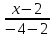 =
=