Захаренков в. Ф. Решения обратной и прямой задач внутренней баллистики Обратная задача внутренней баллистики
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
ЗАХАРЕНКОВ В.Ф. Решения обратной и прямой задач внутренней баллистики 1. Обратная задача внутренней баллистики Решение ОЗВБ ставит своей целью поиск оптимального сочетания конструктивных размеров канала ствола (свободного начального объема Формулировка ОЗВБ, данная выше, является обобщенной и ей отвечает бесчисленное множество решений. Задача проектировщика - быстро найти среди этого множества решений оптимальное. Для поиска оптимального решения требуется проведение большого количества расчетов в итерационном цикле. Задача решается по периодам явления выстрела на основе аналитического метода профессора Н.Ф. Дроздова. Предварительный (пиростатический) период. Этот период начинается с момента воспламенения заряда и заканчивается в момент достижения давления в канале ствола, равного давлению форсирования 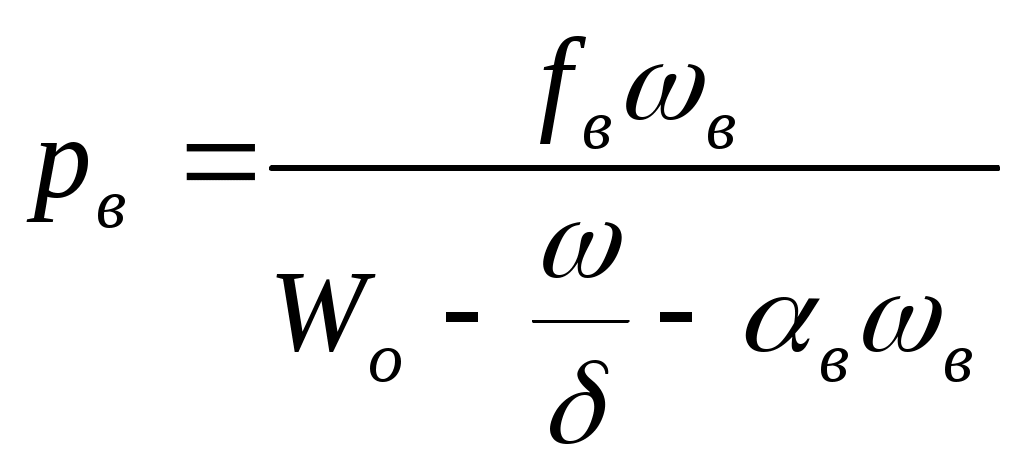 (1) (1)Если давление воспламенителя задано, то из (1) легко найти массу воспламенителя: . 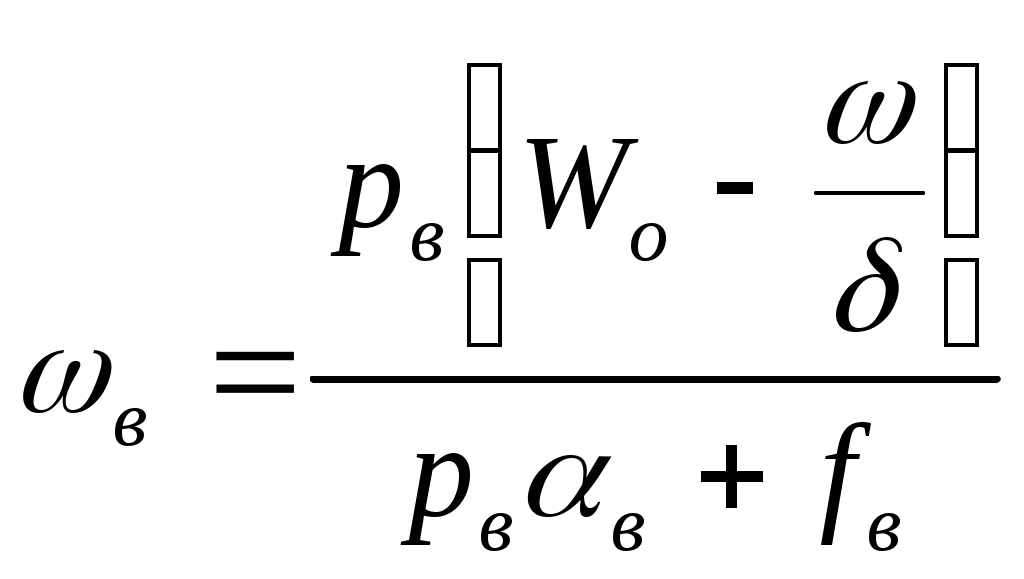 (2) (2)Основное уравнение пиростатики с учетом давления воспламенителя имеет вид 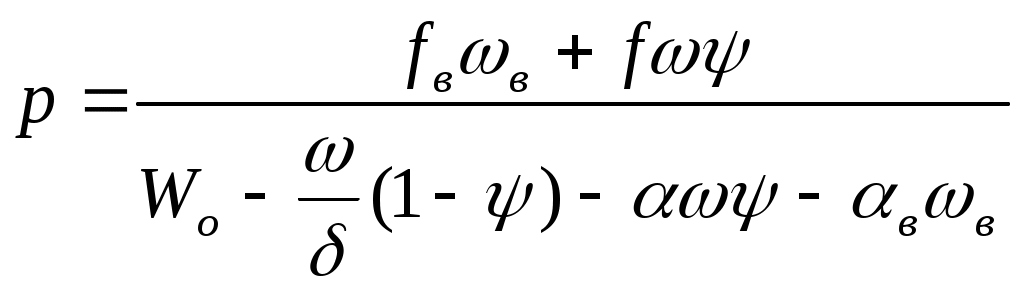 (3) (3)или 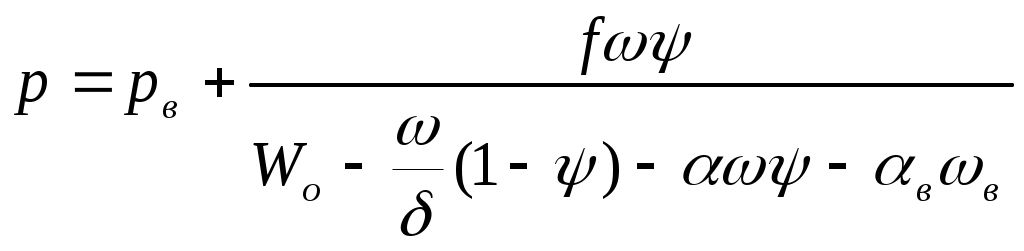 (4) (4)Уравнение (4) позволяет найти долю заряда, сгоревшего в предварительном периоде 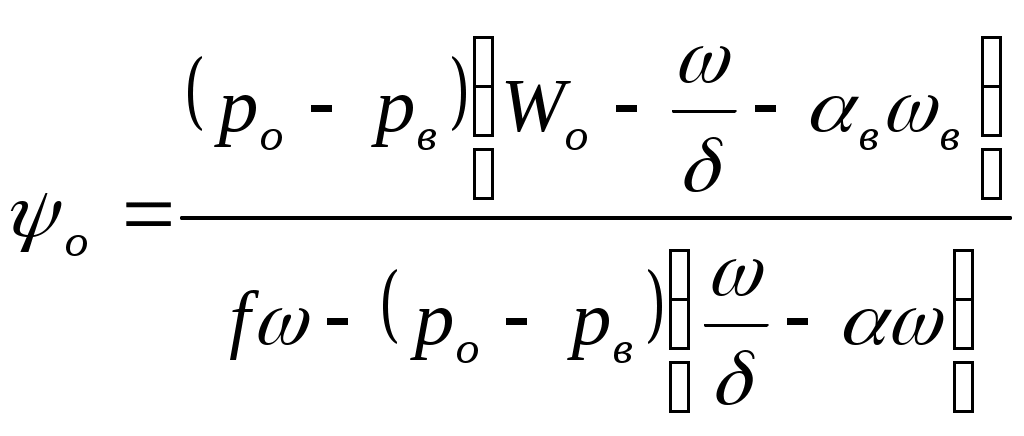 (5) (5)Вводя плотность заряжания . 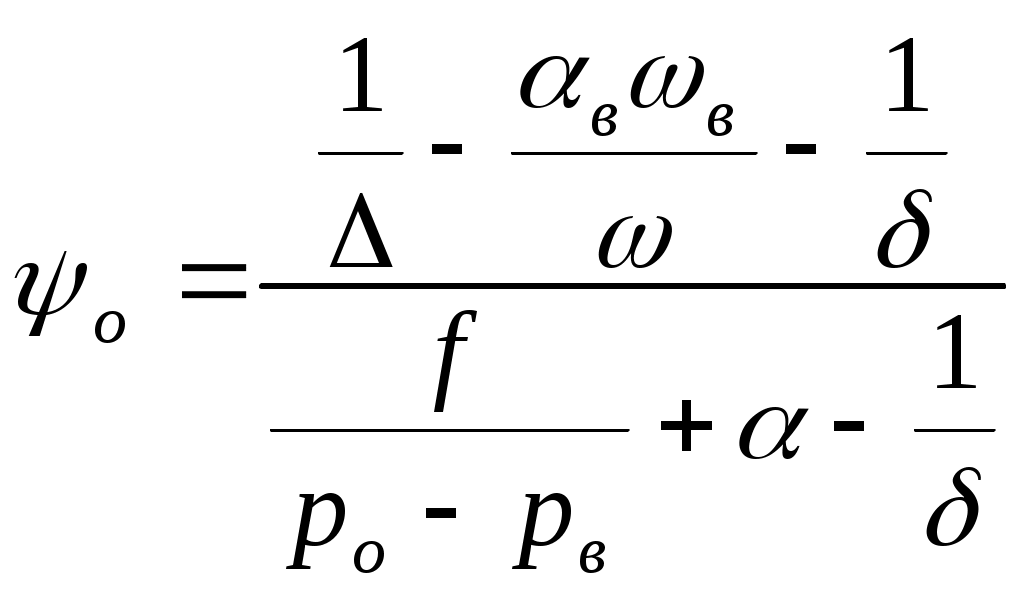 (6) (6)Если пренебречь влиянием массы воспламенителя по сравнению с массой заряда, то уравнение (6) можно записать как . 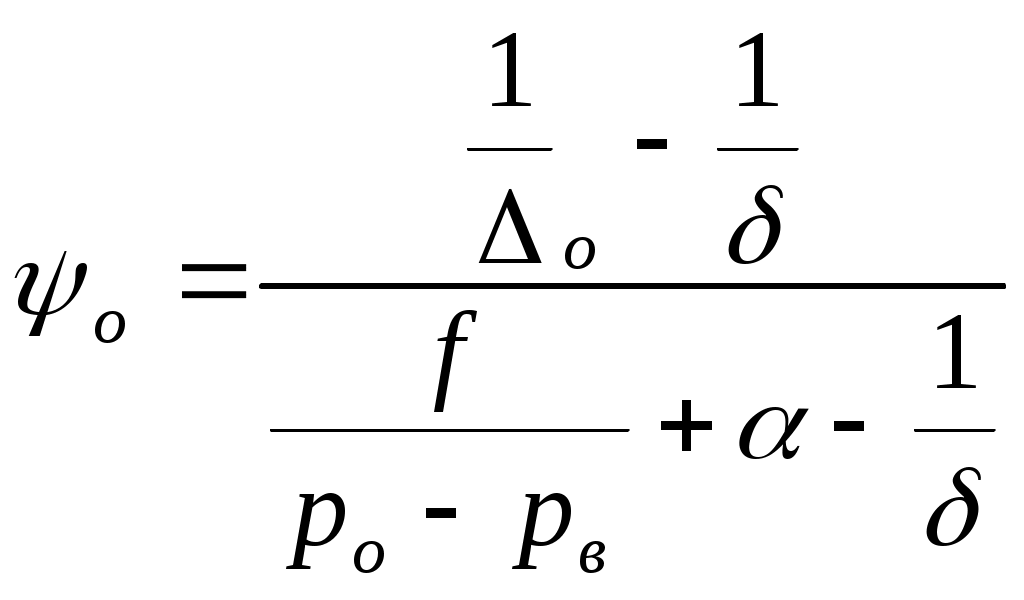 (7) (7)Теперь, зная найти относительную толщину пороха, сгоревшую к началу движения снаряда. Уравнение (8) может быть решено численно, либо методом Кордана, а в случае двухчленного представления аналитически: . 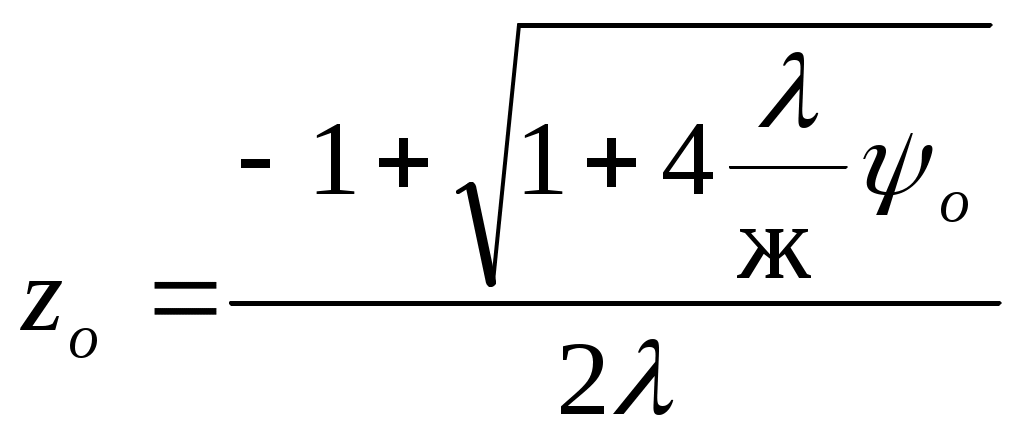 (10) (10)Подкоренное выражение в (10) можно преобразовать, если воспользоваться уравнением поверхности горения порохового зерна, которое в случае двучленного представления имеет вид . Сравнивая (10) и (11), находим . Зная параметры Тогда приведенная длина свободного объема каморы в момент начала движения снаряда . Время предварительного периода может быть рассчитано из основного уравнения пиростатики в дифференциальной форме: . Правая часть (14) из-за сложного характера изменения параметров . Тогда уравнение (14) запишется 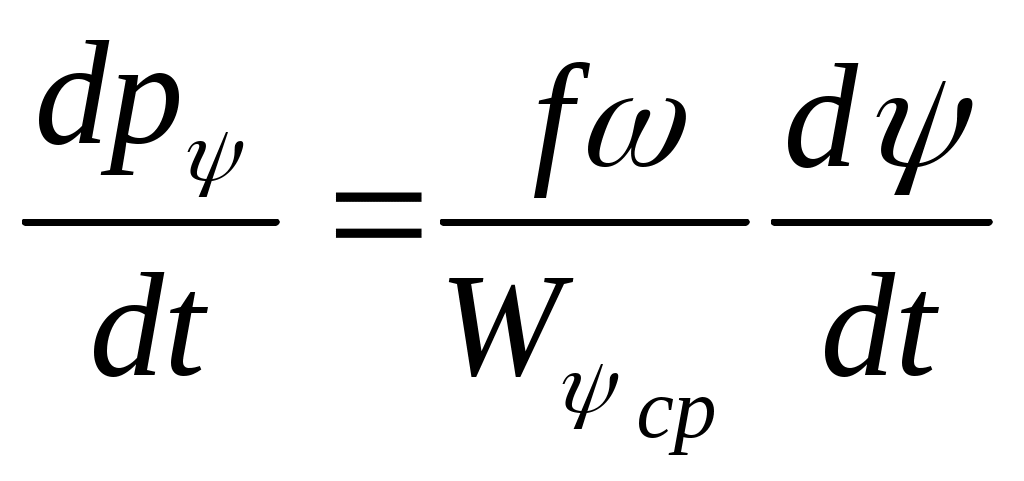 . (16) . (16)Для расчета скорости газообразования Для трубчатого или ленточного пороха поверхность при горении изменяется мало, поэтому в (17) можно положить 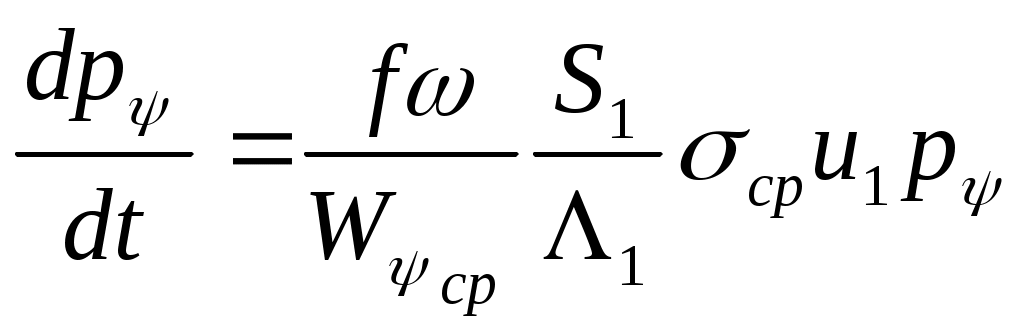 (18) (18)Обозначив , 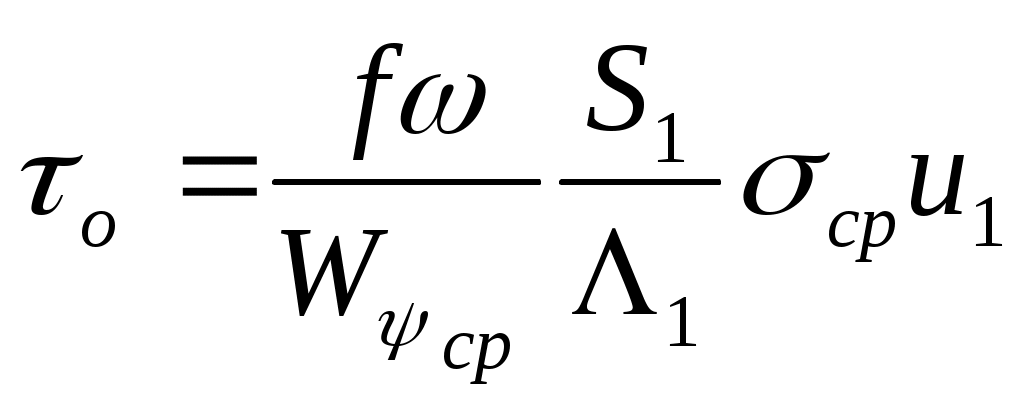 (19) (19)находим . Интегрирование (20) дает 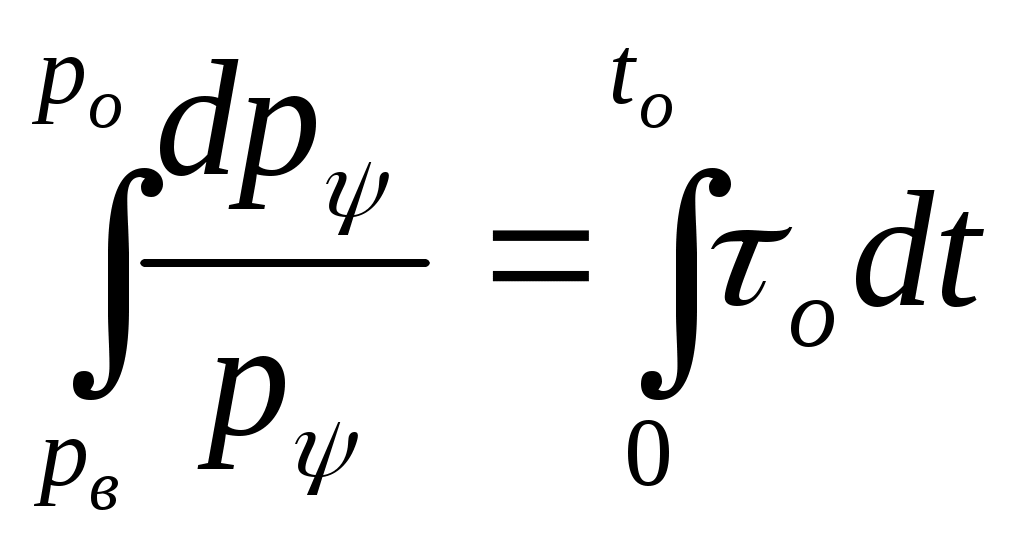 . Отсюда находим . Отсюда находимПоскольку и известные величины, то из (21) находим время предварительного периода . Пиродинамический период. Пиродинамический период - это период, когда относительная степень Для расчета пиродинамического периода воспользуемся упрощенной системой дифференциальных уравнений внутренней баллистики: 1. Закон скорости горения . 2. Уравнение движения снаряда . 3. Закон газообразования . 4. Основное уравнение пиродинамики: . Задача заключается в нахождении зависимостей, связывающих четыре переменные величины: Найдем скорость снаряда v. Для этого преобразуем уравнение движения снаряда (24) следующим образом . 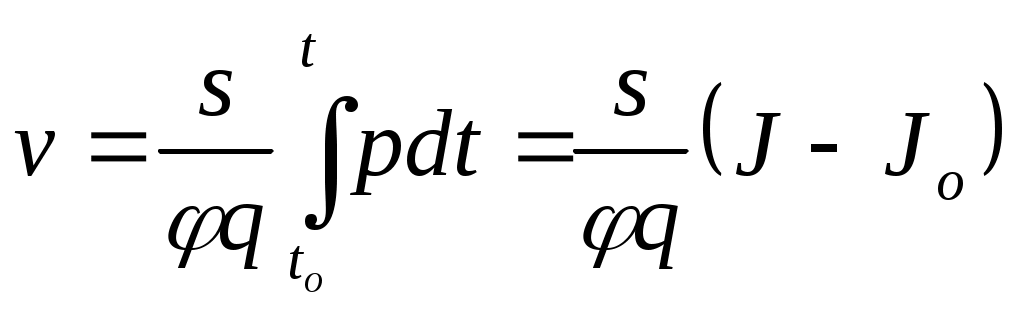 (27) (27)Умножим и разделим правую часть (27) на импульс горения пороха Обозначив Для конца горения пороха (28) принимает вид Найдем путь снаряда Обозначив предельную скорость снаряда при заданных условиях заряжания как находим 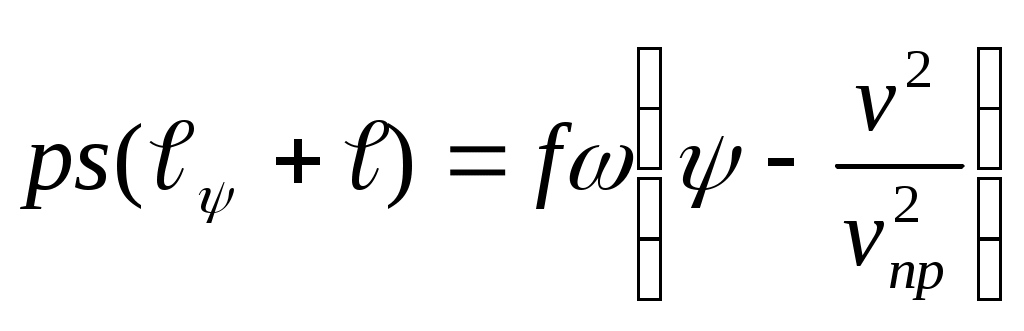 . (32) . (32)С другой стороны, уравнение движения снаряда (24) может быть представлено в виде Решаем (32) и (33) совместно: 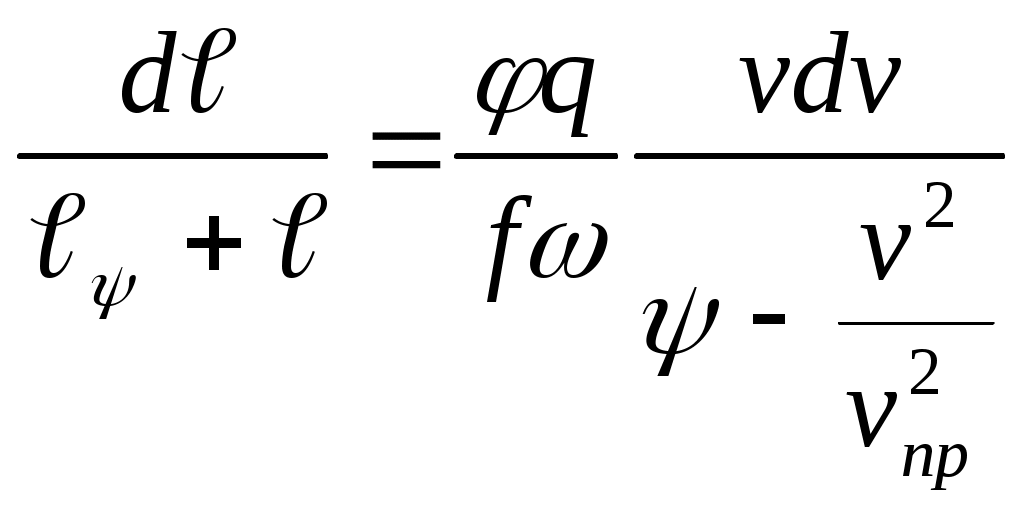 . (34) . (34)Решение уравнения (34) в 1903 г. дал профессор Н.Ф.Дроздов. В качестве независимой переменной он принял величину . Для дальнейших преобразований воспользуемся уравнением (25), подставив в него (35), тогда где Подставляя в (34) уравнения (28) и (36), после алгебраических преобразований находим . Обозначая и и подставляя Величина B называется параметром условий заряжания профессора Дроздова. Интегрирование уравнения (40) возможно, если величина . Так как 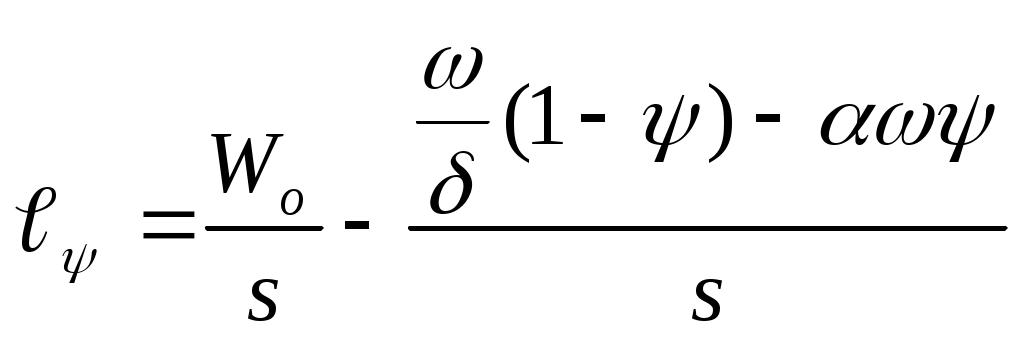 . Величина . Величина называется приведенной длиной каморы. С учетом 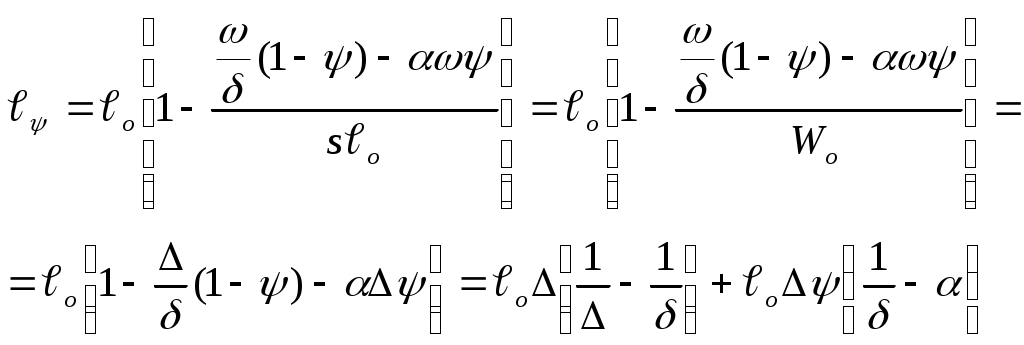 Обозначив далее найдем По аналогии с (43) После этого запишем (40) в виде Решение уравнения (45) имеет вид Где . Расчет среднебаллистического давления в рассматриваемом периоде ведется по основной зависимости пиродинамики (32). Из (32) находим 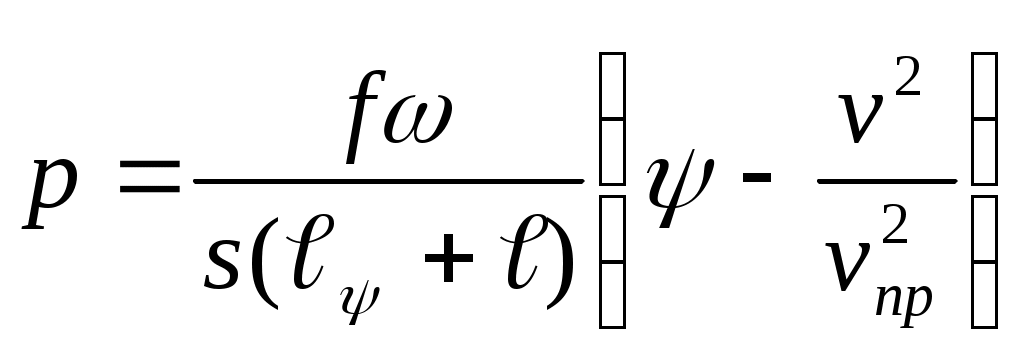 , которое c учетом формул (28), (31) и (38) легко преобразуется к виду , которое c учетом формул (28), (31) и (38) легко преобразуется к видуТермодинамический период. Термодинамический период протекает с момента сгорания порохового заряда до момента прохождения снарядом дульного среза ствола. В этом периоде снаряд продолжает движение под действием расширяющихся пороховых газов. В качестве независимой переменной в этом периоде берется величина пути снаряда, которая изменяется от Для получения расчетных формул воспользуемся уравнением адиабаты где Из (52) где объемы Подставляя эти объемы в (53), находим 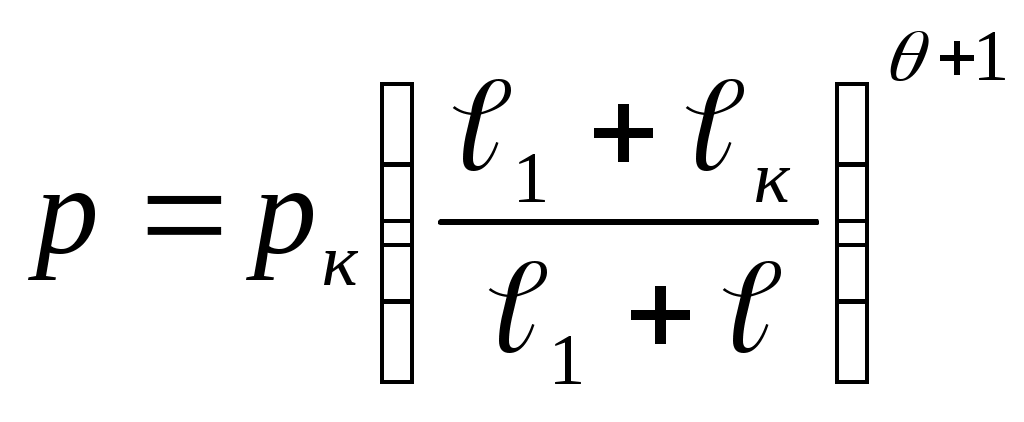 . (54) . (54)Для расчета скорости снаряда в пиродинамическом периоде воспользуемся основным уравнением пиродинамики (26), записав его для условия, когда весь пороховой заряд сгорел ( Обозначая или (55) можно переписать в виде 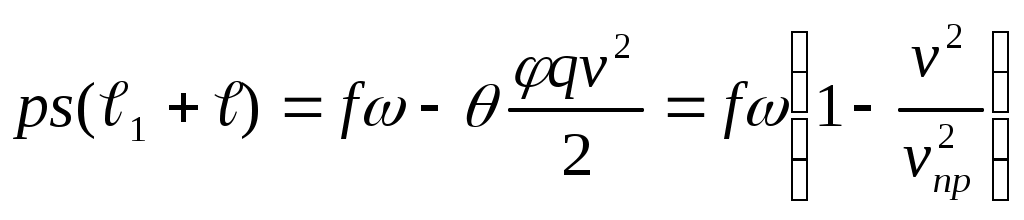 . (58) . (58)При 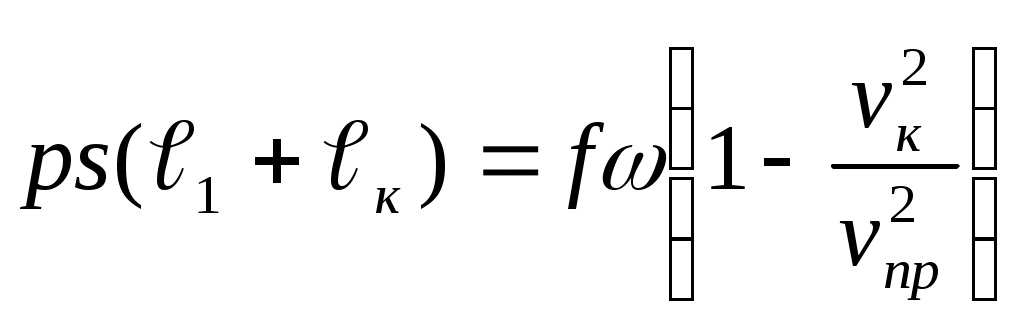 . (59) . (59)Разделив (58) на (59), найдем 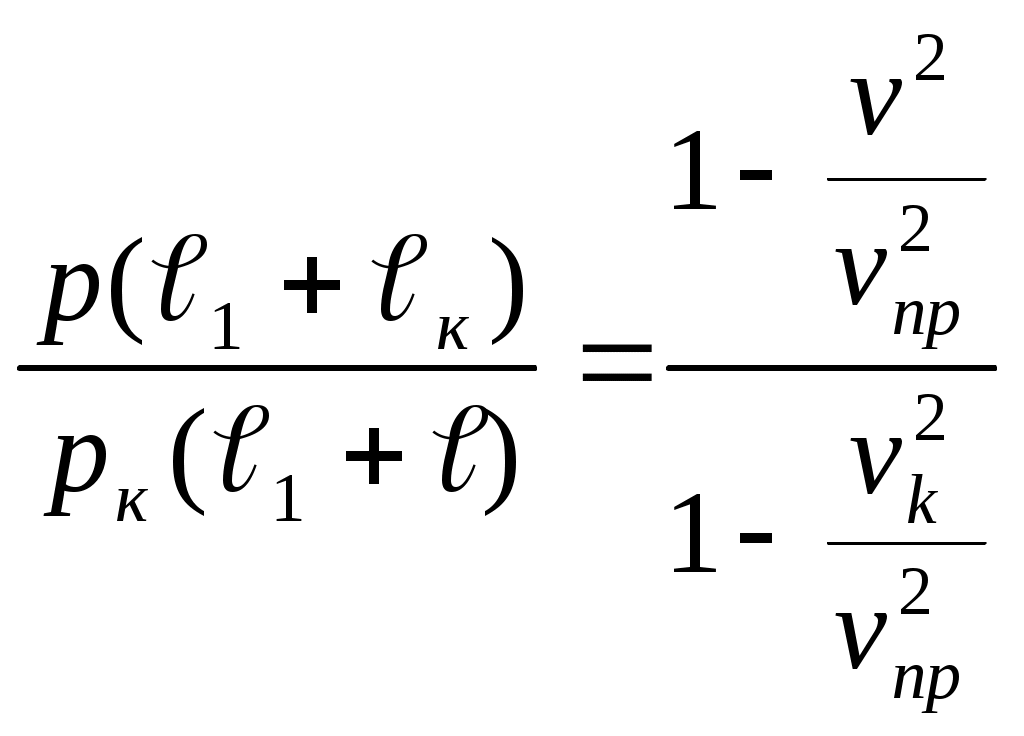 . (60) . (60)Подставив в (60) уравнение (54), находим 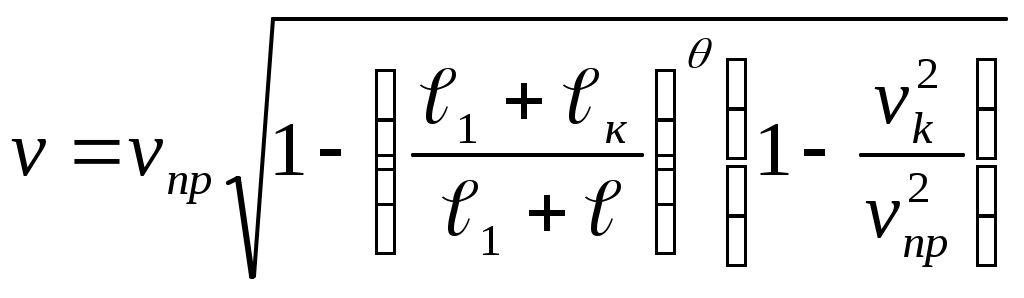 (61) (61)В уравнениях (54) и (61) 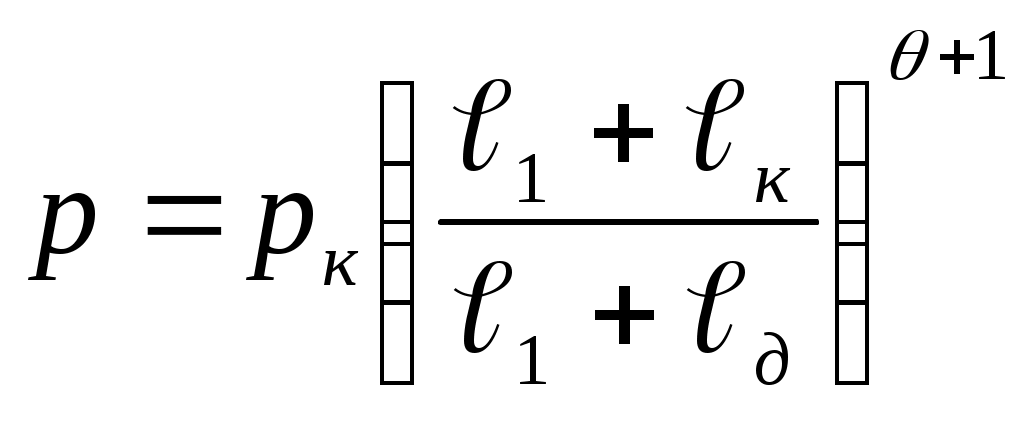 ; (62) ; (62)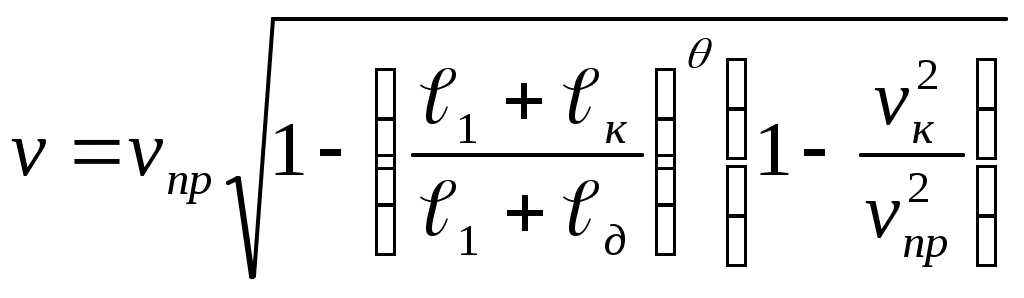 . (63) . (63)Алгоритм решения обратной задачи внутренней баллистики (ОЗВБ) 1. Исходные данные для проектирования: калибр d; масса снаряда q; дульная скорость снаряда коэффициент В.Е.Слухоцкого коэффициент учета глубины нарезов давление форсирования сила пороха f; плотность пороха коволюм характеристики формы порохового зерна показатель процесса 2. Для ускорения поиска оптимального решения в практике решения артиллерийских задач широкое распространение нашел подход, базирующийся на опыте проектировании АО и опирающийся на экспериментальную статистику. Этот опыт обобщен в виде таблиц-эвристик, связывающих дульную энергию АО Таблица 1  3. По 4. По значению 5. Масса порохового заряда 6.Коэффициент фиктивности массы снаряда 7. Максимальное среднебаллистическое давление 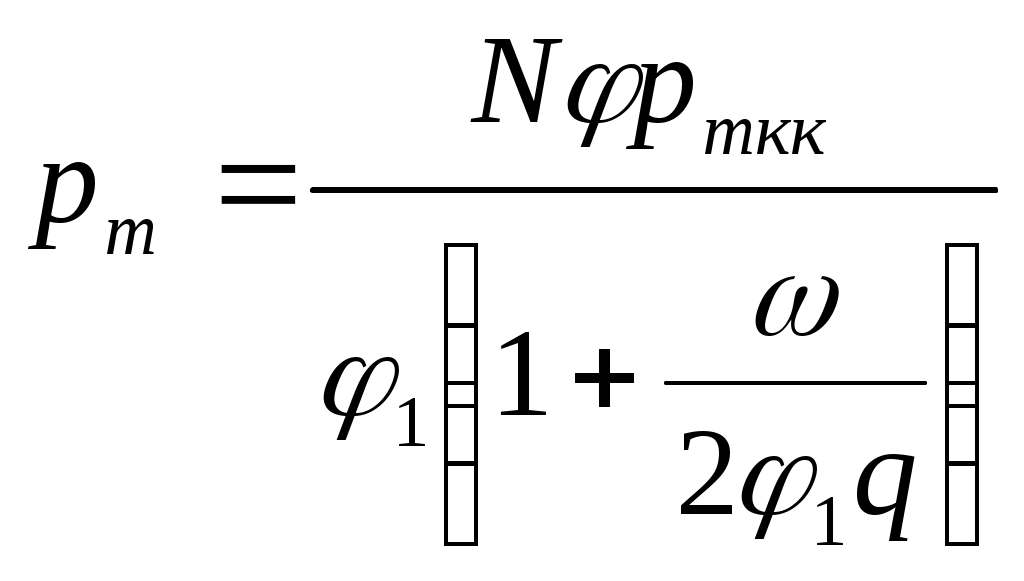 . .8. Начальный свободный объем каморы 9. Площадь канала 10. Приведенная длина каморы 11. Относительная весовая доля порохового заряда, сгоревшего к моменту достижения давления форсирования 12. Относительная поверхность порохового зерна к моменту достижения давления форсирования 13. Относительная толщина в момент достижения давления, равного давлению форсирования 14. Относительная толщина 15. Коэффициент 16. Для проведения дальнейших расчетов необходимо знать параметр заряжания Дроздова 17. Вычисляем 18. 19. 20. 21. Задаемся числом точек разбиения 22. x=0. 23. 24. 25. 26. 27. 28. 29. 30. 31. Путь снаряда 32. Среднебаллистическое давление 33. Подбор давления ведется до достижения условия 34. При выполнении условия точности поиска решения фиксируются 35. Для конца горения 36. Импульс горения 37. Скорость снаряда в конце сгорания заряда 38. Число объемов расширения газа 39. Предельная скорость снаряда 40. Приведенная длина 41. Длина пути снаряда по каналу ствола 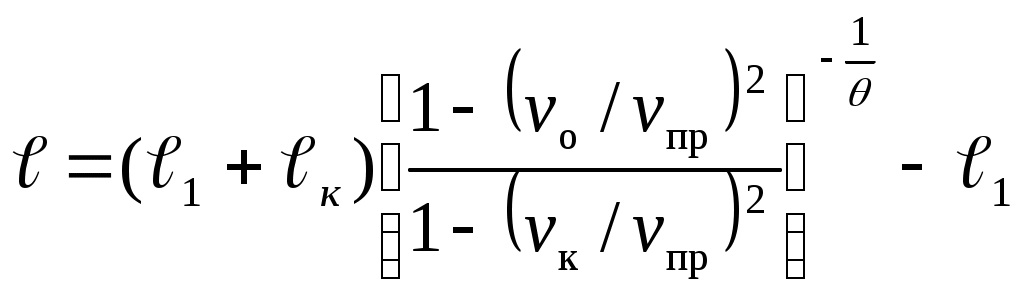 42. Число объемов расширения канала ствола на пути 43. Дульное давление 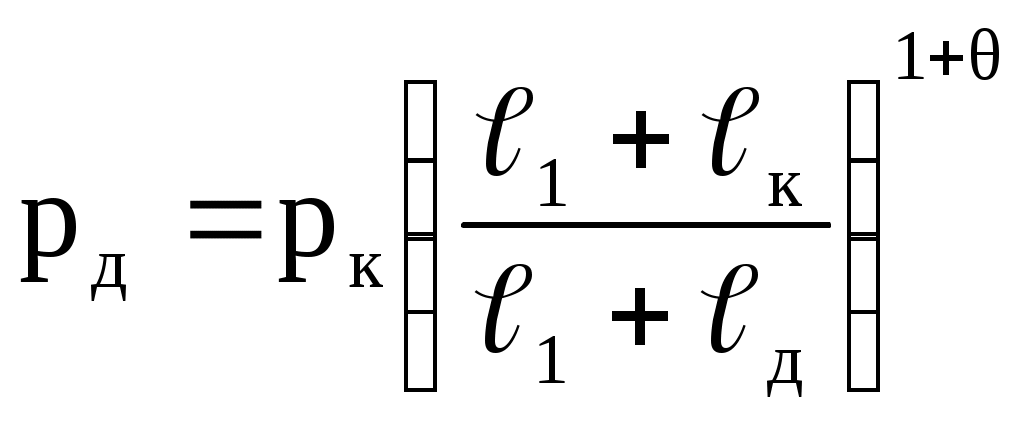 . .44. Длина каморы 45. Длина канала ствола 46. Длина канала в калибрах 47. Объем канала ствола 48. Относительная координата конца сгорания порохового заряда 49. Толщина свода горения порохового зерна 50. Среднее давление газов за время выстрела 51. Коэффициент заполнения индикаторной диаграммы (см. рис.1). Он представляет собой отношение площади кривой давления по пути снаряда к площади прямоугольника, ограниченного величиной максимального давления и длиной пути снаряда по каналу ствола. Коэффициент показывает, какую часть работы совершает газ на метание снаряда от работы, которую бы эти газы могли совершить при сохранении величины максимального давления на всем пути движения снаряда. Величина лежит в пределах от 0,40 до 0,65. 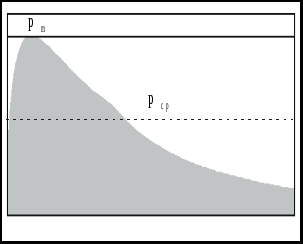 Рис.1 52. Условная баллистическая живучесть ствола 53. Информационный поток на выходе: коэффициент могущества орудия коэффициент использования массы снаряда коэффициент использования массы заряда коэффициент заполнения индикаторной диаграммы условная живучесть ствола начальный объем каморы приведенная длина каморы масса порохового заряда действительная длина каморы степень уширения каморы путь снаряда по каналу ствола длина канала ствола длина канала в калибрах число дульных объемов расширения газа действительная координата конца горения пороха относительная координата конца горения пороха площадь поперечного сечения канала ствола объем канала ствола плотность заряжания коэффициент фиктивности массы снаряда максимальное крешерное давление максимальное среднебаллистическое давление среднебаллистическое давление в конце сгорания порохового заряда среднее давление пороховых газов скорость снаряда в момент сгорания порохового заряда импульс горения пороха толщина свода горения порохового зерна 54. Полученный вариант решения анализируется на возможность удовлетворения технического задания (ТЗ). Если решение не удовлетворяет ТЗ производится корректировка требуемой величины максимального давления Рекомендации по выбору параметров: Таблица 2  Опорный вариант, полученный с использованием эвристической таблицы, отражается (высвечивается) на экране дисплея) в первой колонке табл.3. Таблица 3  Для выбора оптимального варианта необходимо проанализировать данные столбцов таблицы, заполнение которых производится последовательно по мере счета. Параметры в столбцах, для которых расчеты не проводились, обнулены. Если из представленных вариантов решений ни один проектировщика не удовлетворяет, необходимо выбрать наилучший (например вариант 5 в табл.3). В этом случае выбранный вариант перемещается в первую колонку, а остальные варианты обнуляются (табл.4). После этого поиск может быть продолжен. Таблица 4.  Для поиска оптимального (или рационального) варианта решения необходимо исходить из назначения орудия, способа его транспортировки, уровня автоматизации и т.д., а также удовлетворения выходных параметров заданным ограничениям. Рекомендации по условиям выбора основных параметров баллистики приведены в табл.5. Таблица 5.  Количественное значение величины сверху ограничено прочностью снаряда и ствола, а снизу - обеспечением условия взведения взрывателя, стабильности горения пороха, обтюрации и т.п. Поскольку решение обобщенной ОЗВБ ведется для условий температуры заряда 15, а АО эксплуатируется до температур -50С, то для обеспечения полноты сгорания порохового заряда при минусовых температурах необходимо выбирать величину в соответствии с рекомендациями в табл.5 . Если текущий расчетный вариант в табл.3 не удовлетворяет ТЗ и поставленным ограничениям, производится корректировка предыдущего варианта за счет изменения величины максимального давления (колонка 2), веса заряда (столбцы 3 и 5), либо плотности заряжания (столбец 4). Возможно одновременное варьирование двумя или тремя параметрами (колонки 2-5 по отношению к столбцу 1). В таб. 6 приведен характер изменения анализируемых параметров при увеличении Таблица 6  Прямая задача внутренней баллистики. При выборе решения, удовлетворяющего ТЗ, производится автоматический переход к прямой задаче внутренней баллистики (ПЗВБ), в процессе решения которой рассчитываются кривые давлений газа и скорости снаряда при трех характерных температурах заряда 15, 50 и -50 (температурный градиент равен 100), либо при любых других. ПЗВБ решается путем численного интегрирования методом Рунге-Кутта системы баллистических уравнений. Решение обобщенной ОЗВБ и затем ПЗВБ осуществляется с помощью пакета программ КОБРА (КОмпьютерные Баллистические РAсчеты). Файл pri.dan имеет структуру, представленную в табл. 2.7. Данные по пороху для рассматриваемого примера приведены в табл.2.8. При решении ПЗВБ расчеты проводятся для трех температур окружающей среды 15, 50 и -50. Таблица 2.7.  Таблица 2.8.  Ввод необходимой температуры осуществляется по запросу ЭВМ. Результаты расчета отражаются в документальной или графической форме. На рис.2. показаны кривые изменения среднебаллистических давлений по длине канала ствола для трех характерных проектных температур порохового заряда: 50, 15 и -50 .  Рис.2. Кривые баллистических давлений по длине канала ствола для различных температур порохового заряда Расчет давлений при температурах, отличающихся от нормальной (15), производился с учетом влияния температуры заряда на импульс горения и силу пороха по зависимостям: Наличие кривых давлений для трех температур заряда позволяет построить кривую давлений пороховых газов на стенки ствола. Для этого, прежде всего, необходимо построить огибающую давлений. Необходимость ее построения обусловлена тем, что при различных температурах заряда наибольшие давления будут формироваться на различных участках по длине ствола. Максимальная нагрузка от давлений при температуре +50 будет приходиться на левую часть ствола, при +15 - на среднюю и при -50 - на переднюю (дульную) часть ствола (см. рис.2). Построение огибающей давлений проводится с учетом возможного случайного смещения положения точки максимального давления при температуре +50 при эксплуатации орудия. Накопленный опыт по эксплуатации артиллерийских орудий показывает, что такое смещение должно проводиться в сторону дульного среза на 1,5-2 калибра (точка c на рис.2.). Смещение в сторону казенной части не имеет смысла учитывать, так как в этом случае потери прочности ствола не происходит в силу того, что здесь труба подкрепляется такой весьма массивной деталью АО, как казенник. На рис.2.3 огибающая давлений газов - это кривая 4. После этого по формуле 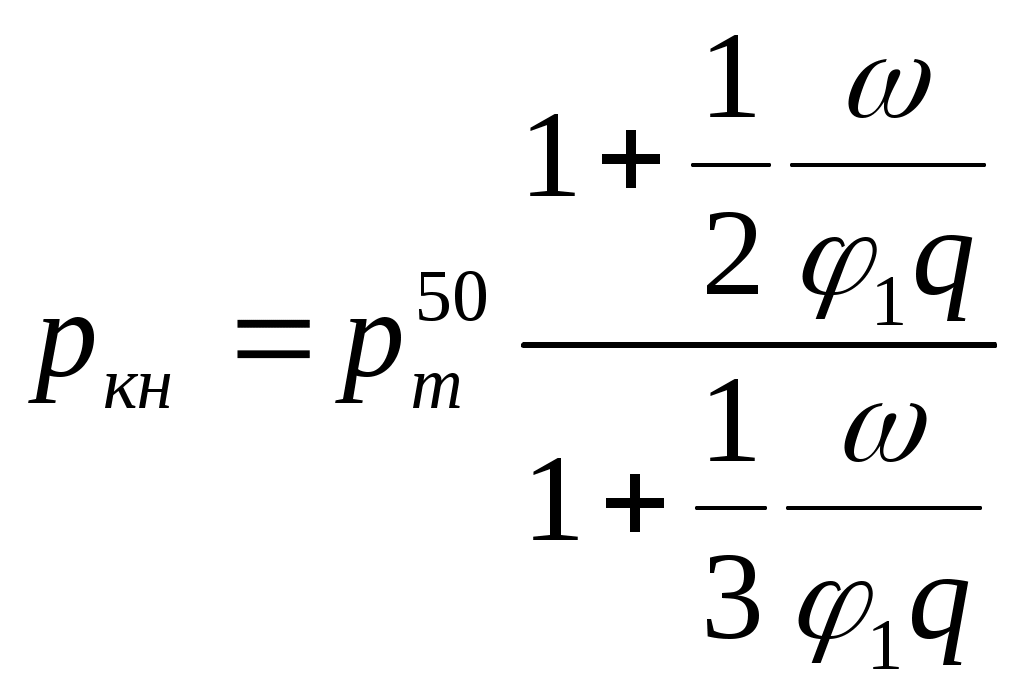 . Полученная кривая в дальнейшем используется для расчета прочности стенок ствола и определения его наружной конфигурации. . Полученная кривая в дальнейшем используется для расчета прочности стенок ствола и определения его наружной конфигурации.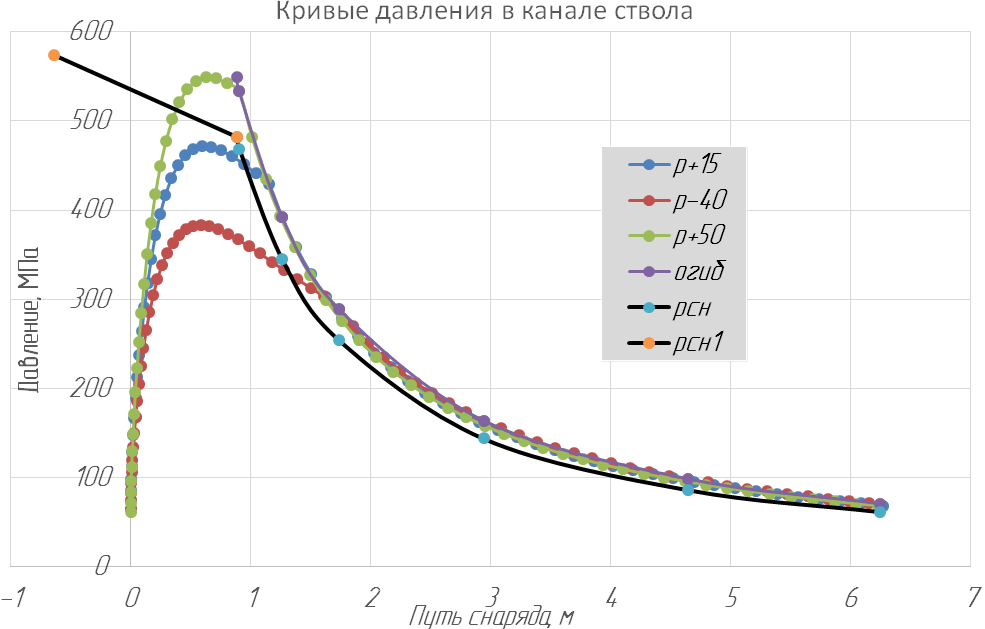 |
