Построение эмпирических формул методом наименьших квадратов. Работа содержит 39 страниц, 2 таблицы, 26 рисунков
 Скачать 485.31 Kb. Скачать 485.31 Kb.
|
АннотацияДанная курсовая работа проведена для нахождения на основе эмпирических данных аппроксимирующих формул, которые лучше всего описывают наши исходные данные. Расчёты проводились тремя способами: с помощью табличного редактора Microsoft Excel, при помощи MathCad, Matlab, а также VBA Exсel. Пояснительная записка выполнена на компьютере в текстовом редакторе Microsoft Word. Работа содержит 39 страниц, 2 таблицы, 26 рисунков. Abstract This course work was carried out to find approximating formulas based on empirical data that best describe our initial data. Calculations were carried out in three ways: using the Microsoft Excel spreadsheet editor, using MathCad, Matlab, and VBA Excel. The explanatory note is made on a computer in a Microsoft Word text editor. The report contains 36 pages, 2 tables, 26 figures. СОДЕРЖАНИЕАннотация 1 Введение 3 Глава 1. Построение эмпирических формул методом наименьших квадратов 4 1.1 Суть аппроксимации методом наименьших квадратов 4 1.2 Линейная аппроксимация 5 1.3 Квадратичная аппроксимация 5 1.4 Экспоненциальная аппроксимация 5 Глава 2. Элементы теории корреляции 7 2.1 Коэффициент корреляции 7 2.2 Коэффициент детерминированности 7 Глава 3. Аппроксимация заданных значений 9 3.1Линейная аппроксимация 9 MS Excel 9 MathCad 11 Пример на VBA 13 MATLAB 22 3.2Квадратичная аппроксимация 23 MS Excel 23 MathCad 25 Пример на VBA 26 MATLAB 27 3.3Экспоненциальная аппроксимация 28 MS Excel 28 MathCad 30 Пример на VBA 31 MATLAB 32 3.4 Выбор наиболее подходящей аппроксимации 34 Заключение 35 Вывод 36 Библиографический список 37 Введение Информатика – наука, которая рассматривает информационные, информационно-логические аспекты системного анализа и системные аспекты информационных процессов, информационно-динамические инварианты этих процессов. Из этого можно сделать вывод, что в рамках данного определения можно выделить структуризацию, систематизацию, корреляцию и упрощение определённых массивов данных в любой сфере деятельности человека. В общем виде это представляет собой системный подход, который позволяет оптимизировать работу с помощью вычислительной техники и соответствующих программ. Аппроксимация (от лат. "approximare" - "приближаться") - приближённое выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов, так как она позволяет выявить истинную зависимость полученных данных, учитывая погрешности различного рода, в результате можно выявить основную тенденцию зависимости (тренд), как результат получается определённая функциональная зависимость между значениями аргумента и корреляционным значением функции. Глава 1. Построение эмпирических формул методом наименьших квадратов Метод наименьших квадратов - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределённых систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределённых) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Суть аппроксимации методом наименьших квадратовЗадача заключается в нахождении коэффициентов линейной (квадратичной, экспоненциальной) зависимости, при которых функция переменных а1, а2 …am принимает наименьшее значение. То есть, при данных а1, а2, … am сумма квадратов отклонений экспериментальных данных от найденной прямой (кривой) будет наименьшей. В этом вся суть метода наименьших квадратов. Математически выражается следующим образом:
где S – минимум функции при заданных значениях 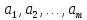 . .Таким образом задача по определению коэффициентов ai сводится к нахождению минимума функции S, определяемой формулой (1). Для этого требуется решить следующую систему уравнений (2).
Конкретный вид системы дифференциальных уравнений в частных производных (2) зависит от того, из какого класса эмпирических формул мы ищем зависимость. В нашем случае это линейная, квадратичная и экспоненциальная функции. Линейная аппроксимацияВ случае линейной функции 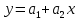 система (2) примет следующий вид: система (2) примет следующий вид:
Квадратичная аппроксимацияВ случае квадратичной зависимости 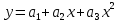 система (2) примет следующий вид: система (2) примет следующий вид:
Экспоненциальная аппроксимацияВ случае экспоненциальной зависимости
Сначала следует линеаризовать функцию – свести к линейной. Для этого логарифмируем левую и правую часть равенства, после чего получаем следующее соотношение:
Обозначим lny и lna1 соответственно через t и c, тогда зависимость (5) может быть записана в виде t = a1+ a2x, что позволяет применить формулы (3) с заменой a1 на c и yi на ti. Глава 2. Элементы теории корреляцииГрафик, который получится после нахождения коэффициентов а1, а2…am, максимально близко приближен к заданным значениям функции, но все же не совпадает с ними. Чтобы определить какой вид аппроксимации подходит лучше всего, вводится понятие коэффициента корреляции и детерминированности. 2.1 Коэффициент корреляцииКоэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой. Коэффициент корреляции вычисляется по формуле:
где 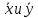 среднее арифметическое значение соответственно по x и y. среднее арифметическое значение соответственно по x и y.Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе |ρ| к 1, тем теснее линейная связь между x и y. Если коэффициент корреляции существенно меньше 1, это не означает отсутствие зависимости между параметрами x и y. Возможно, следует найти иные виды аппроксимации, которые отличны от той, что использовалась. 2.2 Коэффициент детерминированностиЧтобы выяснить насколько точно построенная кривая отражает эмпирические данные вводится еще одна характеристика - коэффициент детерминированности. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности, который показывает, насколько точно уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями функции. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений функции. Коэффициент детерминированности находится по следующей формуле:
где 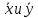 среднее арифметическое значение соответственно по x и y. среднее арифметическое значение соответственно по x и y.Глава 3. Аппроксимация заданных значенийДля начала оформим таблицу заданных значений (таблица 1). Таблица 1 – Заданные значения X и Y
Линейная аппроксимацияMS ExcelДля аппроксимации в MS Excel нужно внести данные в таблицу. Значения Y помещены в ячейки A2:A15. Значения X помещены в ячейки B2:B25. Для нахождения функции регрессии требуется решить систему (3). Система будет иметь вид:
Так как Excel программа для работы с электронными таблицами, посчитаем значения сумм в системе. Функция СУММ суммирует значения, воспользуемся ей: 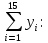 A16 = СУММ(А1:А15), в ячейке A16 появилось значение 389 . A16 = СУММ(А1:А15), в ячейке A16 появилось значение 389 . 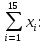 В16 = СУММ(В1:В15), в ячейке В26 появилось значение 216. Теперь необходимо возвести все значения X во вторую степень, для этого запишем формулу в ячейку C2 = B2^2. И протянем эту формулу до 15 строки включительно. 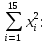 C16 = СУММ(C1:C15), в ячейке C16 появилось значение 4496. Следующим шагом находим произведение X и Y, для этого запишем формулу в ячейку D2 = A2*B2. И протянем эту формулу до 15 строки включительно. 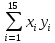 D16 = СУММ(D1:D15), в ячейке D16 появилось значение 3219,12. Теперь система (3) приняла вид: 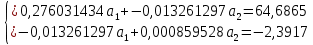 Решим эту систему матричным методом с помощью MS Excel: 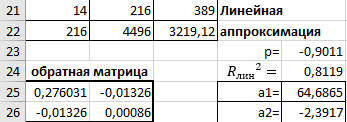 Рисунок 1-Линейная аппроксимация На рисунке 1 в ячейках A25:B26 записана формула {=МОБР(A21:B22)}. В ячейках E25:E26 записана формула {=МУМНОЖ(A25:B26,C21:C22)}. Получили значения a1 и а2, равные 64,6865 и -2,3917 соответственно. Значит, функция линейной регрессии исходных значений будет иметь следующий вид: 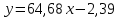 Проверим правильность нахождения формулы линии тренда, для этого изобразим наши точки на графике и аппроксимируем их с помощью механизмов MS Excel (рисунок 2) 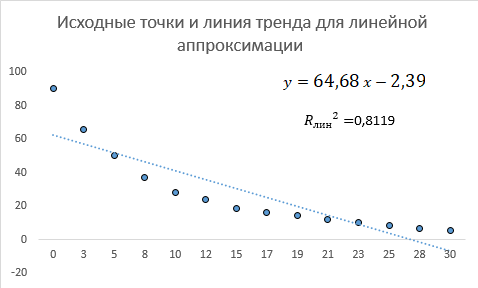 Рисунок 2-Исходные точки и линия тренда для линейной аппроксимации Убедились в том, что уравнение линии тренда совпадает с полученным нами. С помощью равенств (7) и (8) найдем значение коэффициента корреляции и детерминированности, предварительно посчитав все необходимые значения с помощью MS Excel. 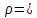 -0,9011 -0,9011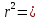 0,8119 0,8119Еще раз убеждаемся в правильности наших расчетов, сравнивая наши значения коэффициента детерминированности и полученные значения с помощью MS Excel (рисунок 2). MathCadЗапишем исходные данные в матрицы (рисунок 3).  Рисунок 3- исходные данные в MathCad Начало нумерации элементов в векторах и матрицах определяется встроенной переменной ORIGIN. По умолчанию ORIGIN=0, то есть первый элемент вектора, первая строка и первый столбец матрицы имеют индекс ноль. Для дальнейшего удобства устанавливаем ORIGIN=1. Далее решаем систему (3) с помощью оператора line. Перед этим задаем значения n – количество значений X и Y. (рисунок 4). 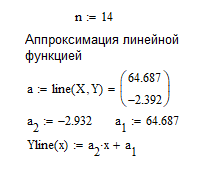 Рисунок 4- Вычисления в MathCad Были найдены аналогичные значения а1 и а2, как и с помощью программы MS Excel. Построим график, предварительно задав шаг x, также посчитаем коэффициент корреляции и детерминированности (рисунок 5). 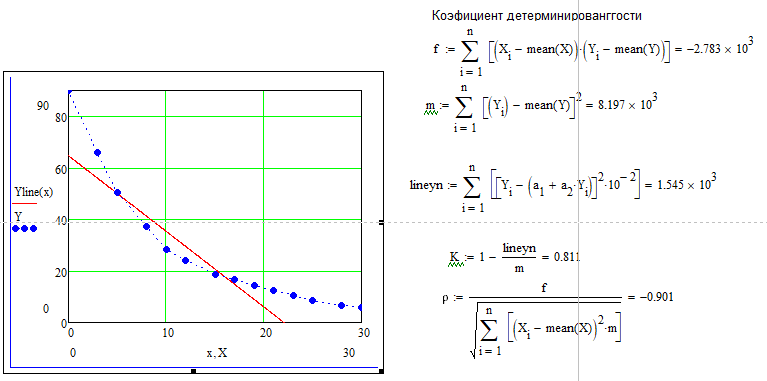 Рисунок 5- Результат для линейной аппроксимации На рисунке 5, видим, что коэффициент корреляции и детерминированности полностью совпадают с значениями полученными в MS Excel. Однако стоит отметить удобство нахождения этих коэффициентов в Mathcad – программа позволяет напрямую искать значения, без предварительного нахождения разнообразных сумм и произведений, требующихся в формулах. Пример на VBAДля вычислений написан следующий код (Рисунки 6-8). Option Explicit Dim Inp_Data As String Dim FileName As String Public UR As Range, CL As Range Dim R1 As Byte, C1 As Byte, R As Byte Dim i As Integer, j As Integer, k As Integer Public n As Integer Dim m_1() As Single, m_2() As Single Public X() As Single, Y() As Single Public lny() As Single Const n1 = 2 Public Ftab(1 To n1) As Single Public Stab(1 To n1) As Single Public alfa As Single Public stl() As Single, ssrl() As Single, stsqr() As Single, ssrsqr() As Single, YL() As Single, Ysqr() As Single, Yexp() As Single, lnYexp() As Single Public Sx As Single, Sy As Single, Sxy As Single, Sx2 As Single, Sx3 As Single, Sx4 As Single, Sx2y As Single, Sx2sr As Single, Sy2sr As Single, Sxysr As Single, Slny As Single, Sxlny As Single Public a1L As Single, a2L As Single, koef_cor As Single, MD As Single Public Sa1L As Single, Sa2L As Single, Xsr As Single, Ysr As Single, lnYsr As Single Public SostL As Single, SregrL As Single, SpolnL As Single, R_det_L As Single Public Fline As Single, Sline As Single, ta1L As Single, ta2L As Single Public a1sqr As Single, a2sqr As Single, a3sqr As Single Public Sa1sqr As Single, Sa2sqr As Single, Sa3sqr As Single Public Sostsqr As Single, Sregrsqr As Single, Spolnsqr As Single, R_det_sqr As Single, DSost As Single Public Fsqr As Single, Ssqr As Single, ta1sqr As Single, ta2sqr As Single, ta3sqr As Single Public cexp As Single, a1exp As Single, a2exp As Single Public Sa1exp As Single, Sa2exp As Single Public Sostexp As Single, Sregrexp As Single, Spolnexp As Single, R_det_exp As Single Public Fexp As Single, ta1exp As Single, ta2exp As Single Public gr As Integer Public Min As Single, Max As Single, Xpr As Single, Ypr As Single Public f_st As String Sub Êíîïêà1_Ùåë÷îê() n = 0 ReadList UserForm1.Show End Sub Public Sub ReadList() Sheets("VBA").Activate Set UR = ActiveSheet.UsedRange R1 = UR.Rows(1).Row If R1 = 0 Then Exit Sub C1 = UR.Columns(1).Column n = 0 Cells(R1, C1).Activate While ActiveCell <> "" If IsNumeric(ActiveCell.Value) Then n = n + 1 ReDim Preserve m_1(1 To 2, 1 To n) m_1(1, n) = ActiveCell.Value m_1(2, n) = ActiveCell.Offset(0, 1).Value End If ActiveCell.Offset(1, 0).Activate Wend If n > 0 Then ReDim m_2(1 To n, 1 To 2) For j = 1 To n m_2(j, 1) = m_1(1, j) m_2(j, 2) = m_1(2, j) Next j Else ReDim m_2(1 To 1, 1 To 2) End If With UserForm1.ListBox1 .ColumnCount = 2 .List = m_2 End With End Sub Public Sub Read_XY(X, Y) ReDim X(1 To n) ReDim Y(1 To n) For j = 1 To n X(j) = m_2(j, 1) Y(j) = m_2(j, 2) Next j End Sub Public Sub Read_tabl(alfa) Dim d_f1 As Integer, d_f2 As Integer d_f1 = 1 d_f2 = n - 1 On Error GoTo old_func Ftab(1) = WorksheetFunction.F_Inv_RT(alfa, d_f1, d_f2 - 1) Ftab(2) = WorksheetFunction.F_Inv_RT(alfa, d_f1, d_f2 - 2) Stab(1) = WorksheetFunction.T_Inv_2T(alfa, d_f2) Stab(2) = WorksheetFunction.T_Inv_2T(alfa, d_f2 - 1) Exit Sub old_func: Ftab(1) = WorksheetFunction.FInv(alfa, d_f1, d_f2 - 1) Ftab(2) = WorksheetFunction.FInv(alfa, d_f1, d_f2 - 2) Stab(1) = WorksheetFunction.TInv(alfa, d_f2) Stab(2) = WorksheetFunction.TInv(alfa, d_f2 - 1) End Sub Public Sub L_Kram(a11 As Integer, a12 As Single, a21 As Single, a22 As Single, b1 As Single, b2 As Single, a1 As Single, a2 As Single) Dim d As Single, d1 As Single, d2 As Single d = a11 * a22 - a21 * a12 d1 = b1 * a22 - b2 * a12 d2 = a11 * b2 - a21 * b1 a1 = d1 / d a2 = d2 / d End Sub Public Sub Sqr_Kram(a11 As Integer, a12 As Single, a13 As Single, a21 As Single, a22 As Single, a23 As Single, a31 As Single, a32 As Single, a33 As Single, b1 As Single, b2 As Single, b3 As Single, a1 As Single, a2 As Single, a3 As Single, MD As Single) Dim d As Single, d1 As Single, d2 As Single, d3 As Single d = a11 * a22 * a33 + a12 * a23 * a31 + a21 * a32 * a13 - a13 * a22 * a31 - a21 * a12 * a33 - a11 * a23 * a32 d1 = b1 * a22 * a33 + a12 * a23 * b3 + b2 * a32 * a13 - a13 * a22 * b3 - b2 * a12 * a33 - b1 * a23 * a32 d2 = a11 * b2 * a33 + b1 * a23 * a31 + a21 * b3 * a13 - a13 * b2 * a31 - a21 * b1 * a33 - a11 * a23 * b3 d3 = a11 * a22 * b3 + a12 * b2 * a31 + a21 * a32 * b1 - b1 * a22 * a31 - a21 * a12 * b3 - a11 * b2 * a32 a1 = d1 / d a2 = d2 / d a3 = d3 / d MD = d End Sub Public Sub Koef_det(ns As Integer, a() As Single, b() As Single, c As Single, s1 As Single, s2 As Single, s3 As Single, R As Single) Dim i As Integer For i = 1 To ns s1 = s1 + (b(i) - a(i)) ^ 2 s2 = s2 + (b(i) - c) ^ 2 Next i s3 = s1 + s2 R = 1 - s1 / s3 End Sub Public Sub ZnachLine(n As Integer, DS As Single, R2 As Single, a As Single, asr As Single, a1 As Single, a2 As Single, s1 As Single, s2 As Single, f As Single, t1 As Single, t2 As Single) s1 = Sqr(DS * a / (n * (n - 2) * asr)) s2 = Sqr(DS / ((n - 2) * asr)) f = R2 * (n - 2) / (1 - R2) t1 = Abs(a1) / s1 t2 = Abs(a2) / s2 End Sub Public Sub MinMax(a() As Single, n As Integer, Min As Single, Max As Single) Dim i As Integer Min = a(1) Max = a(1) For i = 2 To n If a(i) > Max Then Max = a(i) If a(i) < Min Then Min = a(i) Next i End Sub Public Sub Print_rez(gr As Integer, sa1 As String, sa2 As String, sa3 As String, sk As String, sR As String, sm1 As String, sm2 As String, sm3 As String, sf As String, st1 As String, st2 As String, st3 As String, a1 As Single, a2 As Single, a3 As Single, k As Single, R As Single, m1 As Single, m2 As Single, m3 As Single, f As Single, t1 As Single, t2 As Single, t3 As Single) Dim Fd As Single, Sd As Single, st As String, str1 As String f_st = "0.0000" If gr = 2 Then Fd = Ftab(2) Else Fd = Ftab(1) If gr = 2 Then Sd = Stab(2) Else Sd = Stab(1) Select Case gr Case 1 st = "ëèíåéíîé àïïpîêñèìàöèè" With UserForm1 .tb_k1l = Format(a1, f_st) .tb_k2l = Format(a2, f_st) .tb_kc = Format(k, "0.000000") .tb_kdl = Format(R, "0.000000") .tb_k1l_s = Format(m1, "0.000000") .tb_k2l_s = Format(m2, "0.000000") .tb_k1l_tr = Format(t1, f_st) .tb_k2l_tr = Format(t2, f_st) .tb_kl_tt = Format(Sd, f_st) .tb_l_ft = Format(Fd, f_st) .tb_l_fr = Format(f, f_st) If t1 > Sd Then .tb_k1l_z = "çíà÷èì" Else .tb_k1l_z = "íå çíà÷èì" End If If t2 > Sd Then .tb_k2l_z = "çíà÷èì" Else .tb_k2l_z = "íå çíà÷èì" End If If f > Fd Then .tb_l_z = "çíà÷èìî" Else .tb_l_z = "íå çíà÷èìî" End With Case 2 st = "êâàäpàòè÷íîé àïïpîêñèìàöèè" With UserForm1 .tb_k1q = Format(a1, f_st) .tb_k2q = Format(a2, f_st) .tb_k3q = Format(a3, f_st) .tb_kdq = Format(R, "0.000000") .tb_k1q_s = Format(m1, "0.000000") .tb_k2q_s = Format(m2, "0.000000") .tb_k3q_s = Format(m3, "0.000000") .tb_k1q_tr = Format(t1, f_st) .tb_k2q_tr = Format(t2, f_st) .tb_k3q_tr = Format(t3, f_st) .tb_kq_tt = Format(Sd, f_st) .tb_q_ft = Format(Fd, f_st) .tb_q_fr = Format(f, f_st) If t1 > Sd Then .tb_k1q_z = "çíà÷èì" Else .tb_k1q_z = "íå çíà÷èì" End If If t2 > Sd Then .tb_k2q_z = "çíà÷èì" Else .tb_k2q_z = "íå çíà÷èì" End If If t3 > Sd Then .tb_k3q_z = "çíà÷èì" Else .tb_k3q_z = "íå çíà÷èì" End If If f > Fd Then .tb_q_z = "çíà÷èìî" Else .tb_q_z = "íå çíà÷èìî" End With Case 3 st = "ýêñïîíåíöèàëüíîé àïïpîêñèìàöèè" With UserForm1 .tb_k1e = Format(a1, f_st) .tb_k2e = Format(a2, f_st) .tb_kde = Format(R, "0.000000") .tb_k1e_s = Format(m1, "0.000000") .tb_k2e_s = Format(m2, "0.000000") .tb_k1e_tr = Format(t1, f_st) .tb_k2e_tr = Format(t2, f_st) .tb_ke_tt = Format(Sd, f_st) .tb_e_ft = Format(Fd, f_st) .tb_e_fr = Format(f, f_st) If t1 > Sd Then .tb_k1e_z = "çíà÷èì" Else .tb_k1e_z = "íå çíà÷èì" End If If t2 > Sd Then .tb_k2e_z = "çíà÷èì" Else .tb_k2e_z = "íå çíà÷èì" End If If f > Fd Then .tb_e_z = "çíà÷èìî" Else .tb_e_z = "íå çíà÷èìî" End With End Select R1 = ActiveSheet.UsedRange.Row + _ ActiveSheet.UsedRange.Rows.Count + 1 Cells(R1, C1).Activate If gr = 1 Then ActiveCell = "N=" + Str(n) + " - ÷èñëî íàáëþäåíèé" ActiveCell.Offset(1, 0).Activate ActiveCell = "Òàáëè÷íûå çíà÷åíèÿ êðèòåðèåâ:" ActiveCell.Offset(1, 0).Activate ActiveCell = "Ôèøåðà Ñòüþäåíòà" ActiveCell.Offset(1, 0).Activate ActiveCell = Format(Ftab(1), "0.0000") + Space(8) + Format(Stab(1), "0.0000") + " - ïðè âû÷èñëåíèè äâóõ êîýôôèöèåíòîâ" ActiveCell.Offset(1, 0).Activate ActiveCell = Format(Ftab(2), "0.0000") + Space(8) + Format(Stab(2), "0.0000") + " - ïðè âû÷èñëåíèè òðåõ êîýôôèöèåíòîâ" ActiveCell.Offset(1, 0).Activate End If str1 = sa1 + "=" + Format(a1, f_st) + " " + sa2 + "=" + Format(a2, f_st) If gr = 2 Then str1 = str1 + " " + sa3 + "=" + Format(a3, f_st) End If ActiveCell = str1 + " -êîýôôèöèåíòû " + st ActiveCell.Offset(1, 0).Activate If gr = 1 Then ActiveCell = sk + Format(k, "0.000000") + " -êîýôôèöèåíò êîppåëÿöèè" End If ActiveCell.Offset(1, 0).Activate ActiveCell = sR + Format(R, "0.000000") + " -êîýôôèöèåíò äåòåpìèíèpîâàííîñòè" ActiveCell.Offset(1, 0).Activate str1 = sm1 + Format(m1, "0.000000") + " " + sm2 + Format(m2, "0.000000") If gr = 2 Then str1 = str1 + " " + sm3 + Format(m3, f_st) + " -ñòàíäàpòíûå îøèáêè êîýôôèöèåíòîâ " End If ActiveCell = str1 ActiveCell.Offset(1, 0).Activate ActiveCell = "Êpèòåpèè äëÿ ïpîâåpêè íóëåâûõ ãèïîòåç " ActiveCell.Offset(1, 0).Activate str1 = sf + Format(f, f_st) + " " + st1 + Format(t1, f_st) + " " + st2 + Format(t2, f_st) If gr = 2 Then str1 = str1 + " " + st3 + Format(t3, f_st) End If ActiveCell = str1 ActiveCell.Offset(1, 0).Activate If f > Fd Then ActiveCell = "Ópàâíåíèå " + st + " çíà÷èìî" Else ActiveCell = "Ópàâíåíèå " + st + " íå çíà÷èìî" End If ActiveCell.Offset(1, 0).Activate If t1 > Sd Then ActiveCell = "Êîýôôèöèåíò " + sa1 + " çíà÷èì" Else ActiveCell = "Êîýôôèöèåíò " + sa1 + " íå çíà÷èì" End If ActiveCell.Offset(1, 0).Activate If t2 > Sd Then ActiveCell = "Êîýôôèöèåíò " + sa2 + " çíà÷èì" Else ActiveCell = "Êîýôôèöèåíò " + sa2 + " íå çíà÷èì" End If ActiveCell.Offset(1, 0).Activate If gr = 2 Then If t3 > Sd Then ActiveCell = "Êîýôôèöèåíò " + sa3 + " çíà÷èì" Else ActiveCell = "Êîýôôèöèåíò " + sa3 + " íå çíà÷èì" End If End If ActiveCell.Offset(1, 0).Activate End Sub Public Sub graf() Dim cell_1 As String, cell_2 As String R1 = ActiveSheet.UsedRange.Row + ActiveSheet.UsedRange.Rows.Count + 1 For i = 1 To n Cells(R1 + i - 1, 1) = X(i) Cells(R1 + i - 1, 2) = a1L + a2L * X(i) Next i cell_1 = Cells(R1, 1).Address cell_2 = Cells(R1 + n - 1, 2).Address ActiveSheet.Shapes.AddChart.Select ActiveChart.ChartType = xlXYScatterSmoothNoMarkers ActiveChart.SetSourceData Source:=Range(cell_1 + ":" + cell_2) ActiveChart.SeriesCollection.NewSeries cell_1 = Cells(UR.Row + 1, UR.Column).Address cell_2 = Cells(UR.Row + n - 1, UR.Column).Address ActiveChart.SeriesCollection(2).XValues = Range(cell_1 + ":" + cell_2) ActiveChart.SeriesCollection(2).Values = Range(Cells(UR.Row + 1, UR.Column + 1).Address + ":" + Cells(UR.Row + n - 1, UR.Column + 1).Address) ActiveChart.SeriesCollection(2).Select ActiveChart.SeriesCollection(2).ChartType = xlXYScatter ActiveChart.SetElement (msoElementChartTitleAboveChart) Selection.Caption = "Ëèíåéíàÿ" ActiveSheet.ChartObjects(1).Left = 430 For i = 1 To n Cells(R1 + i - 1, 3) = a1sqr + a2sqr * X(i) + a3sqr * X(i) * X(i) Next i cell_1 = Cells(R1, 1).Address cell_2 = Cells(R1 + n - 1, 3).Address ActiveSheet.Shapes.AddChart.Select ActiveChart.ChartType = xlXYScatterSmoothNoMarkers ActiveChart.SeriesCollection.NewSeries ActiveChart.SeriesCollection(1).XValues = Range(cell_1 + ":" + Cells(R1 + n - 1, 1).Address) ActiveChart.SeriesCollection(1).Values = Range(Cells(R1, 3).Address + ":" + cell_2) ActiveChart.SeriesCollection.NewSeries ActiveChart.SeriesCollection(2).XValues = Range(Cells(UR.Row + 1, UR.Column).Address + ":" + Cells(UR.Row + n - 1, UR.Column).Address) ActiveChart.SeriesCollection(2).Values = Range(Cells(UR.Row + 1, UR.Column + 1).Address + ":" + Cells(UR.Row + n - 1, UR.Column + 1).Address) ActiveChart.SeriesCollection(2).Select ActiveChart.SeriesCollection(2).ChartType = xlXYScatter ActiveChart.SetElement (msoElementChartTitleAboveChart) Selection.Caption = "Êâàäðàòè÷íàÿ" ActiveSheet.ChartObjects(2).Left = 800 On Error Resume Next ActiveChart.SeriesCollection(3).Delete On Error GoTo 0 For i = 1 To n Cells(R1 + i - 1, 4) = a1exp * Exp(a2exp * X(i)) Next i cell_1 = Cells(R1, 1).Address cell_2 = Cells(R1 + n - 1, 4).Address ActiveSheet.Shapes.AddChart.Select ActiveChart.ChartType = xlXYScatterSmoothNoMarkers ActiveChart.SeriesCollection.NewSeries ActiveChart.SeriesCollection(1).XValues = Range(cell_1 + ":" + Cells(R1 + n - 1, 1).Address) ActiveChart.SeriesCollection(1).Values = Range(Cells(R1, 4).Address + ":" + cell_2) ActiveChart.SeriesCollection.NewSeries ActiveChart.SeriesCollection(2).XValues = Range(Cells(UR.Row + 1, UR.Column).Address + ":" + Cells(UR.Row + n - 1, UR.Column).Address) ActiveChart.SeriesCollection(2).Values = Range(Cells(UR.Row + 1, UR.Column + 1).Address + ":" + Cells(UR.Row + n - 1, UR.Column + 1).Address) ActiveChart.SeriesCollection(2).Select ActiveChart.SeriesCollection(2).ChartType = xlXYScatter ActiveChart.SetElement (msoElementChartTitleAboveChart) Selection.Caption = "Ýêñïîíåíöèàëüíàÿ" ActiveSheet.ChartObjects(3).Left = 1170 On Error Resume Next ActiveChart.SeriesCollection(3).Delete On Error GoTo 0 End Sub Зададим исходные данные (Рисунок 9).  Рисунок 9.- Исходные данные в примере на VBA После проведённых вычислений в самой программе мы узнаём результат линейной аппроксимации. 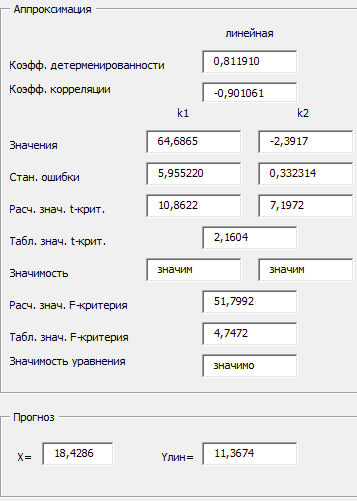 Рисунок 10- Результатылинейной аппроксимации в примере на VBA На рисунке 10, видим, что коэффициент корреляции и детерминированности полностью совпадают со значениями, полученными в MS Excel. Однако стоит отметить удобство нахождения этих коэффициентов в VBA – программа позволяет упорядочить полученные данные, скрывая все вычисления. MATLABДля этой программы был написан код (Рисунок 21). 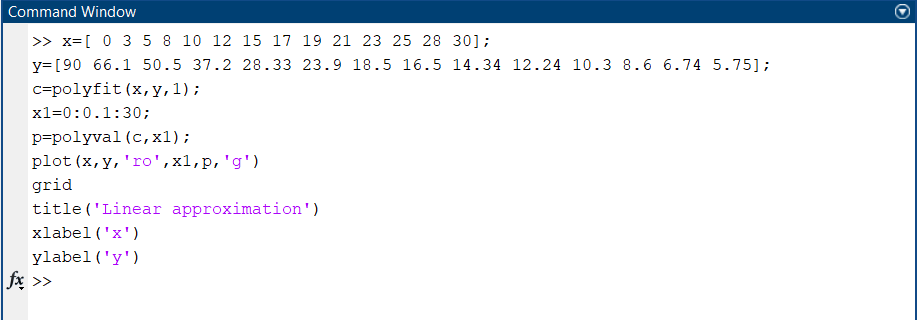 Рисунок 21- Кол для программы MATLAB После чего программа строит график , который полностью совпадает с построенными нами графиками ранее. Что доказывает правильность нашего решения. 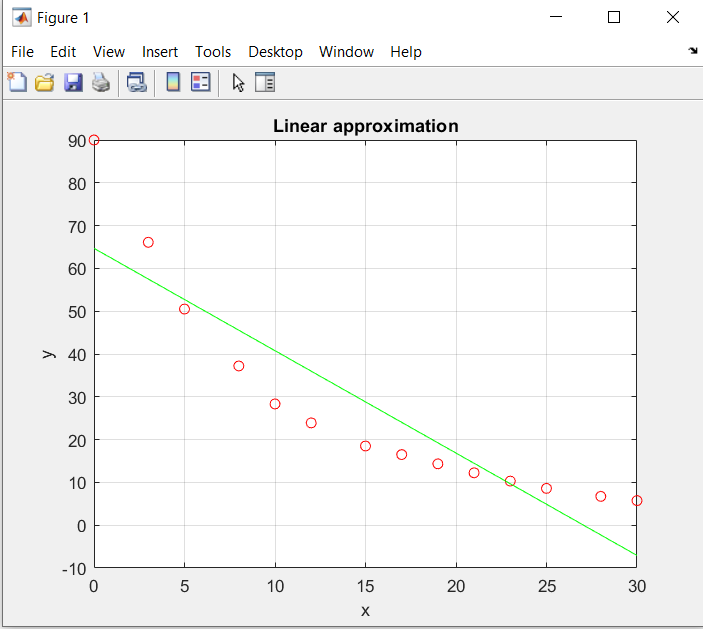 Рисунок 22- Результат в программе MATLAB для линейной аппроксимации Квадратичная аппроксимацияMS ExcelДля аппроксимации квадратичной функцией, следует выполнить аналогичные действия, только решать теперь придётся систему (4), предварительно с помощью таблиц посчитав все значения. По окончании имеем следующую систему, аналогично решаем её матричным методом (рисунок 11). Система (4) приняла вид: 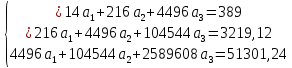 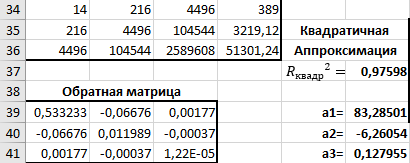 Рисунок 11- Квадратичная аппроксимация в MS Excel. Определив коэффициенты a1,a2 и а3 можем записать уравнение квадратичной аппроксимации: 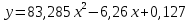 Проверим правильность нахождения формулы линии тренда, для этого изобразим наши точки на графике и аппроксимируем их с помощью механизмов MS Excel (рисунок 12). 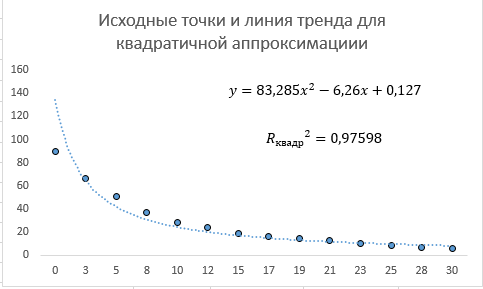 Рисунок 12- Исходные точки и линия тренда для квадратичной аппроксимации Очередной раз убедились в правильности своих вычислений, так как полученное нами уравнение аппроксимации совпадает с уравнением, полученным с помощью механизмов MS Excel. С помощью равенства (8) найдём значение коэффициента детерминированности, предварительно посчитав все необходимые значения с помощью MS Excel. 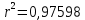 Еще раз убеждаемся в правильности наших расчетов, сравнивая наши значения коэффициента детерминированности и полученные значения с помощью MS Excel (рисунок 12). MathCadДля построения в Mathcad необходимо снова повторить матрицы (рисунок 3), либо делать все вычисления под линейной аппроксимацией, все необходимые переменные мы переопределим, ошибок у нас не возникнет. Решаем систему уравнения с помощью оператора genfit, определяем коэффициенты a1, a2 и a3. Единственное отличие от линейной аппроксимации заключается в системе. Теперь мы решаем систему (4) и определяем 3 переменные (рисунок 8).  Рисунок 13- Вычисления в MathCad Были найдены аналогичные значения переменных, как и с помощью программы MS Excel. Построим график, также посчитаем коэффициент детерминированности (рисунок 14). 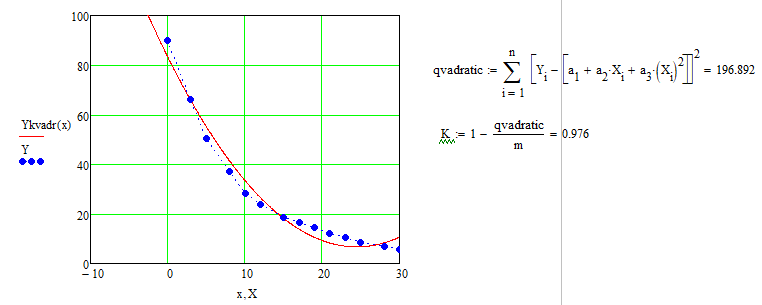 Рисунок 14- Результат для квадратичной аппроксимации Коэффициент детерминированности равен тому, что мы нашли в MS Excel. Подтверждаем правильность наших действий. Пример на VBAДанные уже находятся в программе. Повторного ввода не требуется. Смотрим на результаты. 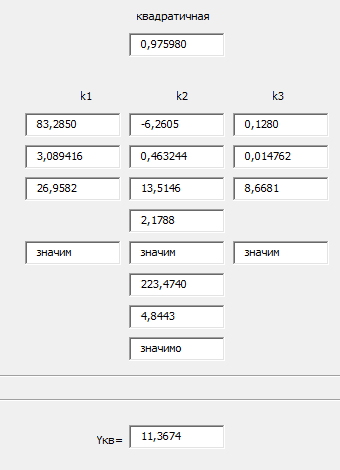 Рисунок 15- Результаты квадратичной аппроксимации в примере на VBA Еще раз убеждаемся в правильности наших расчетов, сравнивая наши значения коэффициента детерминированности. Убеждаемся в их схожести. Что лишний раз подтверждает правильность расчётов. MATLABПишем код для квадратичной аппроксимации (Рисунок 23). 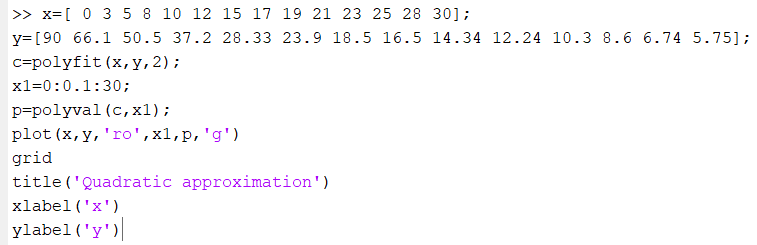 Рисунок 23- Код для программы MATLAB После выполнения данного кода, программа выдаёт нам график квадратичной аппроксимации (рисунок 24). График совпадает с ранее построенными графиками в других программах. Что доказывает верность результата. 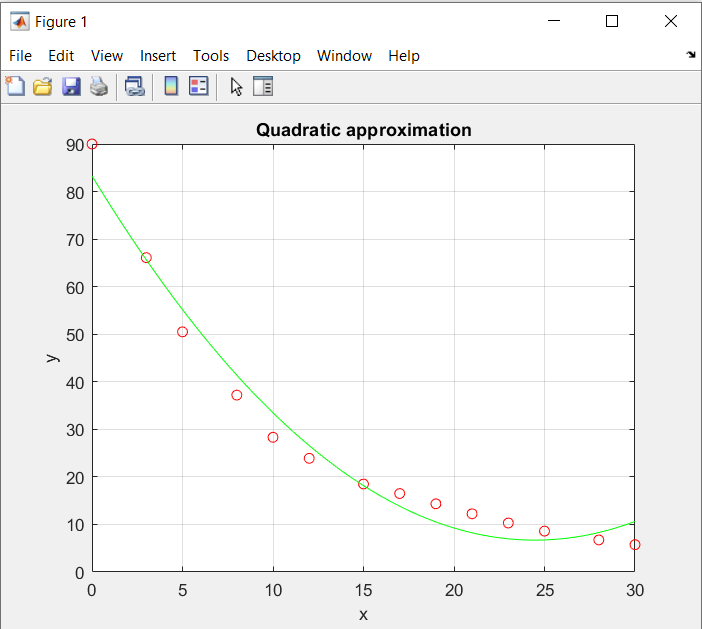 Рисунок 24- Результат в программе MATLAB для квадратичной аппроксимации Экспоненциальная аппроксимацияMS ExcelЭкспоненциальная аппроксимация отличается от предыдущих тем, что в уравнении (5) переменная a2 находится в степени экспоненты. Для решения такой логарифмируют левую и правую части уравнения (5) и получают уравнение (6). В MS Excel, чтобы прологарифмировать две части уравнения нужно вручную найти все логарифмы всех значений. И дальше работать с ними. После этих преобразований (линеаризации функции) можем воспользоваться системой (3), которая примет вид:
где с = ln(a1). Теперь система (3) приняла вид: 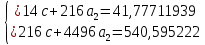 Решим эту систему матричным методом – получим коэффициенты a2 и с. Так как с = ln(a1), поместим формулу в ячейку E55 =EXP(E53), таким способом найдем коэффициенты a1 и а2 (рисунок 16). 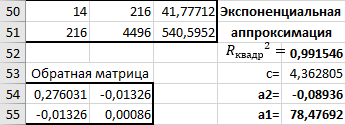 Рисунок 16- Экспоненциальная аппроксимация в MS Excel. После нахождения коэффициентов можем записать уравнения регрессии: 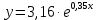 Проверим правильность нахождения формулы линии тренда, для этого изобразим наши точки на графике и аппроксимируем их с помощью механизмов MS Excel (рисунок 17) 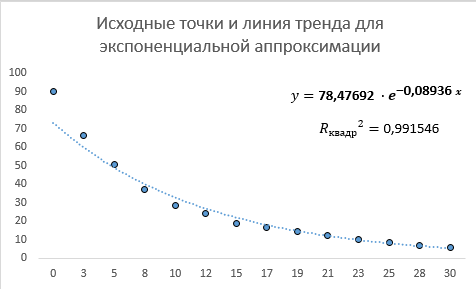 Рисунок 17- Исходные точки и линия тренда для экспоненциальной аппроксимации Уравнение линии тренда совпадает с полученным нами, различие заключается только в точности за счёт округления. Найдём коэффициент детерминированности по формуле (8). 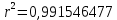 Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости 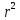 = 0,991546477 не совпадает с истинным значением = 0,991546477 не совпадает с истинным значением 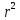 = 0, 0,8119 (это значение было сосчитано вручную выше) поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения yi, а преобразованные значения ln(yi) с дальнейшей линеаризацией. = 0, 0,8119 (это значение было сосчитано вручную выше) поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения yi, а преобразованные значения ln(yi) с дальнейшей линеаризацией.MathCadВ Mathcad проделываем такие же действия, как и для линейной и квадратичной аппроксимаций. Единственное различие, добавляется ещё одно действие для определения коэффициента a2 (рисунок 18).  Рисунок 18- Вычисления в MathCad Были найдены аналогичные значения переменных, как и с помощью программы MS Excel. Построим график, также посчитаем коэффициент детерминированности (рисунок 19). 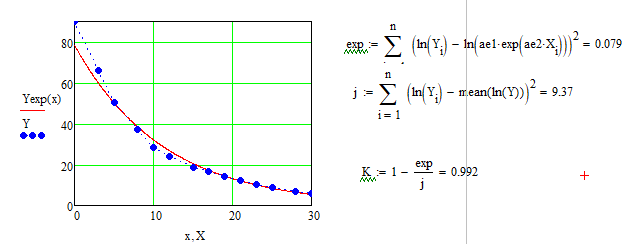 Рисунок 19- Результат для экспоненциальной аппроксимации Коэффициент детерминированности равен тому, что мы нашли в MS Excel. Подтверждаем правильность наших действий. Пример на VBAДанные уже находятся в программе. Повторного ввода не требуется. Смотрим на результаты (Рисунок 20). 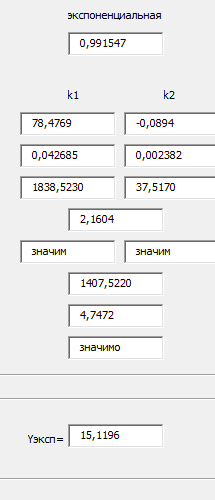 Рисунок 20- Результаты экспоненциальной аппроксимации в примере на VBA Еще раз убеждаемся в правильности наших расчетов, сравнивая наши значения коэффициента детерминированности. Убеждаемся в их схожести. Что лишний раз подтверждает правильность расчётов. MATLABПишем код для экспоненциальной аппроксимации (Рисунок 24).  Рисунок 25- Код для программы MATLAB После выполнения данного кода , программа выдаёт нам график экспоненциальной аппроксимации (рисунок 26). График совпадает с ранее построенными графиками в других программах. Что доказывает верность результата. 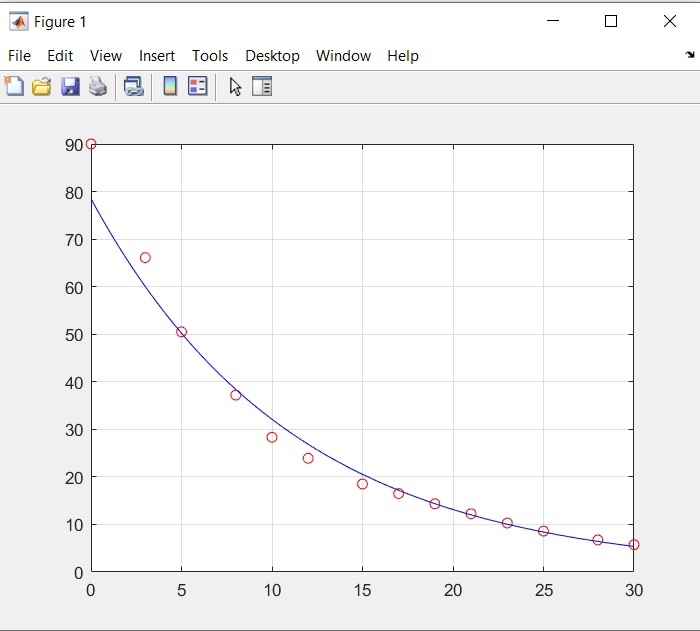 Речонок 26- Результат в программе MATLAB для экспоненциальной аппроксимации Аппроксимация данных производилась тремя способами, каждый из них максимально точно смог восстановить функцию регресса. Так как коэффициент корреляции мы находили только для линейной функции, стоит сравнивать точность функций регресса по коэффициентам детерминированности. Приведём полученные ранее коэффициенты детерминированности (таблица 2). Таблица 2- Результаты коэффициента детерминированности
Чем ближе значение коэффициента детерминированности к 1, тем меньше сумма остаточных квадратов, следовательно, тем ближе график прошел к нашим заданным значениям. Из таблицы 2 видим, что лучше всего наши данные описывает Экспоненциальная аппроксимация. Заключение В ходе данной работы были аппроксимированы исходные данные с помощью двух программ для работы с массивами данных. Что касается MS Excel, то эта программа, которая основана на работе с таблицами. Она очень удобна для работы с большими массивами данных, при обработке списков и визуализации данных. Так же в ней можно построить графики с учётом аппроксимации данных и линии тренда, выбирая наиболее подходящую аппроксимацию из предложенных MS Excel. В данной работе расчёт производился методом наименьших квадратов, что считалось отдельно вручную, как проверку механизмов MS Excel. Это занимает больше времени, в то время как сама программа работает по принципу наименьших квадратов, так как коэффициенты детерминированности получились одинаковые. Что касается Mathcad, то это программа автоматизации математических расчетов. А также с помощью определенных операторов можно восстанавливать функции регрессии. Нашу задачу мы решали по алгоритму, находя корни определенных систем уравнений вручную. Способ достаточно долгий. Что касается VBA, то эта программа , которая работает на основе Excel. Данная программа удобна для удобного просмотра результатов. Программа работает на основе кода, который пишет сам человек. Нашу задачу мы решали. С помощью последовательного нахождения корней систем с помощью кода. Написание кода и составление визуальной составляющей программы занимает крайне много времени. Но для восприятия результатов эта программа является неоспоримым лидером. Что касается MATLAB, то эта программа, которая позволяет нам увидеть график функции. Данная программа полезна для построения графика посредством написания кода, но не для нахождения значений в табличной форме, что и является главным минусом данной программы. ВыводНайти зависимость между двумя величинами – достаточно распространенная проблема, которую приходится решать во многих сферах жизни. Поэтому современные программы автоматизировали процесс восстановления функции по заданным значениям, что значительно ускоряет этот процесс. Библиографический список Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003—2004. — 311 с. Митин И. В., Русаков В. С. Анализ и обработка экспериментальных данных. — 5-е издание. — 24 с. Очков В. Ф. Mathcad 14 для студентов, инженеров и конструкторов. — СПб.: БХВ-Петербург, 2007. — 368 с. |

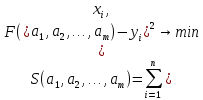
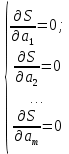
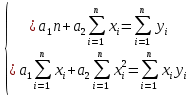
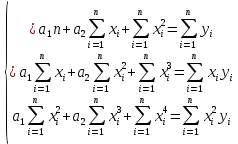
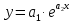
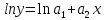
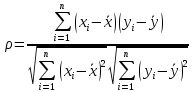 ,
,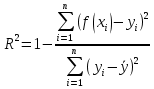 ,
,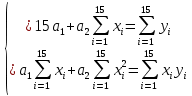
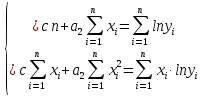 ,
,