задания олимпиада. Зайчихе надо разложить 42 морковки на 7 кучек так, чтобы кучек с одинаковым количеством морковок не было и количество морковок в каждой кучке обозначалось бы однозначным числом. Помогите зайчихе

Название	Зайчихе надо разложить 42 морковки на 7 кучек так, чтобы кучек с одинаковым количеством морковок не было и количество морковок в каждой кучке обозначалось бы однозначным числом. Помогите зайчихе
Дата	12.06.2019
Размер	286.55 Kb.
Формат файла
Имя файла	задания олимпиада.docx
Тип	Документы #81358

5 класс

Зайчихе надо разложить 42 морковки на 7 кучек так, чтобы кучек с одинаковым количеством морковок не было и количество морковок в каждой кучке обозначалось бы однозначным числом. Помогите зайчихе.

3,4,5,6,7,8,9

Расшифруй пример на умножение (каждая буква обозначает одну цифру) и напишите ответы.

Б3 * 1А = А31

А = 7, Б = 4

В XX столетии был такой год, что если его записать цифрами на листе бумаги, а затем этот лист перевернуть вверх ногами – то число на бумаге покажет тот же самый год. Какой это год? Напиши ответ.

1961

С хозяйством попа справляются 10 работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду.

Живет Балда в поповом доме,

Спит себе на соломе,

Ест за четверых,

Работает за семерых.

Поп прогнал лишних работников. Сколько караваев хлеба экономил поп ежедневно?

3

На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?

а) 18 поросят и 12 гусей

b) 13 поросят и 17 гусей

c) 12 поросят и 18 гусей !

d) 12 поросят и 19 гусей

e) 11 поросят и 19 гусей

Винни-Пуху подарили в день рождения бочонок с мёдом массой 7кг. Когда Винни-Пух сьел половину мёда, то бочонок с оставшимся мёдом стал иметь массу 4кг. Сколько килограммов мёда было первоначально в бочонке?

6 кг

6 класс

Можно ли из цифр 1, 2, 3, 4, 5 составить одно двузначное и одно трехзначное число так, чтобы второе делилось на первое?
(Каждая цифра должна быть использована ровно один раз).

Можно. 532 делится на 14, а 215 делится на 43.

В лесу проводился кросс. Обсуждая его итоги, одна белка сказала: «Первое место занял заяц, а второй была лиса». Другая белка возразила: «Заяц занял второе место, а лось был первым». На что филин заметил, что в высказывании каждой белки одна часть верная, а другая – нет. Кто был первым и кто вторым в кроссе?

Запишем кротко высказывания двух белок:

1 – я: «Заяц – I », «Лиса - II ».

2 – я: «Заяц - II», «Лось - I».

Если предположить, что высказывание «Заяц - I» верно, то оба высказывания второй белки будут неверными, а это противоречит условию задачи. Значит высказывание «Заяц – I» не может быть верным, тогда Лиса заняла второе место, а Лось - первое.

Ответ: первым был – Лось, вторым – Лиса.

На день рождения пришло 12 детей в возрасте 6 лет, 7 лет, 8 лет, 9 лет и 10 лет. Четыре ребенка имели возраст 6 лет, а восьмилетних было больше всех. Определите средний возраст 12 детей.
А) 6
Б) 6,5
В) 7
Г) 7,5
Д) 8

Так как число детей младшего возраста равно 4, то число восьмилетних может быть не менее 5. Если их больше 5, то шести и восьмилетних будет больше 9. Тогда на детей возрастов 7 лет, 9 лет и 10 лет останется в сумме только или 1 год или 2 года. Этого быть не может. Значит восьмилетних детей ровно 5 человек. Остаток от 12 составит 3 ребенка. Их надо распределить между возрастами 7 лет, 9 лет и 10 лет. Легко понять, что их ровно по одному человеку.

Получаем следующий расклад:

6 лет — 4 человека
7 лет — 1 человек
8 лет — 5 человека
9 лет — 1 человека
10 лет — 1 человека

Найдем теперь средний возраст — среднее арифметическое имеющихся возрастов. Напомню, что средним арифметическим нескольких чисел называют результат деления их суммы на их количество. Вычисляем его так:

$\dfrac{6\cdot4+7\cdot1+8\cdot5+9\cdot1+10\cdot1}{12}=7,5$

Ответ: 7,5 лет.

Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18.
На какое число делили? A - 18; B - 32; C - 24; D - 36; A - 48;

Решение :

Из условия следует, что 100-4=96 делится на искомое число.
Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число: 96-72=24.
Следовательно, искомое число - 24, так как на него делится и 96, и 72.
Верен ответ (С).

В бутылке, стакане, кувшине и банке находятся «Пепси», «Кока-кола», квас и «Спрайт». Известно, что «Спрайт» и «Пепси» не в бутылке, сосуд с «Кока-колой» находится между кувшином и сосудом с квасом, в банке – не «Кока-кола» и не «Спрайт». Стакан находится около банки и сосуда с «Пепси». Как распределены эти жидкости по сосудам?

Ответ: Квас в банке; «Пепси» в кувшине; «Кока-кола» в бутылке; «Спрайт» в стакане.

7 класс

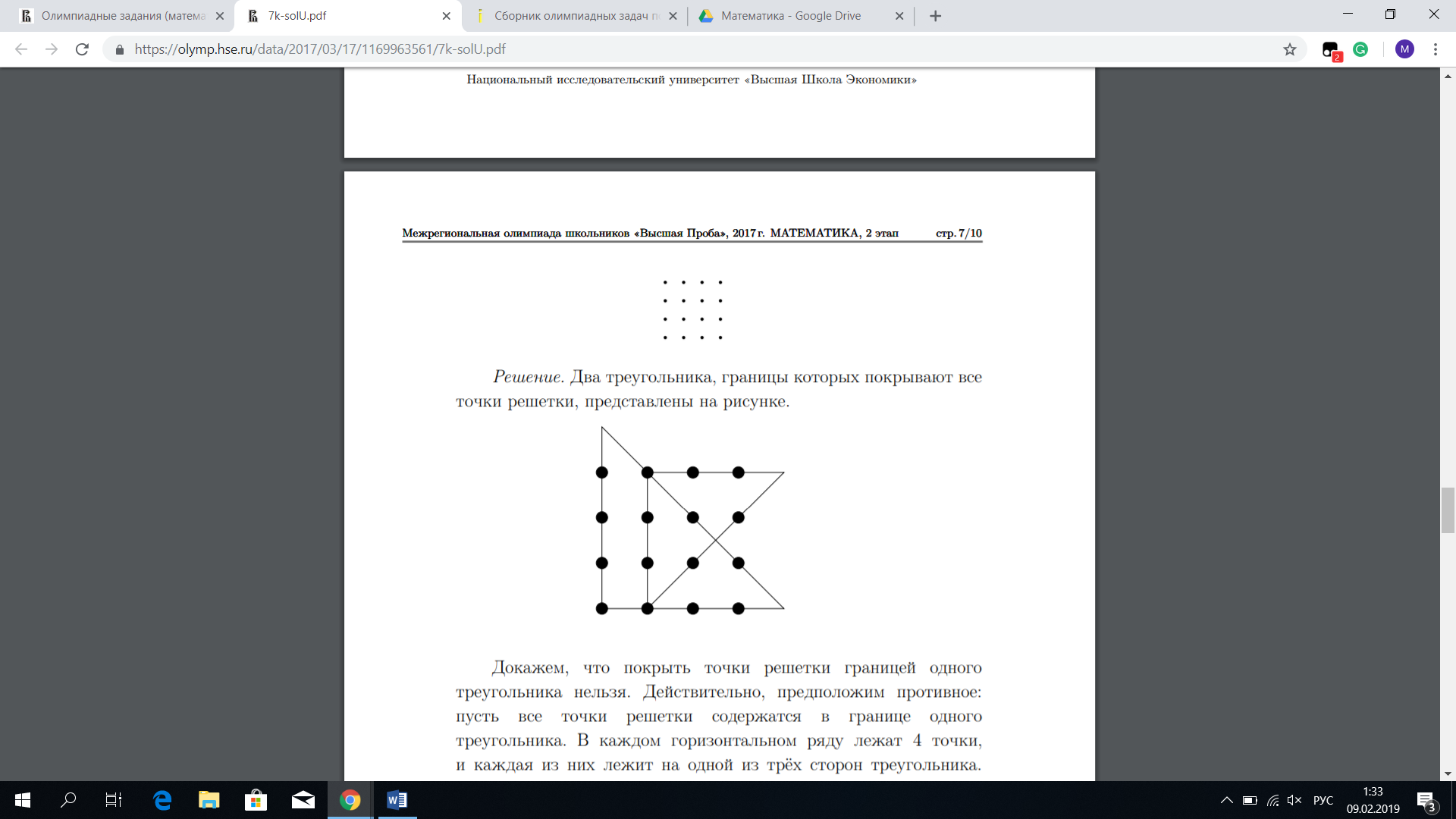
Какое максимальное количество полосок 5×1 можно вырезать из квадрата на клетчатой бумаге размера 8×8 клеток?

Ответ: 12 Решение Заметим, что больше 12 фигурок из 5 клеток в каждой поместить на клетчатую бумагу в которой всего 8×8 = 64 клетки заведомо не удастся (т. к. 64 = 12×5 + 4). Поэтому остается подыскать пример из 12 полосок.

Задача № 2 :

Найти натуральное число A , если из трех следующих утверждений два верны, а одно -- неверно:
а) A + 51 есть точный квадрат,
б) последняя цифра числа A есть единица,
в) A - 38 есть точный квадрат.

Как сказано в условии задачи, одно из этих утверждений является ложным.
В первую очередь на себя обращает внимание условие б).
Если последняя цифра равна 1, то условие а) не верно, так как нет точных квадратов оканчивающихся на 2,
условие в) тоже не может быть верным, так как в этом случае последняя цифра равна 3 и таких точных квадратов нет.
Следовательно, если условие б) верно, то условия а) и в) являются не верными, что не подходит по условию задачи (должно быть два верных и одно неверное утверждение из этих трех).
Следовательно условие б) должно быть ложным, а а) и в) - истинными.

Теперь осталось разобраться с квадратами.
В условиях а) и в) сказано, что A + 51 и A - 38 являются полными квадратами.
Эти квадраты не обязательно могут быть соседними.
Можно легко показать, что если два числа отличаются на число K,
то разность их квадратов делится на это число K тоже.
В нашем случае разность квадратов равна 89 и это число простое,
следовательно эти числа могут отличаться только на 1 или 89.
Последний вариант очевидно не подходит, а проверка первого варианта приводит к ответу A=1974.

Ответ: A = 1974.

В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.

Решение:

Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.
Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах. Значит у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.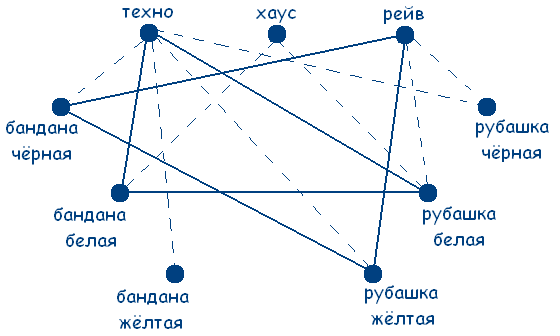

http://logika.vobrazovanie.ru/image/4.png

Ответ:У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.

Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?

Решение:
Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.
Решение лучше и удобнее оформить в виде таблицы:

Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.

Дана квадратная решётка 4 × 4 точек (то есть решётка 3 × 3 с отмеченными 4 × 4 вершинами всех клеток). Какое минимальное число треугольников нужно нарисовать, чтобы каждая точка попала на границу одного из треугольников? Приведите пример с указанным Вами числом треугольников и докажите, почему меньше нельзя. Два треугольника, границы которых покрывают все точки решетки, представлены на рисунке. Докажем, что покрыть точки решетки границей одного треугольника нельзя. Действительно, предположим противное: пусть все точки решетки содержатся в границе одного треугольника. В каждом горизонтальном ряду лежат 4 точки, и каждая из них лежит на одной из трёх сторон треугольника. Следовательно, хотя бы одна сторона содержит две из них, и тем самым, параллельна горизонтальной прямой. Проводя это рассуждение для двух горизонтальных рядов точек решетки получаем, что треугольник имеет две стороны, параллельные горизонтальной прямой, и, тем самым, параллельные друг другу. Полученное противоречие доказывает невозможность покрыть точки решетки границей одного треугольника.