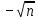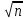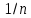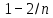Закон больших чисел. Центральная предельная теорема
 Скачать 19.58 Kb. Скачать 19.58 Kb.
|
|
Глава 7. Закон больших чисел. Центральная предельная теорема. § 1. Неравенство Чебышева Пусть случайная величина имеет математическое ожидание М и дисперсию D. Тогда для любого 0 справедливо неравенство Чебышева: 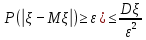 . .Это неравенство часто используют в виде: 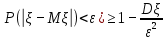 Доказательство этих неравенств основывается на неравенстве Маркова: для любой случайной величины вероятность события не превосходит произведения частного 1 на математическое ожидание модуля случайной величины, то есть Р() 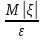 . Справедливо и неравенство Колмогорова: если 1,2,…,n независимые случайные величины имеют конечные дисперсии Di, то для любого 0 справедливо неравенство . Справедливо и неравенство Колмогорова: если 1,2,…,n независимые случайные величины имеют конечные дисперсии Di, то для любого 0 справедливо неравенство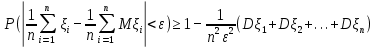 . .Задача 1. В 400 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,8. С помощью неравенства Чебышева оценить вероятность того, что разница междучислом успехов в этих испытаниях и средним числом успехов не превысит 20. Решение. Число успехов в этих испытаниях распределено по закону Бернулли, поэтому среднее число успехов равно М=np=400×0,8=320, а D=npq=400×0,8×0,2=64. Тогда в силу неравенства Чебышева имеем: 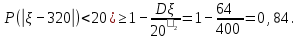 Вычислим эту же вероятность с помощью приближенной (интегральной) формулы Муавра-Лапласа (см. главу 4): 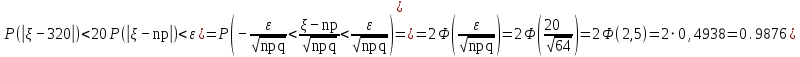 Последнее вычисление показывает, что неравенство Чебышева дает довольно грубые оценки вероятностей. § 2. Закон больших чисел Пусть задана бесконечная последовательность независимых одинаково распределенных случайных величин 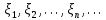 , для которых существуют математическое ожидание , для которых существуют математическое ожидание 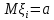 и дисперсия и дисперсия 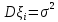 . Тогда для любого >0 . Тогда для любого >0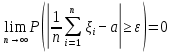 . .Суть закона больших чисел состоит в том, что при возрастании числа слагаемых (т.е. одинаково распределенных случайных величин) среднее арифметическое этих слагаемых мало отличается от математического ожидания 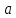 . Любое отклонение среднего арифметического случайных величин от числа . Любое отклонение среднего арифметического случайных величин от числа 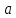 при достаточно большом числе слагаемых – маловероятно. при достаточно большом числе слагаемых – маловероятно. Например. Пусть 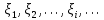 – последовательность случайных величин, каждая из которых равна числу успехов в одном испытании Бернулли (т.е. 1 в случае успеха и 0 – в случае неудачи). Закон распределения каждой такой случайной величины имеет вид: – последовательность случайных величин, каждая из которых равна числу успехов в одном испытании Бернулли (т.е. 1 в случае успеха и 0 – в случае неудачи). Закон распределения каждой такой случайной величины имеет вид:
Здесь 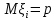 и и 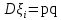 . Тогда среднее арифметическое . Тогда среднее арифметическое 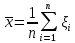 равно частоте успехов в n испытаниях, и закон больших чисел утверждает, что эта частота успехов стремится к вероятности успеха p, если число слагаемых (т.е. число испытаний) стремится к бесконечности. равно частоте успехов в n испытаниях, и закон больших чисел утверждает, что эта частота успехов стремится к вероятности успеха p, если число слагаемых (т.е. число испытаний) стремится к бесконечности. § 3. Центральная предельная теорема (ЦПТ) Если 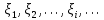 — независимые одинаково распределенные случайные величины, такие, что — независимые одинаково распределенные случайные величины, такие, что 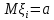 и и 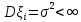 , i = 1, 2, ..., то для любого вещественного х , i = 1, 2, ..., то для любого вещественного х 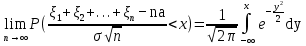 , ,Смысл центральной предельной теоремы заключается в том, что сумма 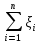 случайных величин при надлежащем «центрировании» и «нормировании» и при увеличении числа слагаемых ( случайных величин при надлежащем «центрировании» и «нормировании» и при увеличении числа слагаемых (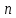 ) ведет себя почти как стандартно распределенная случайная величина. (Напомним, что называется стандартно распределенной, если ) ведет себя почти как стандартно распределенная случайная величина. (Напомним, что называется стандартно распределенной, если 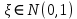 .) .)Например. Пусть 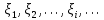 – последовательность случайных величин, удовлетворяющая условиям предыдущего примера. В этом случае сумма – последовательность случайных величин, удовлетворяющая условиям предыдущего примера. В этом случае сумма 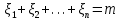 есть число успехов в есть число успехов в 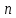 испытаниях Бернулли. Из ЦПТ следует, что испытаниях Бернулли. Из ЦПТ следует, что 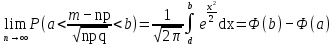 , ,где 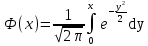 – функция Лапласа. – функция Лапласа.Тогда вероятность того, что число успехов будет заключено между 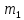 и и 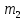 равна равна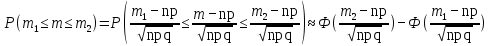 Этот результат называется интегральной теоремой Муавра–Лапласа и используется при npq<9. Если р1 и npq 9 , для биномиального распределения используют пуассоновское приближение 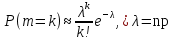 , основанное на формуле Пуассона при р0, n, np. , основанное на формуле Пуассона при р0, n, np.Задача 2. В продукции цеха детали отличного качества составляют 50. Детали укладываются в коробки по 200 шт. в каждой. Какова вероятность того, что число деталей отличного качества в коробке отличаться от 100 не более, чем на 5? Решение. Пусть n - случайное число деталей отличного качества в коробке, тогда при n=200, 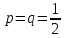 получим: получим: 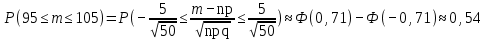 Задача 3. Используя условия предыдущей задачи, указать в каких границах с вероятностью 0,997 находится число деталей отличного качества в коробке. Решение. По таблицам при условии 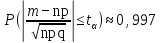 находим t и следовательно, Sn лежит в пределах находим t и следовательно, Sn лежит в пределах 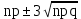 , т.е. число деталей отличного качества в коробке с вероятностью 0,997 находится в пределах 100 21. , т.е. число деталей отличного качества в коробке с вероятностью 0,997 находится в пределах 100 21.Задача 4. Используя условия примера 1, определить, сколько деталей надо положить в коробку, чтобы с вероятностью, не меньшей 0,99, можно было утверждать, что число деталей отличного качества в коробке не меньше 100. Решение. Необходимо найти n из условия Р (Sn 100) 0,99. Используя нормальное приближение, получаем 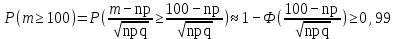 , ,и из таблиц получаем неравенство 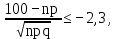 откуда, полагая откуда, полагая 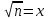 , при , при 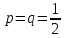 имеем х2-2,3х-2000, откуда получаем n240. имеем х2-2,3х-2000, откуда получаем n240.Задача 5. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей? Решение. Имеем 1000 испытаний Бернулли с вероятностью р=0,005 «успеха», здесь npq5. Применяя пуассоновское приближение с = np = 5, получаем 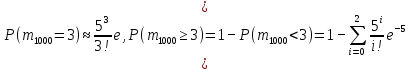 и по таблицам находим: P(m1000 =3) 0,14, Р(m10003) 0,875. Задача 8. Телефонная станция обслуживает 2000 абонентов, в час пик каждый абонент использует связь в среднем в течение 2 минут, т.е. мы считаем, что абонент с вероятностью 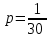 использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ? использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ?Решение. Считая вызовы абонентов независимым, имеем 2000 испытаний Бернулли с вероятностью "успеха" р= 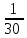 . Надо найти число линий N из условия . Надо найти число линий N из условия Р(m2000N) 0,01. Применяя приближение Пуассона с 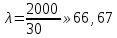 , по таблицам находим N87. При использовании нормального приближения получается, что достаточно 86 линий. , по таблицам находим N87. При использовании нормального приближения получается, что достаточно 86 линий.Задачи для самостоятельного решения Теоретические задачи. Пусть задана последовательность независимых случайных величин 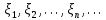 , имеющих следующий закон распределения: , имеющих следующий закон распределения:
Применим ли к этой последовательности закон больших чисел? Пусть задана последовательность независимых случайных величин 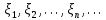 , имеющих следующий закон распределения: , имеющих следующий закон распределения:
Применим ли к этой последовательности закон больших чисел? Доказать закон больших чисел в «обобщенной форме»: пусть 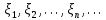 – последовательность случайных величин, у которых существуют математические ожидания – последовательность случайных величин, у которых существуют математические ожидания 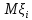 и дисперсии и дисперсии 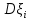 , причем все дисперсии ограничены одной константой C>0. Тогда для любого >0 , причем все дисперсии ограничены одной константой C>0. Тогда для любого >0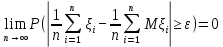 . .Пусть случайная величина имеет нормальное распределение с параметрами М=а, D=2. Найти вероятности 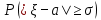 и и 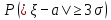 , пользуясь таблицами функции Лапласа, оцените те же вероятности с помощью неравенства Чебышева. , пользуясь таблицами функции Лапласа, оцените те же вероятности с помощью неравенства Чебышева.Пусть случайная величина имеет распределение Лапласа, т.е. ее плотность равна 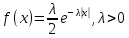 . Найти М и D. Найти вероятности . Найти М и D. Найти вероятности 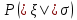 и и 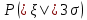 и сравнить их с оценками, получаемыми с помощью неравенства Чебышева. и сравнить их с оценками, получаемыми с помощью неравенства Чебышева.Будет ли выполнен закон больших чисел для последовательности независимых случайных величин 1, 2, ... n , ... если 1). 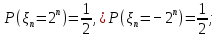 2). Р( 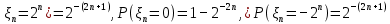 . .Пусть некоторая величина а измеряется прибором без систематической ошибки, но со средним квадратическим отклонением . Это означает, что результат измерения можно считать случайной величиной с М=а, D=2. Какова вероятность при 100 измерениях получить для среднего арифметического (из этих 100 измерений) отклонение от величины а более, чем на 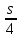 ? Дать оценки этой вероятности с помощью неравенства Чебышева и с помощью ЦПТ. ? Дать оценки этой вероятности с помощью неравенства Чебышева и с помощью ЦПТ.Пусть 1, 2, ... i, ... — независимые, одинаково распределенные случайные величины с функцией распределения F(x). Пусть задана случайная величина 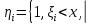 . . Выполняется ли для последовательности 1,2, ... i, ... закон больших чисел? Пусть для последовательностей 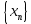 и и 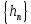 случайных величин существуют числа а и b такие, что случайных величин существуют числа а и b такие, что 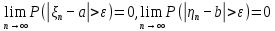 , для любого 0. Доказать, что , для любого 0. Доказать, чтоа) 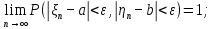 б) если f(x, у) непрерывна в точке (а, b), то для любого 0 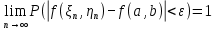 . .Последовательности 1, , ... и 1, 2, ... случайных величин таковы, что 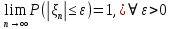 и существует функция распределения F(x), для каждой точки непрерывности которой выполняется соотношения и существует функция распределения F(x), для каждой точки непрерывности которой выполняется соотношения 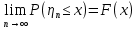 . Доказать, что для каждой точки непрерывности F(x) справедливо равенство . Доказать, что для каждой точки непрерывности F(x) справедливо равенство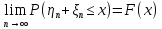 . .Вычислительные задачи. Средний размер вклада в отделении банка равен 6000руб. Оценить вероятность, что случайно взятый вклад не превысит 10000 руб. Среднее количество вызовов, поступающих на АТС завода в течение часа, равно 300. Оценить вероятность того, что в течении следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 300. По статистическим данным в среднем 87% новорожденных доживают до 50 лет. С помощью неравенства Чебышева оценить вероятность того, что из 1000 новорожденных доля доживших до 50 лет будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине). Среднее изменение курса акции компании в течении биржевых торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах курс изменится более, чем на 3%. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено: а) не более 200 клиентов; б) более 150 клиентов. Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. С помощью неравенства Чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74. В среднем 10% работоспособного населения некоторого региона – безработные. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9% до 11% (включительно). Опыт страховой кампании показывает, что страховой случай приходится примерно на каждый пятый договор. Оценить с помощью неравенства Чебышева необходимое количество договоров, которые следует заключить, чтобы с вероятностью 0,9 можно было утверждать, что доля страховых случаев отклонится от 0,1 не более чем на 0,01 (по абсолютной величине). Уточните ответ с помощью следствия из интегральной теоремы Муавра-Лапласа. Дисперсия каждой из 3500 независимых случайных величин равна 5. Оценить вероятность того, что отклонение средней арифметической этих случайных величин от средней математической их математических ожиданий не превысит 0,25. Ежедневно новая сделка заключается с вероятностью 0,2 (но не более одной в день). За сколько дней с вероятностью 0,9 можно ожидать заключения не менее 50 сделок? . В продукции цеха детали отличного качества составляют 80%. В каких пределах будет находиться с вероятностью 0,99 число деталей отличного качества, если взять 10000 деталей. Сделать оценку с помощью неравенства Чебышева и с помощью теоремы Муавра-Лапласа. Театр, вмещающий 1000 человек, имеет два разных входа. Около каждого из входов имеется свой гардероб. Сколько мест должно быть в каждом из гардеробов для того, чтобы среднем в 99 случаях из 100 все эти зрители могли раздеться в гардеробе того входа, через который они вошли? Предполагается, что зрители приходят парами и каждая пара независимо от других выбирает с вероятностью 0,5 любой из входов. На сколько можно будет сократить число мест в гардеробе, если зрители будут приходить поодиночке и также независимо друг от друга с равной вероятностью выбирать любой из входов? Аппаратура состоит из 100 одинаково надежных и независимо работающих элементов, каждый из которых может отказать в течение суток с вероятностью 0,01. На обнаружение отказавшего элемента и его замену требуется 20 минут, в течение которых аппаратура простаивает. а) Найти вероятность того, что время простоя в сутки будет не более 40 минут. б) Найти среднее время простоя аппаратуры в сутки. В поселке 2500 жителей. Каждый из них примерно 6 раз в месяц ездит на поезде в город, выбирая дни поездок по случайным мотивам независимо от остальных. Какой наименьшей вместимостью должен обладать поезд, чтобы он переполнялся в среднем не чаще одного раза в 100 дней (поезд ходит раз в сутки)? На заводе 1000 станков, каждый из которых в среднем в течение 24 дней в месяц потребляет электроэнергию независимо от других станков с некоторой постоянной интенсивностью единиц в день. Какое количество электроэнергии необходимо заводу ежедневно, чтобы не чаще 2 раза в 100 дней он испытывал недостаток электроэнергии? Предприятие выпускает 30% изделий — стоимостью 1 руб., 30% изделий — стоимостью 2 руб. и 40% изделий — стоимостью 3 руб. Какова вероятность получить за 1000 случайно отобранных изделий не менее 2150 руб.? Известно, что 1/3 всех деталей, сходящих с конвейера, подвергается выборочному контролю на основании некоторого случайного признака. Пусть через контроль прошло 100 деталей. В каких пределах с вероятностью 0,99 лежит общее число деталей, сошедших с конвейера? Известно, что вес некоторой детали является случайной величиной , имеющей равномерное распределение на отрезке от 1 до 2г. В каких пределах с вероятностью 0,99 будет находиться суммарный вес 10000 деталей? Для проверки эффективности новый метод стимулирования роста производительности труда был введен на 100 предприятиях. При этом на 32 предприятиях введение нового метода вызвало снижение производительности труда, а на 68 — повышение производительности труда. Какова вероятность того, что чисто случайные колебания вызовут не меньшее отклонение от числа 50 — половины общего числа предприятий?  |