Доклад на тему «Закон больших чисел Чебышева». Закон больших чисел Чебышева
 Скачать 19.51 Kb.
|
|
Михайловский филиал ГАПОУ "Волгоградский медицинский колледж" Доклад на тему: «Закон больших чисел Чебышева» по дисциплине Математика Выполнил: Студент 2 курса группы М-923 Специальности Сестринское дело Кондрашов Михаил Михайловка, 2021 г Введение Итоги отдельных наблюдений, в том числе и проделанных в схожих критериях, имеют все шансы сильно различаться, но в то же время средние итоги для довольно огромного количества наблюдений устойчивы и слабо находятся в зависимости от итогов отдельных наблюдений. Закон больших чисел – это теоретическое объяснение данной характеристики случайных явлений. В это название заключена некоторая группа теорем, которые изъясняют факторы стойкости, а также устанавливают устойчивость средних итогов огромной численности явлений, произошедших случайно. В группу таких теорем входят: 1. Теорема Чебышева; 2. Теорема Бернулли; 3. Теорема Пуассона; 4. Центральная предельная теорема; 5. Теорема Ляпунова. Теорема Чебышева Данная теорема дает такое определение: описывает верхний рубеж вероятности того, что аномалия смысла случайной величины от ее математической надежды больше некого данного количества. Неравенство Чебышева является истоком в основе подтверждения теорем: 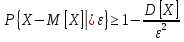 (1)Рассмотрим пример № 81: допустим, что некоторое устройство состоит из 100 элементов, которые работают самостоятельно. Возможность отказа каждого из этих элементов за время т=0,03. Поставить вероятность того, что безусловная величина разницы между математическим ожиданием за время т будет: а) меньше двух; никак не меньше двух. Решение будет состоять в следующем: а) если х станет числом элементов, которые отказали за время т. Тогда м [х] = np = 100 ? 0,03 = 3 и d[x] = npq = 100 ? 0,03 ? 0,97 = 2,91. После того, как мы воспользуемся неравенством Чебышева (подставили в него м[х] = 3, d[х] = 2,91, ɛ= 2), получаем: 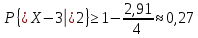 (2)Решение: б) События, которые противоположны |х - 3| < 2 и | х-3| ≥ 2 противоположны, исходя из этого, сумма их вероятностей будет = 1. Получаем: 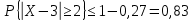 (3)В теореме Чебышева утверждается, что если рассматривается довольно огромное число самостоятельных, независимых величин, которые имеют ограниченные дисперсии, то практически достоверным можно считать явление, суть которого состоит в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно небольшим. При формулировки мной данной теоремы, было предположено, что случайные величины имеют разные математические ожидания. Разумеется, что если опять таки предположить, что дисперсии данных величин урезаны, то к ним станет применима теорема Чебышева. Рассмотрим пример № 83: при каких условиях такой способ, как измерения некой физической величины производят некоторое количество измерений и их среднее арифметическое принимают в качестве искомого размера, можно считать верным? Решение будет состоять в следующем: Ответ на этот вопрос дает теорема Чебышева. Если 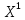 , ,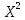  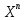... - результаты каждого измерения как случайные величины. К таким величинам можно применять данную теорему только в трех случаях: Ограничены дисперсии (прибор обеспечивает определенную точность измерений); Имеют одинаковое математическое ожидание (измерения проведены без систематических (одного знака) ошибок); Попарно самостоятельны (результат каждого измерения не зависит от результатов остальных). Вывод по теореме Чебышева можно сделать такой: сама теорема указывает условия, при которых такой способ применяется. Но ошибкой станет подумать, что если увеличивая число измерений, можно достичь сколь угодно большой точности. На теореме Чебышева базируется обширно используемый в статистике выборочный способ (генеральная совокупность исследуемых объектов). Закон больших чисел Как было сказано ранее, Закон больших чисел – это теоретическое объяснение данной характеристики случайных явлений. Если случайные величины x 1, x 2, …, x n, … попарно независимы и 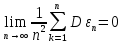 (4)то для любого e > 0 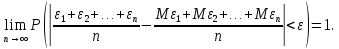 (5)Заключение В ходе работы мною был изучен закон больших чисел, а также были рассмотрена группа теорем, входящих в закон. Под законом больших чисел в теории вероятностей понимается совокупность теорем, в которых устанавливается связь между средним арифметическим достаточно большого числа случайных величин и средним арифметическим их математических ожиданий. Фактическое использование методов теории вероятностей и математической статистики базируется на 2-ух принципах, практически основывающихся на максимальных теоремах: принцип невозможности наступления практически невозможного действия и принцип необходимой убежденности в пришествии действия, возможность которого недалека к 1. В общественно – финансовом значении перед законодательством огромных количеств понимается совместный принцип, в мощь которого количественные закономерности, свойственные глобальным публичным явлениям, четко появляются только в довольно великом количестве надзоров. Закон больших чисел порожден особенными качествами глобальных социальных явлений. Последние, в силу своей собственной особенности, имеют отличия друг от друга, но и имеют что то общее, обусловленное их приспособлением к конкретному виду, классу, к конкретным группам. Тенденции и закономерности, вскрытые с помощью закона больших чисел, - это массовые статистические закономерности.
1. Колмогоров A.H. Теория вероятностей и математическая статистика. — М.: Наука, 1986.; 2. http://www.dissercat.com/content/zakon-bolshikh-chisel-dlya-otritsatelno-assotsiirovannykh-sluchainykh-velichin; 3. Прохоров Ю.В. Одна экстремальная задача теории вероятностей // Теория вероятностей и ее применения. — 1959.; 4. http://cito-web.yspu.org/link1/metod/theory/node21.html; 5. http://www.exponenta.ru/educat/class/courses/tv/theme0/6.asp; 6. http://www.grandars.ru/student/vysshaya-matematika/formula-puassona.html. |