физическая химия. физхим. Закон действия масс Закон действующих масс
 Скачать 62.11 Kb.
|
|
Закон действия масс Закон действующих масс устанавливает соотношение между массами реагирующих веществ в химических реакциях при равновесии, а также зависимость скорости химической реакции от концентрации исходных веществ. Закон действующих масс открыли в 1864—1867 годах норвежские ученые К.Гульдберг (1836—1902) и П.Вааге (1833—1900). Закон действующих масс справедлив только для газов и жидких веществ (гомогенных систем) и не выполняется для реакций с участием твёрдых веществ (гетерогенных систем). В 1865 г. профессор Н.Н. Бекетов впервые высказал гипотезу о количественной взаимосвязи между массами реагентов и временем течения реакции: "...притяжение пропорционально произведению действующих масс". Эта гипотеза нашла подтверждение в законе действующих масс, который был установлен в 1867 г. двуми норвежскими химиками К. Гульдбергом и П. Вааге. Современная формулировка закона действующих масс такова: При постоянной температуре скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных стехиометрическим коэффициентам в уравнении реакции. Для реакции aA + bB → mM + nN математическое выражение закона действующих масс имеет вид: v = k · CAa · CBb, где v - скорость реакции; k - коэффициент пропорциональности, называемый константой скорости химической реакции (при CA = CB = 1 моль/л k численно равна v); CA и CB - концентрации реагентов A и B; a и b - стехиометрические коэффициенты в уравнении реакции. Константа скорости химической реакции k определяется природой реагирующих веществ и зависит от температуры, от присутствия катализатора, но не зависит от концентрации веществ, участвующих в реакции. Закон действующих масс справедлив только для наиболее простых по своему механизму взаимодействий, протекающих в газах или в разбавленных растворах. Часто уравнение реакции не отражает ее механизма. Сложные реакции могут быть совокупностью параллельно или последовательно протекающих процессов. Закон действующих масс справедлив для каждой отдельной стадии реакции, но не для всего взаимодействия в целом. Та стадия скорость которой минимальна, лимитирует скорость реакции в общем. Поэтому математическое выражение закона действующих масс, записанное для самой медленной (лимитирующей) стадии процесса, приложимо одновременно ко всей реакции в целом. Формы констант равновесия и соотношения между ними 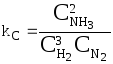 - константа равновесия, выраженная через молярные концентрации веществ, участвующих в химической реакции.Кроме того константу равновесия можно выразить через парциальные давления реагирующих веществ:  .Константу равновесия можно выразить через числа молей веществ - участников реакции: 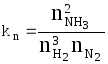 .Константу равновесия можно выразить и через мольные доли участников реакции: 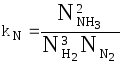 .В общем случае kC 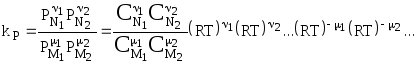 kP kn kN, но между ними существует связь. Для ее установления целесообразно обратиться к химической реакции, записанной в общем виде: . (1.1) .Откуда  , (1.2)где  - изменение количества вещества в результате химической реакции.Для идеальных газов их парциальные давления связаны с общим давлением соотношением:  ,поэтому:  или  . (1.3)Дал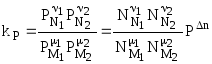ее:  или окончательно:  . (1.4)Зависимость скорости и константы скорости химической реакции от температуры. Влияние температуры на скорость химических реакций Из качественных соображений понятно, что скорость реакций должна увеличиваться с ростом температуры, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения - правило Вант-Гоффа и уравнение Аррениуса. Правило Вант-Гоффа заключается в том, что при нагревании на 10оС скорость большинства химических реакций увеличивается в 2  4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом: , (1.5)где  - температурный коэффициент скорости ( = 2 4). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости:  , (1.6)где R - универсальная газовая постоянная; A - предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом реакции; EA - энергия активации, которую можно охарактеризовать как некоторую пороговую энергию: грубо говоря, если энергия сталкивающихся частиц меньше EA, то при столкновении реакция не произойдет, если энергия превышает EA, реакция произойдет. Энергия активации не зависит от температуры. Графически зависимость k(T) выглядит следующим образом:  При низких температурах химические реакции почти не протекают: k(T)  0. При очень высоких температурах константа скорости стремится к предельному значению: k(T) A. Это соответствует тому, что все молекулы являются химически активными и каждое столкновение приводит к реакции.Энергию активации можно определить, измерив константу скорости при двух температурах. Из уравнения (1.6) следует:  . (1.7)Более точно энергию активации определяют по значениям константы скорости при нескольких температурах. Для этого уравнение Аррениуса (1.6) записывают в логарифмической форме  и записывают экспериментальные данные в координатах ln k - 1/T. Тангенс угла наклона полученной прямой равен -EA / R. Для некоторых реакций предэкспоненциальный множитель слабо зависит от температуры. В этом случае определяют так называемую опытную энергию активации:  . (1.8)Если предэкспоненциальный множитель - постоянный, то опытная энергия активации равна аррениусовской энергии активации: Eоп = EA. |