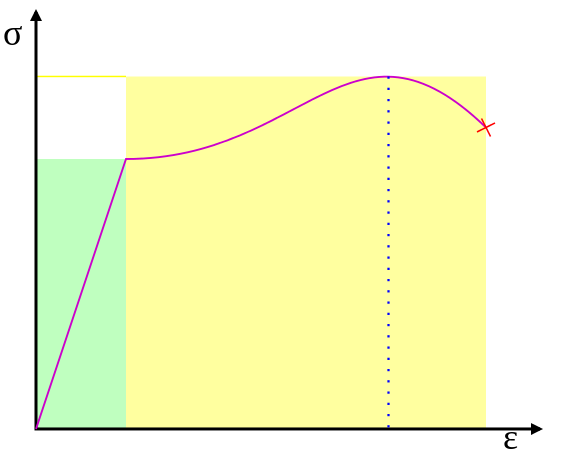
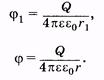экз физика. Закон Гука. Модуль Юнга

• Название: Закон Гука. Модуль Юнга
• Дата: 23.12.2021
• Размер: 207.12 Kb.
• Имя файла: экз физика.docx
• Тип: Закон; #314813

Механическое напряжение. Закон Гука. Модуль Юнга.

Механическое напряжение — это векторная физическая величина, мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов.



Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.

Для тонкого растяжимого стержня закон Гука имеет вид:



Коэффициент упругости (размерность L⁰MT^-2) зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины   ) явно, записав коэффициент упругости как



Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.

Модуль Юнга рассчитывается следующим образом:



Если ввести относительное удлинение



и нормальное напряжение в поперечном сечении



то закон Гука для относительных величин запишется как



В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

текучесть

Область пропор- циональности

предел упругости

32 Внутренняя энергия реального и идеального газа. Способы измерения внутренней энергии. Работа в термодинамике. Геометрическое истолкование работы. Количество теплоты. Удельная теплоемкость вещества.

ермодинамика

 – это теория тепловых явлений, происходящих в макротелах и их системах без учета атомно-молекулярного строения тела.

Термодинамика изучает свойства термодинамической системы в состоянии термодинамического равновесия и процессы перехода этих систем из одного состояния в другое.

В теплоизолированном цилиндре под невесомым поршнем находится идеальный газ. Сообщим системе некоторое количество теплоты Q и воздействуем на поршень некоторой внешней силой F. Рассмотрим, как изменяются параметры системы

Состояние термодинамической системы характеризуется рядом физических величин, главной из которых является внутренняя энергия.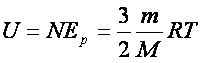



Существует два способа изменения внутренней энергии тела:

1. Теплопередача – это процесс передачи энергии от одного тела к другому без совершения работы. Виды теплопередачи:

В теплоизолированном цилиндре под невесомым поршнем находится идеальный газ. Сообщим системе некоторое количество теплоты Q и воздействуем на поршень некоторой внешней силой F. Рассмотрим, как изменяются параметры системы

Состояние термодинамической системы характеризуется рядом физических величин, главной из которых является внутренняя энергия.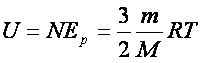



Существует два способа изменения внутренней энергии тела:

1. Теплопередача – это процесс передачи энергии от одного тела к другому без совершения работы. Виды теплопередачи: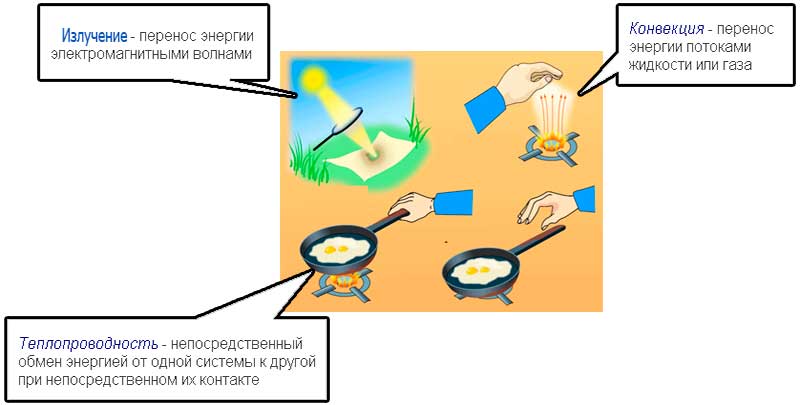



Количество теплоты, переданное при нагревании тела или выделяемое при его охлаждении:

Q=cmΔT

c – удельная теплоемкость вещества

Количество теплоты, идущее на плавление тела или выделяемое при его кристаллизации:

Q=λm

λ – удельная теплота плавления и кристаллизации тела

Количество теплоты, идущее на испарение жидкости при T=const или выделяемое при конденсации пара:

Q=Lm

L – удельная теплота парообразования и конденсации

В координатах p, V работа газа равна площади фигуры под графиком зависимости давления от объема.

Изменение внутренней энергии тела (системы тел) определяется первым законом (началом) термодинамики

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе: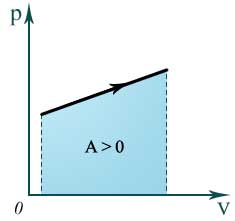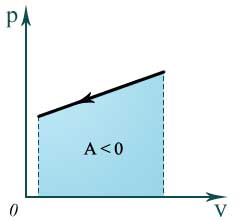

                    

Если система сама совершает работу над внешними силами, то А=-А‘ и первый закон термодинамики запишется так:



Изопроцессы в термодинамике

Простейшими процессами перехода термодинамической системы из одного состояния в другое являются:

Изобарный процесс p=const

Q=ΔU+A’

Изохорный процесс V=const

Q=ΔU

Газ не меняет своего объема, работа им не совершается. Т.о переданное количество теплоты идет на увеличение внутренней энергии газа.

Изотермический процесс T=const

Q=A’

Внутренняя энергия не меняется. Следовательно количество теплоты, переданное системе идет на совершение работы

Адиабатный процесс Q=0

A=ΔU

Процесс происходящий в системе без теплообмена с окружающей средой. При совершении работы над газом внутренняя энергия системы увеличивается, следовательно увеличивается и температура газ

33 Элементарный заряд. Электризация тел. Закон сохранения заряда. Закон Ку­лона.

Электризация - процесс получения электрически заряженных тел из электронейтральных.

Любое тело является заряженным если оно содержит положительный и отрицательный заряд в неравных количествах.

Заряд - это физическая величина, характеризующая степень электромагнитного взаимодействия.

Единица электрического заряда в системе СИ- Кулон (Кл)

Заряд можно разделить до наименьшего значения.

Элементарный электрический заряд равен 1,6×10-19 Кл и существует в двух видах: элементарный положительный заряд и элементарный отрицательный заряд.

Носителем элементарного положительного электрического заряда является протон. mp = 1,67×10-27 кг.

Носителем элементарного отрицательного электрического заряда является электрон. me = 9,11×10-31 кг.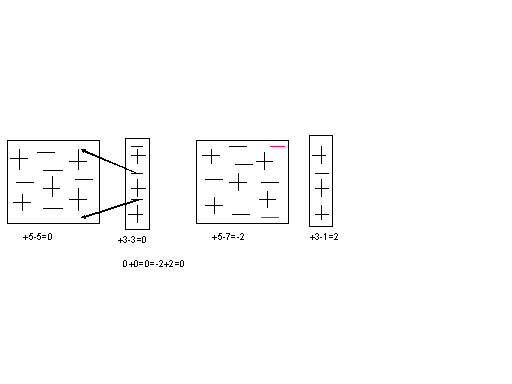

 Электризация трением

Электризация через влияние



Электризация соприкосновением с заряженным телом



Закон сохранения электрического заряда

алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной, какие бы процессы в этой системе не происходили.

q1+ q2 + …+ qi = const.

где q1, q2, ... qi - заряды

Замкнутой называют систему, не обменивающуюся зарядами с внешними телами.

Закон Кулона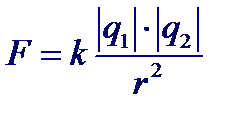

 Силы взаимодействия точечных неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ним

34 Электростатическое поле и его свойства. Напряженность и потенциал поля. Разность потенциалов. Силовые линии электростатического поля. Формула связи напряженности и разности потенциалов. Эквипотенциальные поверхности.

Электрическое поле есть разновидность материи, посредством которой осуществляется силовое воздействие на электрические заряды, находящиеся в этом поле Характе­ристики электрического поля, которое генерируется биологическими структурами, являются источником информации о состоянии организма

Силовой характеристикой электрического поля является напряженность, равная отношению силы, действующей в данной точке поля на точечный заряд, к этому заряду

 (12.1)

Напряженность — вектор, направление которого совпадает с направлением силы, действующей в данной точке поля на положительный точечный заряд.

Напряженность электрического поля в произвольных точках аналитически задается следующими тремя уравнениями:

Е_х = f₁(x, у, z); Е_у = f₂(х, у, z); E_z = f₃(x, у, z), (12.2)

где Е_х, Е_у и E_z — проекции вектора напряженности на соответствующие координатные оси, введенные для описания поля. Электрическое поле графически удобно представлять силовыми линиями,касательные к которым совпадают с направлением вектора напряженности в соответствующих точках поля.

Обычно эти линии проводят с такой густотой, чтобы число линий, проходящих сквозь единичную площадку, перпендикулярную им, было пропорционально значению напряженности электрического поля в месте расположения площадки.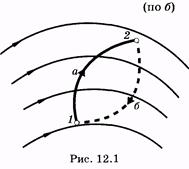

Представим себе, что заряд q перемещается в электрическом поле по траектории 1-а-2 (рис. 12.1). Силы поля при этом совершают работу, которую можно выразить через напряженность [см. (12.1)]:

 (12.3)

где dl — элементарное перемещение; E_l — проекция вектора  на направление  . Покажем, что работа сил электростатического поля (электрического поля неподвижных зарядов) не зависит от траектории, по которой перемещается заряд в этом поле. Поля, обладающие таким свойством, называют потенциальными.

Пусть заряд q переместился по замкнутой траектории 1-а-2-б-1 (рис. 12.1). Так как поле электростатическое, то положение зарядов, создающих поле, при этом не изменилось, и потенциальная энергия, зависящая от их взаимного положения, осталась прежней. Поэтому работа сил электростатического поля по переме­щению заряда по замкнутой траектории равна нулю: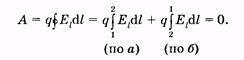



(12.4)

Так как силы, действующие на заряд q, определяются его положением в поле, то выражения для работ сил поля при перемещении заряда по одной и той же траектории в противоположных направлениях отличаются только знаком:



(по б) (по б)

Подстановка этого выраже­ния в (12.4)дает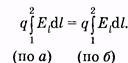



(12.5)

Равенство (12.5) означает, что работа сил электростатического поля не зависит от траектории заряда, а зависит от величины заряда, положения начальной и конечной точек траектории и от напряженности поля.

На основании этого свойства вводят понятие разности потенциалов Dj, которая для электростатического поля равна напряжению U.

Разностью потенциалов между точками поля называют отношение работы, совершаемой силами поля при перемеще­нии точечного положительного заряда из одной точки поля в другую, к этому заряду: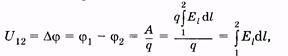

 (12.6)

где j₁ и j₂ — потенциалы в точках 1 и 2 электрического поля, U₁₂— напряжение между этими точками. Разность потенциалов между двумя точками зависит от положения выбранных точек и от на­пряженности электрического поля, как следует из (12.6).

Наряду с разностью потенциалов в качестве характеристики электрического поля используют понятие потенциала. Однако для данной точки поля оно имеет однозначный смысл только в том случае, если задан потенциал какой-либо произвольной точки поля. На практике принято считать, что потенциал проводников, соединенных с землей, или потенциал шасси, на котором смонти­ровано радиоустройство (и в том и в другом случаях говорят о за­землении), равны нулю. В теоретических задачах обычно считают равным нулю потенциал бесконечно удаленных точек.

Вычислим потенциал поля точечного заряда,расположенного в однородном изотропном диэлектрике с диэлектрической проницаемостью e (рис. 12.2). Пусть точки 1 и 2 находятся на одной силовой линии ни расстояниях соответственно r₁ и r₂ от источника поля — заряда Q. Проинтегрируем выражение (12.6) по отрезку 1—2, учитывая, что в соответствии с законом Кулона (для точечного заряда) Е_l = E = Q/(4pe e₀r²) и dr = dl: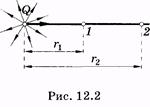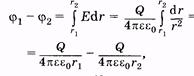

   (12.7)

где e₀ » 8,85 • 10 ¹² Ф/м — электрическая постоянная¹.

(¹ Размерность электрической постоянной e₀ выражается также в виде  , что следует из закона Кулона).

Предположим, что потенциал в бесконечно удаленной точке равен нулю: j₂ ®0 при r₂ ® ¥. Тогда из (12.7) получаем

или в более общем виде (12.8)

Могли быть и другие предположения относительно значения потенциала в бесконечно удаленной точке, однако сделанное выше допущение привело к наиболее простому выражению (12.8), по которому обычно и вычисляют потенциал поля точечного заряда.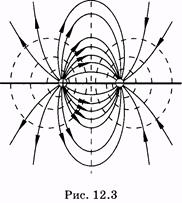

Потенциалы электрического поля в различных точках наглядно можно представить в виде поверхностей одинакового потенциала (эквипотенциальных поверхностей). Обычно проводят экви­потенциальные поверхности, отличающиеся от соседних на одно и то же значение потенциала. На рис. 12.3 изображены эквипотенциальные поверхности (штриховые линии) и силовые линии (сплошные) поля двух разноименных одинаковых точечных зарядов.

Аналитически зависимость электрического потенциала от координат в разных точках поля задается некоторой функцией координат

j = f(x, у, г),(12.9)

которая в частных случаях может иметь, например, вид (12.8). Так как напряженность электрического поля определяется через силу, а потенциал — через работу сил поля, то эти характеристики связаны между собой аналогично силе и работе. Интегральная зависимость напряженности поля и потенциала дается формулой (12.6) или выражением

 (12.10)

Здесь с учетом знака «-» изменены пределы интегрирования: верхнему пределу интеграла соответствует в левой части уменьшаемое j₂, нижнему — вычитаемое j₁.

Получим дифференциальную связь между Е и j_. Предположим, что точки 2 и 1 расположены сколь угодно близко, тогда из (12.10) получим

(12.11)

Производная от потенциала по направлению dj/dl характеризует отношение приращения потенциала dj к соответствующему расстоянию dl в некотором направлении l; Е_l— проекция вектора 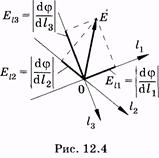 на это направление.

Смысл формулы (12.11) виден из рис. 12.4. В точке 0 проведен вектор  , который спроецирован на направления l₁, l₂ и l₃. Эти проекции по модулю равны производным от потенциала по соответствующим направлениям: çdj/dl₁ç, çdj/dl₂ç, çdj/dl₃ç.Наиболь­шее изменение потенциала, приходящееся на единицу длины, происходит вдоль прямой, совпадающей с  ; знак «минус» в (12.11) означает, что потенциал быстрее всего убывает в направлении  и быстрее всего возрастает в направлении - Е. Можно сказать, что вектор  равен взятому с обратным знаком градиенту потенциала:

(12.12)

В направлении, перпендикулярном силовой линии, имеем

(12.13)

Из этого следует, что силовые линии и эквипотенциальные поверхности взаимно перпендикулярны.Если поле однородно, например поле плоского конденсатора, то из формулы (12.6) находим что для двух точек, расположенных на одной силовой линии на расстоянии l,

 (12.14)

Учитывая (12.11) и (12.9), можно записать проекции вектора напряженности электрического поля по трем координатным осям:



 (12.15)

Тогда напряженность определяют по формуле

 (12.16)

Если поле создано N точечными зарядами, то напряженность в некоторой точке можно вычислить как векторную сумму напряженностей полей, создаваемых в этой точке каждым зарядом отдельно (принцип суперпозиции):

 (12.17)

а электрический потенциал в этой точке — как алгебраическую сумму потенциалов от каждого заряда, предполагая, что потенциал бесконечно удаленных точек равен нулю:

 (12.18)

Существующие электроизмерительные приборы рассчитаны на измерение разности потенциалов, а не напряженности. Ее можно найти из этих измерений, используя связь  и j.