ГМП1. Закон изучающий движение жидкостей гидродинамика идеальные жидкости абсолютно несжимаема под действием p
 Скачать 20.97 Kb. Скачать 20.97 Kb.
|
|
ГМП-1 Классификация жидкостей. Физические свойства капельных жидкостей. Дифференциальные уравнения равновесия Эйлера Закон изучающий движение жидкостей – ГИДРОДИНАМИКА Идеальные жидкости - абсолютно несжимаема под действием p - не изменяется плотность при изменение температуры - не обладает вязкостью РЕАЛЬНЫЕ ЖИДКОСТИ КАПЕЛЬНЫЕ - практически несжимаемы и обладают очень малым коэффициентом объемного расширения УПРУГИЕ - V сильно изменяется при изменение t и p Физические св-ва жидкостей Плотность и удельный вес Плотность(ρ) =m/V Удельный вес (γ) γ =G/V СИ -н/м^3 Масса и вес связаны мд собой соотношением m =G/g γ = ρg Плотность газов мб рассчитан уравнением pV=(m/M)RT Давление p =γH = ρgH избыточное давление=абсолютное давление- атмосферное давление разрежение давления =атмосферное -абсолютное Вязкость Свойство жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц, называют ВЯЗКОСТЮ. 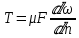 Где T- касательная сила , F- поверхность соприкосновения слоев , 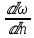 – градиент скорости – градиент скорости 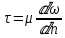 Тк таун всегда положительна , то правая часть уравнения зависит от градиента . из за уменьшения скорости градиент остается отрицательным . 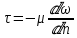 Дифференциальные уравнения равновесия Эйлера В объеме жидкости, находящейся в покое, выделим параллелепипед объемом dV c ребрами dx, dy и dz. Сила тяжести, действующая на паралл. Равна произведению его массы на ускорение свободного падения. Сила гидростатического давления равна произведению гидростатического давления на площадь грани . Т.к. жидкость находиться в состоянии покоя, то другие силы равны 0. Рассмотрим ось z: 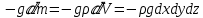 Сила гидростатического давления по оси z действует на на нижний и на верхний грань 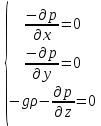 2. Основное уравнение гидростатики. Некоторые практические приложения основного уравнения гидростатики. Из уравнения покоящийся жидкости изменяется только по вертикали , а давление вдоль осей x и y равны 0. Т.к. уравнения по осям x и y равны 0, то частная производная z может быть записана в виде 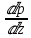 Отсюда следует что 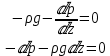 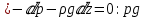 Разделив на плотность и ускорение свободного падения мы получаем 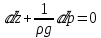 для несжимаемой однородной жидкости плотность постоянна и, следовательно 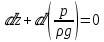 далее интегрируем и получаем 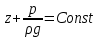 Z – нивелирная высота. Эта уравнение является основным уравнением гидростатики. Некоторые практические приложения основного уравнения гидростатики. Рассмотри 3 практич. приложения Принцип сообщающихся сосудов и его использование Пусть 2 открытых сообщающихся сосуда заполнены жидкостью плотностью p. Выберем произвольно плоскость сравнения 0-0и некоторую точку А внутри жидкости. Если считать т. А принадлежащей левому сосуда то 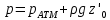 Если правому сосуда то 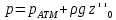 При равновесии для каждой точки давление одинаково в любом направлении Тогда 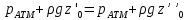 Отсюда следует, что z”=z’ Пневматическое измерение количества жидкости в резервуарах Для контроля давления в каком либо резервуаре (например в подземном) внего помещают трубу. Давление над жидкостью равна p0. По трубе подают сжатый газ или каой либо газ постепенно повышая давление , когда воздух преодолеет сопротивление столба жидкости и начнет барботировать давление перестанет возрастать и будет ровно согласно уравнению 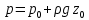 А уровень жидкости выводиться из этого уравнения Объем можно найти по z0 и по поперечному сечению Идр Гидродинамика. Скорость и расход жидкости. Установившийся и неустановившийся потоки. Уравнение неразрывности (сплошности) потока. Гидродинамика Закон ГИДРОДИНАМИКИ позволяет находить разность давлений , необходимую для перемещения данного количества жидкости с требуемой скоростью и расход энергии на перемещение или наоборот. Различаю Внутреннюю Связана с анализом движения жидкостей внутри труб Внешнюю Изучение закономерностей отекания жидкостями различных тел Смешанную Анализ движения при зернистых покрытиях внутри труб Скорость и расход жидкости Количество жидкости, протекающий чз поперечное сечение потока в единицу времени, называют РАСХОДОМ ЖИДКОСТИ Объемный расход Средняя скорость к площади живого сечения потока Q=wS (м^3/с) Массовый расход Произведения плотности жидкости на объемный расход M=pQ(кг/с) Средняя скорость w =Q/S Массовая скорость W=pw Плотность на среднюю скорость |
