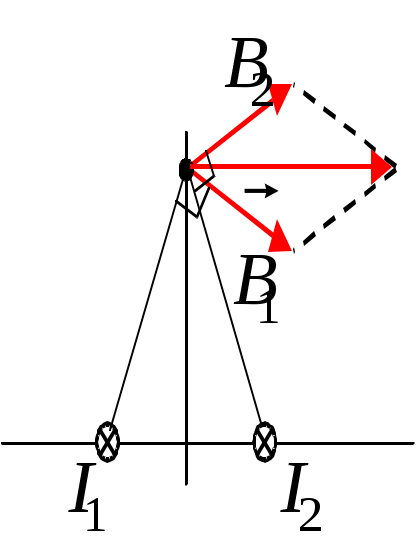
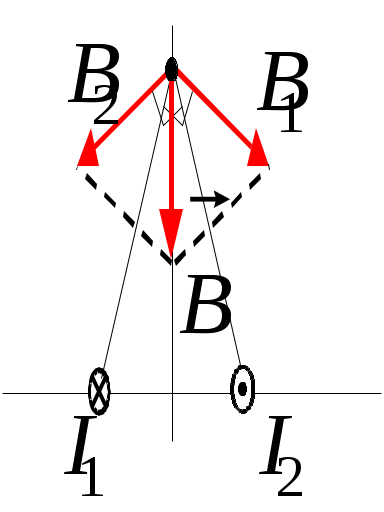
Аа. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции
 Скачать 2.07 Mb.
|
ОтветыОтвет «Б». Точечный заряд q создает в точке A поле напряженностью  , г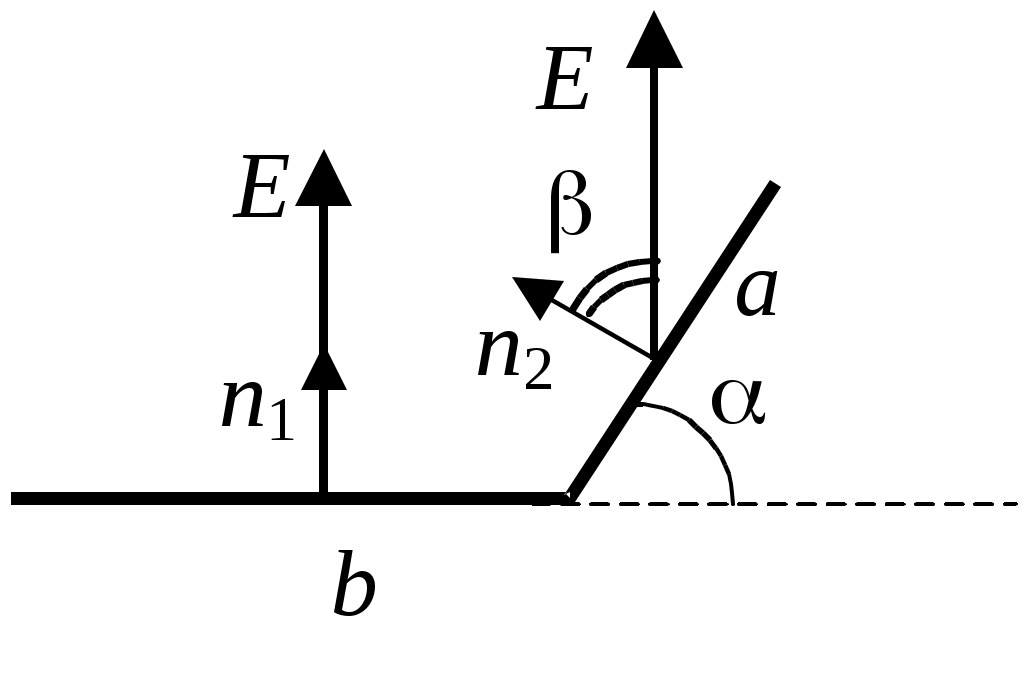де  - вектор, проведенный от заряда q в точку A. В данном случае  . И  зобразим рисунок «в разрезе». Выбрав направление нормали, как показано на рисунке, и воспользовавшись определением потока вектора, запишем: .Учитывая, что  , найдем  .По теореме Гаусса поток вектора напряженности через замкнутую поверхность равен  , где  - заряд, который попадает внутрь замкнутой поверхности. В данном случае равен заряду круга радиуса R, который «вырезает» цилиндр в плоском листе. Так как лист заряжен однородно, то  . Следовательно,  .Воспользуемся теоремой Гаусса. Выберем замкнутую поверхность в виде сферы радиуса 2R, центр которой совпадает с общим центром заряженных сфер. Тогда  .Учитывая, что  , получим .Ответ «В». В пунктах А), Б) и Г) приведены математически эквивалентные формулы, выражающие теорему Гаусса в дифференциальном виде Ответ «В». Разность потенциалов точек 1 и 2 однородного электростатического поля определяется формулой  ,где вектор  проведен из точки 1 в точку 2, - угол между векторами и  . Учитывая, что  , получаем ответ. По определению разность потенциалов в точках 1 и 2 равна:  ,где интегрирование проводится по произвольной кривой, соединяющей точки 1 и 2. В данном случае эти точки лежат на оси x и интегрировать будем вдоль этой оси: 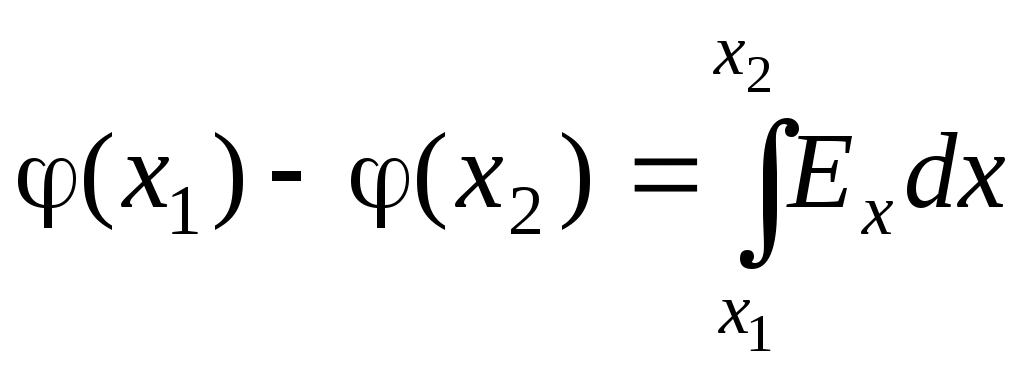 .Численной значение этого интеграла определим, вычислив площадь под графиком зависимости  :  2 В.Если однородно заряженная плоскость перпендикулярна оси X и расположена при  , то ее электрическое поле можно выразить формулами при  ;  при  .Нетрудно убедится, что эти формулы справедливы при любом знаке поверхностной плотности заряда . Принимая координаты начальной и конечной точек равными  и  , получим .Из формулы  найдем проекции вектора напряженности: ,  .Модуль вектора напряженности равен  .Ответ «А». Воспользуемся формулой  .Поскольку сторона кубика достаточно мала, то каждую частную производную можно заменить отношением приращения функции (потенциала) к приращению соответствующего аргумента (координаты). При этом остальные аргументы, по которым не проводится дифференцирование, должны оставаться постоянными. Например 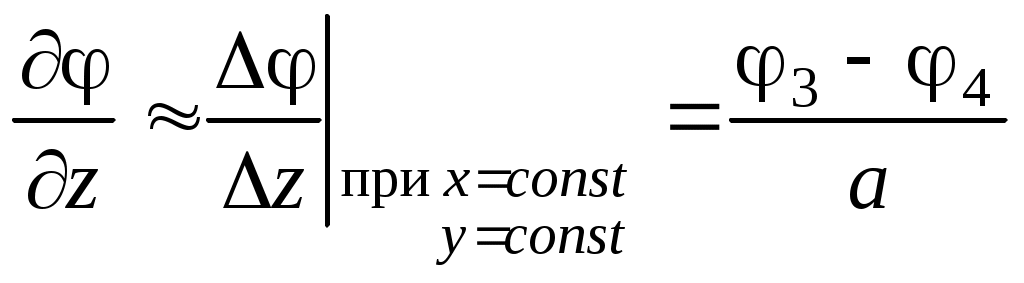 .При перемещении точечного заряда q из точки с потенциалом  в точку с потенциалом  электрическое поле совершает работу .Примем, как обычно, потенциал в бесконечно удаленной точке равным нулю:  . Потенциал в начале координат найдем, воспользовавшись принципом суперпозиции: .Окончательно получим  .Ответ «Б», «В». Известно, что потенциал электростатического поля определен с точностью до произвольной аддитивной постоянной. Переписывая формулу В) в виде  ,замечаем, что она отличается от формулы Б) на постоянную  . Ясно, что напряженность поля в случаях Б) и В) будет одинакова.Ответ «А». Потенциал вне однородно заряженной сферы на расстоянии r от ее центра равен  ,а внутри сферы потенциал такой же, как на ее поверхности:  .Поэтому разность потенциалов в точках 1 и 2 равна  .З 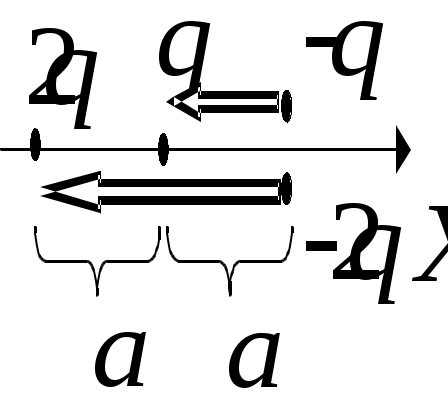 аряд (–3q) представим в виде двух зарядов (–q) и (–2q). Из рисунка видно, что заданную систему зарядов можно представить в виде системы двух диполей с одинаково направленными дипольными моментами. Модуль дипольного момента системы равен .Ответ «А». Потенциал поля точечного диполя определяется формулой  ,г 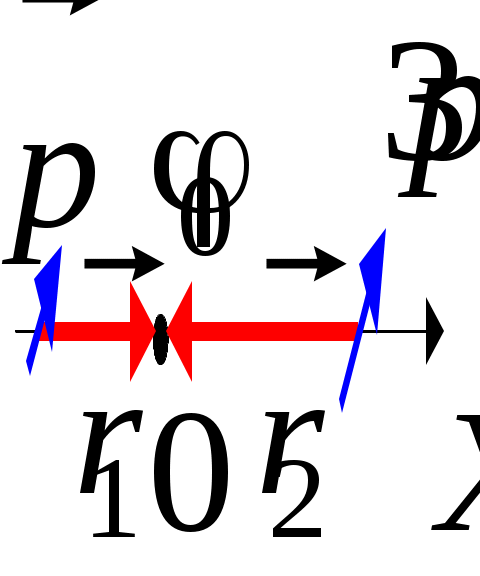 де  - вектор, проведенный от диполя в точку, в которой рассчитывается потенциал. Потенциал в начале координат равен .Учитывая, что  ,  ,  (см. рис.), получим .Учитывая, что проекция вектора  на ось X положительна, получаем  .Вектор момента сил, действующих на диполь со стороны внешнего электрического поля , равен   , а его величина  , где -угол между векторами и . Для отношения величин моментов получим: .Потенциал в точек, положение которой определяется вектором , проведенным от диполя в эту точку, определяется формулой . Из этой формулы следует, что  .Ответ «А». Внутри проводника напряженность поля равна нулю, а заряд располагается только на его поверхности. Поэтому:  ,где  - поверхностная плотность заряда i-ой площадки,  - ее площадь,  -вектор, проведенный от этой площадки в точку наблюдения (где вычисляется поле ). При увеличении суммарного заряда проводника в 2 раза напряженность поля внутри проводника должна остаться равной нулю. Это возможно в том случае, если поверхностная плотность заряда каждой малой площадке увеличится в 2 раза. Такое распределение заряда является единственно возможным (в силу теоремы единственности решения задачи электростатики).Ошибочное утверждение «Б». Напряженность электростатического поля внутри проводника равна нулю. Поэтому разность потенциалов в двух произвольных точках проводника равна нулю и, следовательно, потенциал всех точек проводника имеет одинаковое значение (не обязательно равное нулю). Ответ «Б». Выберем замкнутую поверхность, целиком расположенную в шаре и охватывающую полость. Вектор напряженности электрического поля во всех точках этой поверхности равен нулю. Поэтому и поток вектора напряженности через эту поверхность равен нулю. Из теоремы Гаусса следует, что Q1 = 0. При этом Q2 = 2q. Ответ «Б». Выберем замкнутую поверхность, целиком расположенную в проводнике и охватывающую полость. Вектор напряженности электрического поля во всех точках этой поверхности равен нулю. Поэтому и поток вектора напряженности через эту поверхность равен нулю. Из теоремы Гаусса следует, что суммарный заряд внутри поверхности равен нулю:  .Ответ «А». Напряженность поля в любой точке A, расположенной внутри проводника, равна нулю:  , где  - вектор, проведенный от бесконечно малой площадки поверхности проводника в точку A,  - заряд этой площадки. При увеличении в 2 раза суммарного заряда проводника электрическое поле в произвольной точке A внутри проводника останется равным нулю, если заряд каждой малой площадки поверхности проводника увеличится в 2 раза. Следовательно, поверхностная плотность заряда в каждой точке поверхности проводника увеличится в два раза. Опираясь на принцип суперпозиции, можно утверждать, что в каждой точке среды напряженность поля и потенциал также увеличатся в 2 раза.Ответ «В 4 раза». Внутри проводника напряженность поля равна нулю  , где  - напряженность поля точечного заряда q, а  - напряженность поля индуцированных на поверхности проводника зарядов. При увеличении заряда q в 2 раза, поле увеличивается в 2 раза, следовательно, и поле наведенных зарядов возрастает в 2 раза. Это означает, что заряд каждой малой площадки поверхности проводника должен увеличиться в 2 раза. Опираясь на закон Кулона и принцип суперпозиции, приходим к выводу, что сила взаимодействия точечного заряда и проводника увеличивается в 4 раза.Ответ «А». Перераспределение зарядов прекратится, когда потенциалы всех точек проводника (шар-проволока-шар) станут одинаковыми. В этом случае напряженность электрического поля внутри проводника равна нулю, поэтому равна нулю и сила, действующая на свободные носители заряда в проводнике. Ответ «В». Поток вектора индукции  через замкнутую поверхность определяется суммой сторонних зарядов, охватываемых этой поверхностью. Поскольку шар не заряжен, то потоки вектора  через поверхности «Б» и «В» равны нулю. Поток вектора напряженности через замкнутую поверхность определяется суммой всех зарядов (сторонних и связанных), охватываемых поверхностью. Внутри поверхности «Б» суммарный заряд равен нулю, т.к. диэлектрический шар не заряжен, а суммарный связанный заряд шара равен нулю. Внутри поверхности «В», включающей только часть диэлектрика, связанный заряд отличен от нуля.Ответ «А». Векторы  и вблизи границы раздела двух диэлектриков имеют одинаковые тангенциальные составляющие:  .Ответ «Б». Воспользуемся уравнениями  ,  ,которые выражают теоремы Гаусса для векторов 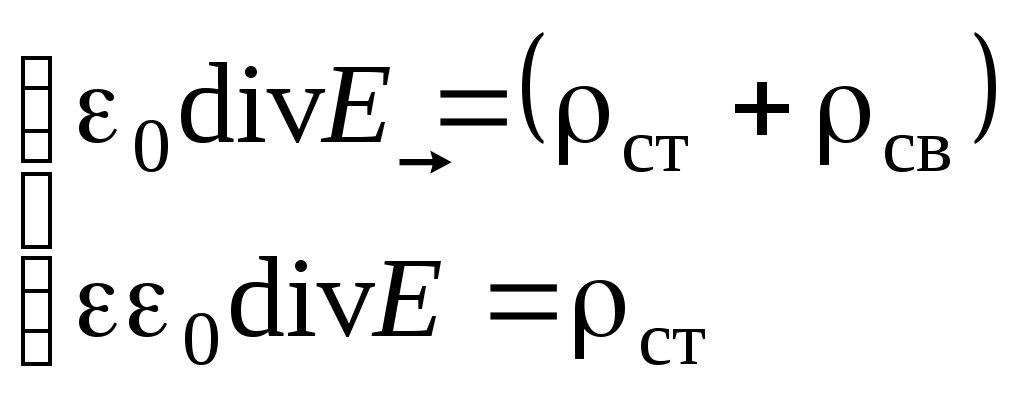и . Учитывая, что  и диэлектрическая проницаемость однородного диэлектрика не зависит от координаты, получим .После преобразований получим  .Ответ «А». Внутри поверхности S расположены сторонние и связанные заряды. При включении внешнего электрического поля может измениться только величина связанного заряда. Поскольку поток вектора равен стороннему заряду внутри поверхности, то этот поток при включении поля не изменится. Поток вектора , как это следует из теоремы Гаусса, зависит от суммы стороннего и связанного зарядов.Ответ «А», «Г». В системе из четырех точечных зарядов энергия взаимодействия равна сумме энергий парных взаимодействий зарядов системы. Таких пар шесть: четыре пары ближайших зарядов и две пары диагональных. Для заданных конфигураций получим:     Приравнивая объемные плотности энергии  , получим  .Ответ «А». Пусть C – емкость уединенного шара,  и  - значения электрической энергии для случаев А) и Б). Тогда ,  .Объемная плотность энергии электрического поля  положительна. Поэтому и полная электрическая энергия  всегда положительна (  , если электрическое поле отсутствует во всем пространстве).Ответ «Г». Электрическая энергия уединенного заряженного проводника определяется формулой  . Потенциал проводника имеет такой же знак, что и его заряд q, поэтому при любом знаке заряда q энергия  .По закону Ома для неоднородного участка цепи запишем:  . О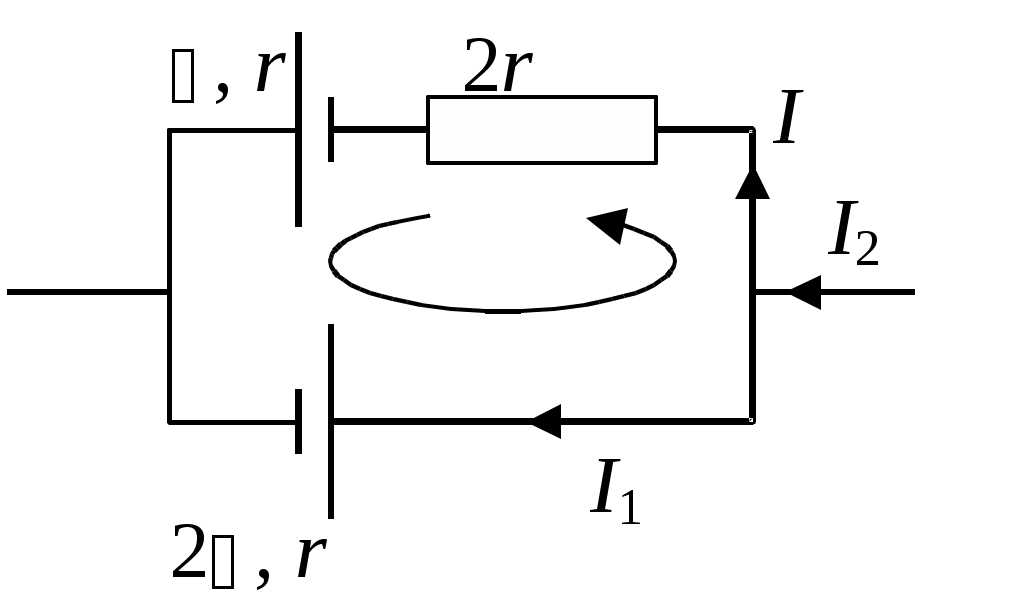тсюда найдем  –19 В.В  ыбирая направление обхода замкнутого контура и направление тока I через верхний источник, как показано на рисунке, запишем второе правило Кирхгофа: , откуда  6 А.Для «входного» узла цепи согласно первому правилу Кирхгофа найдем:  = 9 А.Сила тока через сечение провода равна  , где  - площадь поперечного сечения первого проводника, а  - второго. Следовательно  .Ответ «А». Сила Ампера, действующая на замкнутый контур с током со стороны однородного магнитного поля, всегда равна нулю:  , так как  . Момент сил Ампера равен нулю только в том случае, когда вектор магнитного момента контура с током параллелен вектору магнитной индукции.Ответ «Г». Используя закон Био-Савара, запишем   ,где вектор  проведен из точки K в точку L, а вектор – от рамки в точку A. Угол 1 между векторами и равен ; поэтому  .Аналогично найдем  ,где вектор  проведен из точки L в M, а  - угол между векторами и . Следовательно,  и  .Ответ «А». По закону Био-Савара индукция магнитного поля постоянного тока I, протекающего в замкнутом контуре L, определяется формулой 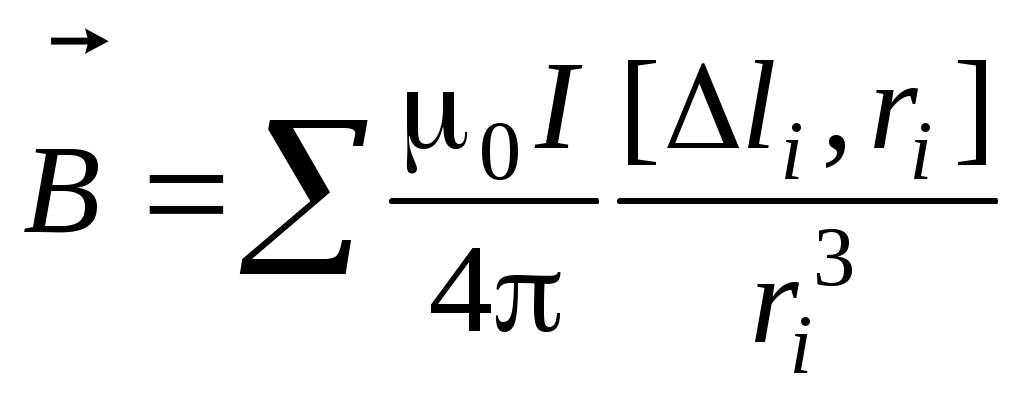 ,где  - бесконечно малый элемент длины контура, - вектор, проведенный от данного элемента в точку, где вычисляется магнитное поле. Эта формула и обосновывает выбор ответа.Ответ «А». Определим направление вектора  в одной из точек плоскости симметрии системы (см. рис.). Рассмотрим два случая: а) токи текут в одном направлении, б) направления токов противоположны. Из рисунков видно, что условию задачи соответствует случай одинаково направленных токов. Только в этом случае вектор направлен по касательной к заданным линиям поля .
Ответ «Б». Так как  , то  , где вектор  проведен из точки 1 в точку 3. Учитывая, что  , получаем ответ.Ответ «Б». В случае постоянных токов теорема о циркуляции вектора записывается в виде  , где  - ток через поверхность, ограниченную контуром L. Если ток I распределено по сечению провода однородно, то  . Отсюда получаем ответ.Ответ «А». С учетом симметрии распределения токов теорема о циркуляции вектора по замкнутому круговому контуру радиусаr запишется в виде: , где IГ – ток, пронизывающий контур: 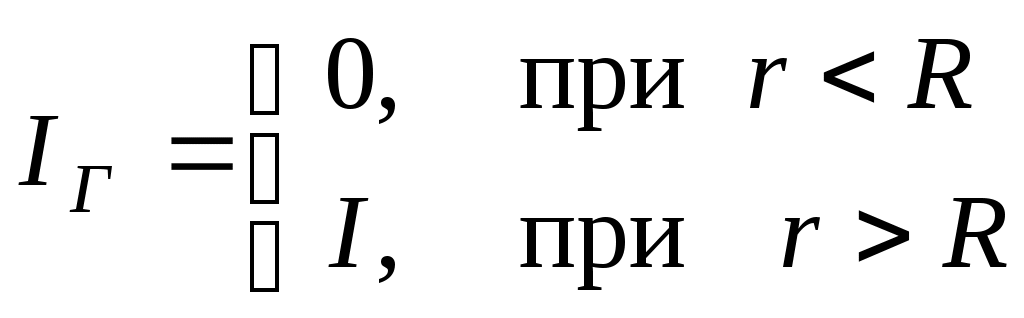 .Зависимость 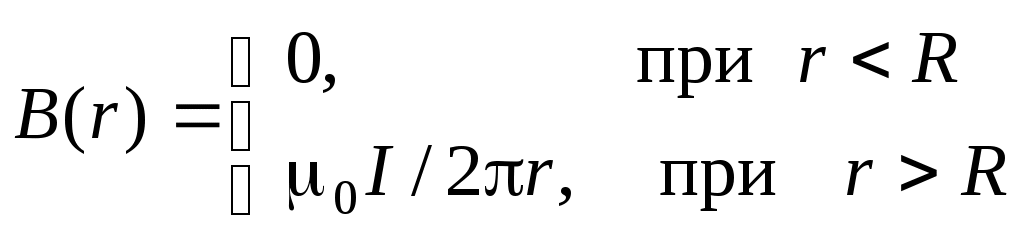 графически представлена на рис. «А». О 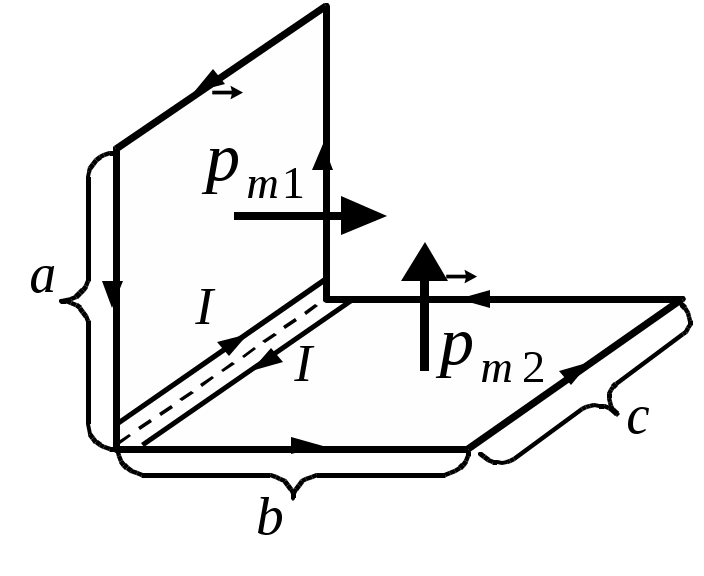 твет «А». Представим данный контур с током как эквивалентную суперпозицию двух плоских контуров, показанных на рисунке. Величины магнитных моментов равны  ,  , а их направления перпендикулярны. Магнитный момент всего контура равен  и учитывая перпендикулярность его составляющих, получим .Ответ «В». Ток I создает магнитное поле, вектор индукции которого в полуплоскости, где движется рамка, направлен «от нас» перпендикулярно плоскости чертежа. Направление нормали к поверхности, натянутой на рамку, также выберем «от нас». Выбранное направление нормали определяет направление обхода контура «по часовой». Из законов электромагнитной индукции и Ома следует  ,где R – сопротивление контура, Ф – магнитный поток. Ток в рамке положителен (то есть течет в направлении обхода – «по часовой»), если производная  . Это имеет место в случае «В», когда рамка перемещается в область более слабого магнитного поля, вследствие чего магнитный поток уменьшается.Ответ «Б». Из законов электромагнитной индукции и Ома следует , где R – сопротивление витка. Величина  максимальна, когда максимальна производная  . Ответ «Б». Циркуляция Г вектора напряженности электрического поля по произвольному замкнутому контуру в соответствии с уравнением Максвелла равна  , где  - магнитный поток через поверхность, ограниченную данным контуром. Выбранные на рисунке направления обходов контуров 1, 2, 3 определяют направления нормалей: «от нас» перпендикулярно плоскости чертежа. Учитывая, что поле прямого провода с током, изображенного на рисунке, слева от провода направлено «на нас», а справа от провода – «от нас», приходим к выводу, что  ,  ,  . С ростом тока I модули этих магнитных потоков возрастают, причем с наибольшей скоростью в ближайших к проводу контурах 1 и 2. Следовательно,  ,  .Ответ «А». Приравнивая объемные плотности энергии  , п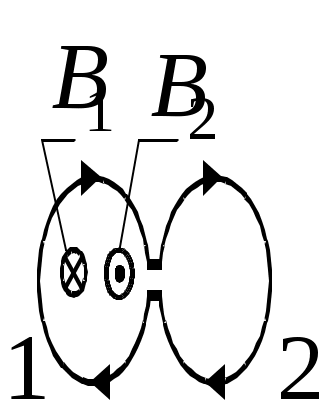олучим ответ.О  твет «В». Магнитное поле внутри витка-1 в его плоскости (см. рис.) можно представить в виде суммы  , где  - магнитное поле, созданное током в первом витке, а  - поле, созданное током, который протекает во втором витке. Направления векторов и можно определить при помощи закона Био-Савара. Магнитный поток через поверхность, ограниченную первым витком, равен .Учитывая, что и направлены противоположно, запишем .Для индуктивности контура, составленного из двух витков, получим  .Ответ «А». Переходной процесс описывается уравнением  . (1)В установившемся режиме  . Поскольку для первой катушки установившийся ток больше, то  . На начальной стадии переходного процесса в уравнении (1) можно считать  . Тогда  . Интегрируя это уравнение, получаем линейную зависимость тока от времени  . Из рисунка видно, что линейные участки графиков совпадают. Следовательно  .Ответ «А» следует из закона Ома для замкнутой цепи квазистационарного тока:  .Ответ «Б». Поскольку при выбранном направлении обхода положительный ток приводит к уменьшению заряда q обкладки-1 (ток «вытекает» из обкладки), то  .Интегрируя это уравнение  ,и подставляя численные значения и t, найдем  .Ответ «Б». Сравнивая данное уравнение с дифференциальным уравнением затухающих колебаний  , получаем  .Амплитуда затухающих колебаний зависит от времени экспоненциально:  . В рассматриваемом случае  . Отсюда  1000 с–1.Ответ «Б». Пусть  ,  и  - значения напряжения на конденсаторе в моменты времени  ,  и  , соответственно. Тогда ,  .Отсюда  ,  , и после преобразований получим ответ.Ответ «В». Из рисунка видно, что амплитуды токов в контурах 1 и 2 уменьшаются со временем t одинаково. Следовательно, равны коэффициенты затухания 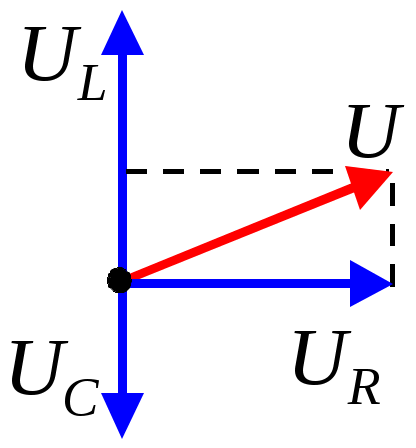 и  . Так как сопротивления контуров R1 и R2 одинаковы, то равны и их индуктивности: . Из рисунка также видно, что частота колебаний в первом контуре в несколько раз больше частоты во втором. Поскольку  , то   и, следовательно,  .Ответ «В». Ответ следует из векторной диаграммы (см. рис.). О 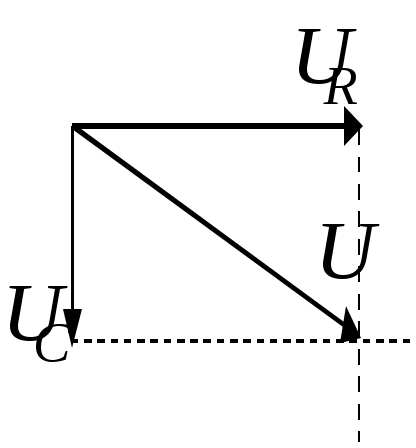 твет «В». По закону Ома для переменного тока: ,  , .Ответ можно также получить непосредственно из векторной диаграммы напряжений (см. рис.). Ответ: 200 Ом. Из формулы 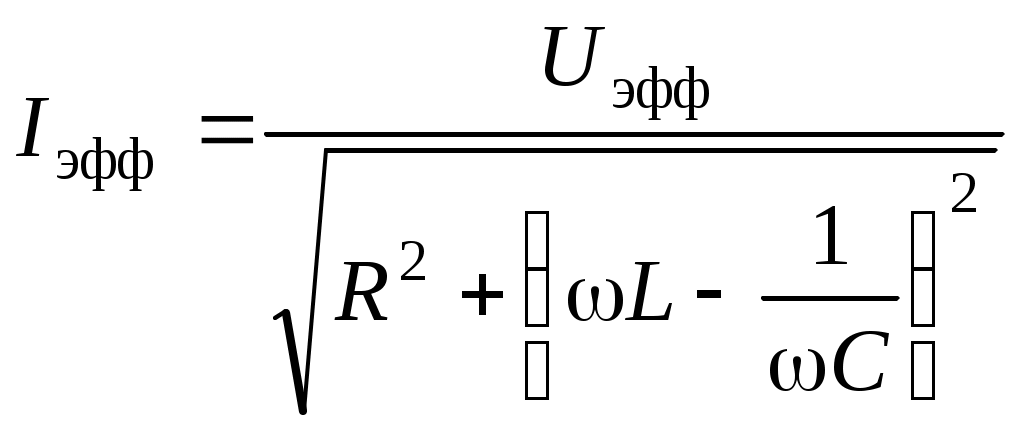 следует, что максимальное (резонансное) значение тока достигается при  и равно  . Из графика видно, что  = 6 мА. Следовательно,  200 Ом.Ответ «Б». В соответствии с уравнением Максвелла  циркуляция поля равна нулю, если поток  вектора магнитной индукции  через поверхность, ограниченную данным контуром, не зависит от времени.Ответ «Г» - в соответствии с уравнением Максвелла  .Составитель И.Н.Горбатый |
