Закон кулона Напряженность и потенциал электростатического поля и связь между ними. E Fq. E , ф e s e n ds теорема Остроградского Гаусса
 Скачать 320.86 Kb. Скачать 320.86 Kb.
|
|
Закон кулона 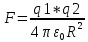 Напряженность и потенциал электростатического поля и связь между ними. E = F/q. E = 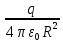 , , 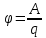 ФE = òSEndS ФE = òSEndS 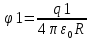 Теорема Остроградского - Гаусса. 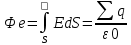 Работа по перемещению заряда. Энергия электрического поля dA = (Fdl) = Fdl*cosa = (1/4pe0)(qq0/r2)dlcosa. 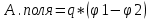 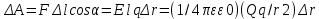 Элктроемкость C = q/Δφ = σS/Ed = ε0S/d. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз: C = εε0S/d C = (4πεε0) (R1R2)/(R2 – R1) (сферический конденсатор) C = (2πεε0) L/(lnR2/R1) (цилиндрический конденсатор). Энергия элктрического поля 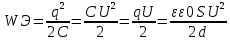 Определение индукции магнитного поля 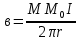 Сила ампера 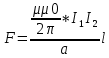 Движение заряженных частиц в электрическом и магнитном полях 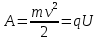 q.v.B = m.v2/rоткуда r = (m/q).(v/B). Период вращения частицы, т.е. время, затрачиваемое частицей на один полный оборот, Т = (2pr/v) = (2p/B)*(m/q), v|| = v.cosa v^ = v.sina Электромагнитная индукция Ei = - dФ/dt Переменный ток Переменный ток — это, изменяющий периодически свое направление в цепи таким образом, что среднее его значение за период Т равно нулю. Простейший переменный ток имеет вид: I = I0 sin(t + ), (14.2.) где I0-амплитуда, = 2Т- (14.3.) круговая частота и -начальная фаза. Переменный ток получают, вращая равномерно плоскую рамку в магнитном поле. Магнитный поток при этом меняется Ф = Фmax.cos t = B.S.cos t. dB — магнитная индукция поля, создаваемого элементом проводника с током;F/I∆l - магнитная проницаемость B/B0 0 - магнитная постоянная (0 = 4.10–7 Гн/м) В - магнитная индукция поля [Тесла/Тл] L – индуктивность [Генри/Гн] С – электроемкость [Фарад/ф] Ф – магнитный поток [Вебер/Вб] - диэлектрическая проницаемость период колебаний с - скорость электромагнитных волн в вакууме (с = 3.108 м/с). - диэлектрическая проницаемость; i - электродвижущая сила индукции; сила Лоренца - cила F, действующая на заряд q формулой F = q[vB] или F = |q|vBsin Закон Ампера. Сила, действующая на проводник с током в магнитном поле F= BIl sin, Закон Био - Савара – Лапласа dB = (0/4)(Isin/r2)dl, где - угол между векторами dl и г. Работа по перемещению контура с током в магнитном поле А = IФ Основной закон электромагнитной индукции (закон Фарадея — Максвелла) i = - N(dФ/dt) = - d/dt, где N - число витков контура; - потокосцепление.   МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА. МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА.2. Магнитная индукция В связана с напряженностью Н магнитного поля В = 0Н 3. Магнитная индукция в центре кругового проводника с током B = (0/2)(I/R), где R – р. кривизны 4. Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током, В = (0/2)(I/r), г – расст от оси. Магнитная индукция поля, создаваемого отрезком проводника, В = (0/4)(I/r0)(cos1 - cos2). При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция - cos2 = cos1 = cos и, следовательно, B = (0/2)(I/r0)cos. 5. Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси), В = 0nI, где n - число витков, приходящихся на единицу длины соленоида; I - сила тока в одном витке. 6. Принцип суперпозиции магнитных полей: магнитная индукция В результирующего поля равна векторной сумме магнитных индукций B1, B2, ., Bn, складываемых полей, т. е. B = Bi. В частном случае наложения двух полей В = B1 + B2, В = B12 + B22 + 2B1B2 cos, СИЛА, ДЕЙСТВУЮЩАЯ НА ПРОВОДНИК С ТОКОМ В МАГНИТНОМ ПОЛЕ. 2. Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга, рассчитанная на отрезок проводника длиной l, выражается формулой F = (0/2)(I1I2/d)l. 3. Магнитный момент контура с током Pm = IS, где S – площадь охватываемой контуром, и совпадающий по направлению с нормалью к его плоскости. 4. Механический момент, действующий на контур с током, помещенный в однородное магнитное поле, М = [pmВ]. Модуль механического момента М = pmBsin, где - угол между векторами рm и В. 5. Потенциальная (механическая) энергия контура с током в магнитном поле П мех. = pmВ = pmBcos. 6. Сила, действующая на контур с током в магнитном поле (изменяющемся вдоль оси х), F = pm(B/x)cos, где (B/x) - изменение магнитной индукции вдоль оси Ох, рассчитанное на единицу длины; -угол между векторами рm и ЗАКОН ПОЛНОГО ТОКА. МАГНИТНЫЙ ПОТОК. МАГНИТНЫЕ ЦЕПИ. 1. Циркуляция вектора магнитной индукции В вдоль замкнутого контура Bidl, где Bi - проекция вектора магнитной индукции на направление элементарного перемещения dl вдоль контура L. Циркуляция вектора напряженности Н вдоль замкнутого контура Hidl. 2. Закон полного тока (для магнитного поля в вакууме) Bidl = 0Ii, где - магнитная постоянная; Ii - алгебраическая сумма токов, охватываемых контуром; n - число токов. Закон полного тока (для произвольной среды) Hidl = Ii. Магнитный поток Ф через плоский контур площадью S: а) в случае однородного поля Ф = BS cos б) в случае неоднородного поля Ф = BndS где интегрирование во всей поверхности S. 3. Потокосцепление, т. е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида, = nФ, n – число витков 4. Магнитное поле тороида, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями: а) магнитная индукция на осевой линии тороида В = (In)/[l1/01) + l2/(82) n - число витков; l1и l2 - длины частей сердечника тороида; 1 и 2 - магнитные проницаемости веществ частей сердечника б) напряженность магнитного поля на осевой линии тороида в первой и второй частях сердечника H1 = B/(10); H2 = B/(20); в) магнитный поток в сердечнике тороида Ф = (IN)/[l1/(10S) + l2/(20S) 5. Магнитная проницаемость ферромагнетика связана с магнитной индукцией В поля в нем и напряженностью Н намагничивающего поля соотношением = B/(0H). РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ИНДУКТИВНОСТЬ. Работа по перемещению замкнутого контура с током в магнитном поле А = IФ, где Ф - изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I - сила тока в контуре. 2. Основной закон электромагнитной индукции (закон Фарадея — Максвелла) i = - N(dФ/dt) = - d/dt, где i - электродвижущая сила индукции; N - число витков контура; - потокосцепление. Частные случаи применения основного закона электромагнитной индукции: а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью v в однородном магнитном поле, U = Blvsin, где - угол между направлениями векторов скорости v и магнитной индукции В; б) электродвижущая сила индукции i, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью в магнитном поле с индукцией В i = BNSsint, где t - мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки. 3. Количество электричества Q, протекающего в контуре, Q = Ф/R, где R - сопротивление контура; Ф - изменение потокосцепления. 4. Электродвижущая сила самоиндукции i, возникающая в замкнутом контуре при изменении силы тока в нем, i = - L(dI/dt), или i = - L(I/t), где L - индуктивность контура. 5. Потокосцепление контура = LI, где L - индуктивность контура. 6. Индуктивность соленоида (тороида) L = 0n2V. 7. Мгновенное значение силы тока I в цепи а) после замыкания цепи I = (/R)(1 – e –(R/L)t), t - время, прошедшее после замыкания цепи; б) после размыкания цепи I = I0e –(R/L)t), где I0 - сила тока в цепи при t = 0; t - время, прошедшее с момента размыкания цепи. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. 8. Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L: W = (1/2)LI 2 9. Объемная (пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида) = (0/2)H2 = (1/20)B2. 10. Формула Томсона. Период собственных колебаний в контуре без активного сопротивления T = 2LC, 11. Связь длины электромагнитной волны с периодом T и частотой колебаний = cT или = c/, 12. Скорость электромагнитных волн в среде v = c/, 1 вариант Конденсаторы. Устройства, обладающие способностью накапливать значительные заряды, называются конденсаторами. Обычный конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками. 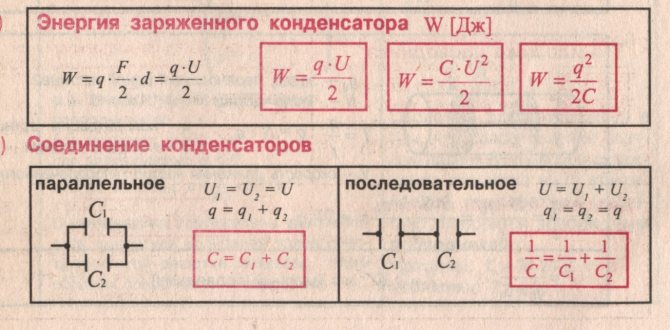 Закон ампера. Магнитное поле оказывает на рамку с током ориентирующее (вращающее) действие. Ампер установил, что сила dF, действущая на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорционально силе тока I в проводнике и векторному произведению элемента длиной dl на магнитную индукцию В: dF = I.[dl.B]. dF = I.B.dl.sina  2 вариант Электропроводность в различных агрегатных состояниях. Электропроводность газообразных диэлектриков связана с наличием в них заряженных частиц (ионов, электронов, взвешенных жидких и твердых заряженных частиц). В обычном состоянии газы обладают очень малой проводимостью. В жидкостях электропроводность сильно зависит от двух основных причин: 1) наличия примесей; 2) строения молекул (неполярная или полярная). Самоиндукция Самоиндукция является случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Ei = - dФ/dt = - d(L.I)/dt Определить добротность и частоту колебательного контура,состоящего из катушки индуктивностью 5 мГн и конденсатора емкостью 10нФ .Сопротивление контура 2 Ом. Дано: L = 5*10^(-3) Гн, C = 10^(-8) Ф, R = 2 Ом. Резонансная круговая частота колебаний ωо = Добротность колебательного контура определяется по формуле: 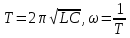 3 вариант Циркуляция вектора напряженности электростатического поля. Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L 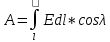 Если работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю. Сила лоренца 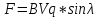 Колебательный контур состоит из индуктивности l и емкости c, в емкости заменили диэлектрик 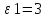 на дижлектрик на дижлектрик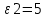 . Найти во сколько раз именилась собственная частота контура. . Найти во сколько раз именилась собственная частота контура. Вариант 6 Электроемкость проводника. Емкость конденсатора равна отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j1 - j2) между его обкладками: C = Q/(j1 - j2) = q/Δφ = q/U. Магнитная индукция. 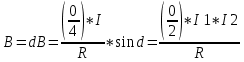 ХЗ Вариант 10 1. Напряженность электростатического поля. Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда: E = F/q. 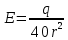 Трансформаторы. Принцип работы трансформатора основан на явлении электромагнитной индукции Фарадея: переменное напряжение, подключенное к первичной обмотке, вызывает в ней переменный ток, который в свою очередь создает вокруг обмотки переменное магнитное поле, в находящейся в этом поле вторичной обмотке индуктируется ЭДС, пропорциональная числу витков обмотки. Если в первичной обмотке число витков меньше - то это повышающий трансформатор, если наоборот, то речь идет о понижающем трансформаторе. Какая работа необходима для перемещения точечного заряда q из бесконечности в точку на расстоянии l от поверхности шара радиусом R зарядом Q. Решение: Работа сил поля по перемещению заряда из точки поля с потенциалом 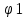 в точку с потенциалом в точку с потенциалом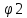 . . 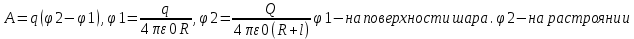 Вариант 16 1. Энергия электростатического поля. 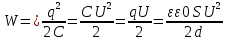 Преобразуем формулу, выражающую энергия плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора (С = e0eS/d) и разности потенциалов между его обкладками (Dj = Ed). Тогда 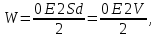 2. Эффектом Холла называется возникновение поперечного электрического поля и разности потенциалов в проводнике или полупроводнике, по которым проходит электрический ток, при помещении их в магнитное поле, перпендикулярное к направлению тока. Если в магнитное поле c индукцией В поместить проводник или электронный полупроводник, по которому течет электрический ток плотности j, то на электроны, движущиеся со скоростью V в магнитном поле, действует сила Лоренца F, отклоняющая их в определенную сторону. |
