Подземная гидромеханика. Закон (опыт Дарси) Производилась фильтрация жидкости через песок
 Скачать 11.3 Kb. Скачать 11.3 Kb.
|
|
1 Линейный и нелинейные законы фильтрации Линейный закон (опыт Дарси) - Производилась фильтрация жидкости через песок. Линейный закон фильтрации применим к ламинарному движению жидкости Q = KфF*ΔH/ΔL где Q — расход потока; Кф — коэффициент фильтрации; F — площадь поперечного сечения потока; ΔН — перепад напоров; ΔL — длина участка фильтрационного потока Линейный закон фильтрации применим тогда, когда зависимость между градиентом давления и расходом флюида имеет линейный характер. Нарушение линейного закона фильтрации сильнее всего проявляется в призабойной зоне пласта, где наибольшие скорости фильтрации. Нелинейный закон фильтрации. – зависимость между gradP и скоростью фильтрации нелинейная.  где с –скоростной коэффициент; n –показатель закона фильтрации. Есть еще Двучленная формула нелинейного закона фильтрации:  где i – гидравлический уклон, a и b – экспериментальные константы, υ – скорость фильтрации 2 Границы применимости линейного закона. Т.к. линейный закон фильтрации всё-таки является приближенным законом, при увеличении скорости фильтрации жидкости и соответствующем увеличении скоростного напора сделанное ранее при выводе линейного закона фильтрации допущение может оказаться несправедливым, тогда и возникнут погрешности в расчетах. Исходя из этого линейный закон фильтрации имеет верхнюю и нижнюю границы применения. Верхняя граница определяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением числа Рейнольдса. Нижняя границаопределяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействия с твердым скелетом пористой среды при достаточно малых скоростях фильтрации. 3. Уравнение притока жидкости в скважине (ф. Дюпюи) 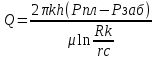 Q – дебит скважины k – проницаемость пласта h – толщина пласта Pпл – пластовое дав-е Рзаб – забойное дав-е μ – вязкость жидкости Rк – радиус контура питания rс – радиус контура скв. 4 Модели фильтрацилнных потоков (прямолинейно-параллельный, плоскорадиальный, радиально сферический фильтрационный поток) Прямолинейно-параллельный поток. Траектории всех частиц жидкости – паралельные прямые, а скорости фильтрации во всех точкахлюбого поперечного сечения потока равны меджу собой. Прямолинейно-параллельный поток имеет место в лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполенную пористой средой. Плоскорадиалный поток. Траектории всех частиц жидкости прямолинейные горизонтальные прямые, радиально сходящие к центру скв., а скорости фильтрации во всех точках любого поперечного сечения потока параллельны и равны между собой. Радиально сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящие к центру полусферического забоя, скорость фильрации в любой точке потока явл-ся функцией растсояния этой точки от центра забоя. 5 Воронка депрессии, уравнение распределения по пласту (плоскорадиальный поток) Воронка депрессии - зона резкого снижения давления в пласте вокруг действующей добывающей скважины. В пределах воронки депрессии градиенты давления, а значит и расходы энергии на единицу длины пути резко возрастают по мере приближения к скважине. Значительная доля перепада давления в пласте расходуется в непосред-й близости от скважины. По мере удаления от скв. кривые градиентов давления значительно выравниваются, что указывает на резкое уменьшение скорости фильтрации с удалением от скв. В процессе работы вокруг каждой скв. образуется воронка депрессии. Воронки имеют неправильные формы, пересекаются между собой. Если бы пласт был идеально однородным и разбурен равномерной сеткой скв и они работали бы с одинаковыми дебетами, то радиусы всех воронок были бы одинаковыми и раснялись бы половине расстояния между скв. На практике принято считать радиус воронки вокруг скв. равным половине среденего расстояния данной скв. от ближних скв. Принято называть это расстояние условным контуром влияния скважины. Если известно Рпл. на контуре питания скв., значит актуальна формула Дюпюи для плоскорадиального притока жидкости в скважину. 6 Коэффициент продуктивности, уравнение, индикаторная диаграмма.  rспп – приведенный радиус Коэффициент продуктивности определяется в рез-те исследования скв. при установившихя отборах. Коэффициент продуктивности определяется по результатам гидродинамических исследований и эксплуатации скважин. Далее используя замеры строят индикаторные диаграммы, представляющие собой зависимость дебита от Рзаб. или от перепадов между Рзаб. и Рпласт. По наклону индикаторной линии определяют фактическую продуктивность. 7 Интерференция скважин. Интерференция скважин - это взаимное влияние скв. друг на друга. Это влияние приводит к тому что при вводе в экспл-ю новых скв. суммарная добыча на месторождении растет медленее чем увеличивается количество скв. 8 Понятие о призабойной зоне пласта, скин фактор, скин эффект Призабойная зона пласта – участок пласта примыкаюший к стволу скв., в пределах которого в процессе добычи происходит наибольшее изменение давления ввиду увеличения гидродинамического соротивления, связанного с изменением направления движения фильтрационных потоков и изменению фильтрационных характеристик продуктивного пласта. Скин фактор гидродин-й параметр характер-й дополнительное фильтрац-е сопротивленние течению флюидов в околоскв-й зоне пласта и приводящее к изменению дообычи. Скин фактор – наличие или отсут-е дополнтельных фильтрационных сопротивлений в призабоной зоне. Явление изменения проницаемости призабойной зоны обусловленое вскрытим пласта в процессе бурения и освоения скв. называется скин эффектом |
