распад. Документ Microsoft Word. Закон радиоактивного распада править
 Скачать 122.49 Kb.
|
Закон радиоактивного распада[править | править код] Материал из Википедии — свободной энциклопедии Перейти к навигацииПерейти к поиску
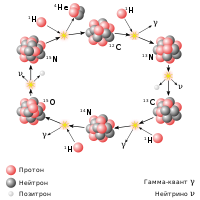
Основная статья: Радиоактивный распад Зако́н радиоакти́вного распа́да — физический закон, описывающий зависимость интенсивности радиоактивного распада от времени и от количества радиоактивных атомов в образце. Открыт Фредериком Содди и Эрнестом Резерфордом, каждый из которых впоследствии был награждён Нобелевской премией. Они обнаружили его экспериментальным путём и опубликовали в 1903 году в работах «Сравнительное изучение радиоактивности радия и тория»[1] и «Радиоактивное превращение»[2], сформулировав следующим образом[3]: Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии. из чего с помощью теоремы Бернулли учёные сделали вывод[4]: Скорость превращения всё время пропорциональна количеству систем, ещё не подвергнувшихся превращению. Существует несколько формулировок закона, например, в виде дифференциального уравнения: ����=−��,  которое означает, что число распадов −dN, произошедшее за короткий интервал времени dt, пропорционально числу атомов N в образце.  Содержание1Экспоненциальный закон 2Характеристики распада 2.1Среднее время жизни 2.2Период полураспада 3Примеры характеристик распада 4Интересные факты 5Примечания Экспоненциальный закон[править | править код]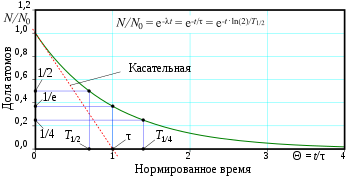 Экспоненциальная кривая радиоактивного распада: по оси абсцисс («оси x») — нормированное время Θ=�/�, по оси ординат («оси y») — доля �/�0 ещё нераспавшихся ядер или скорость распада в единицу времени I(�)=��/�Θ В указанном выше математическом выражении неотрицательная константа � — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с−1. Знак минус указывает на убыль числа радиоактивных ядер со временем.Решение этого дифференциального уравнения имеет вид: �(�)=�0�−��, где �0 — начальное число атомов, то есть число атомов для �=0. Таким образом, число радиоактивных атомов уменьшается со временем по экспоненциальному закону. Скорость распада, то есть число распадов в единицу времени: I(�)=−����, также падает экспоненциально. Дифференцируя выражение для зависимости числа атомов от времени, получаем: I(�)=−���(�0�−��)=��0�−��=I0�−��, где I0 — скорость распада в начальный момент времени �=0. Таким образом, зависимость от времени числа нераспавшихся радиоактивных атомов и скорости распада описывается одной и той же постоянной � [4][5][6][7].Характеристики распада[править | править код] Наглядная демонстрация закона. Кроме константы распада �, радиоактивный распад характеризуют ещё двумя производными от неё константами, рассмотренными ниже.Среднее время жизни[править | править код]Основная статья: Время жизни Из закона радиоактивного распада можно получить выражение для среднего времени жизни радиоактивного атома. Число атомов, в момент времени � претерпевших распад в пределах интервала �� равно −��, их время жизни равно −���. Среднее время жизни получаем интегрированием по всему периоду распада:�=−1�0∫�00���=�∫0∞��−����=1�. Подставляя эту величину в экспоненциальные временные зависимости для �(�) и I(�), легко видеть, что за время � число радиоактивных атомов и активность образца (количество распадов в секунду) уменьшаются в e раз[4].Период полураспада[править | править код]Основная статья: Период полураспада На практике получила большее распространение другая временная характеристика — период полураспада �1/2, равная времени, в течение которого число радиоактивных атомов или активность образца уменьшаются в 2 раза[4].Связь этой величины с постоянной распада можно вывести из соотношения �(�1/2)�0=�−��1/2=1/2, откуда:�1/2=ln2�=�ln2≈0,693�. Примеры характеристик распада[править | править код]Существующие в природе радиоактивные изотопы в основном возникают в сложных цепочках распадов урана и тория и имеют периоды полураспада в очень широкой области значений: от 3⋅10−7 секунды для 212Po до 1,4⋅1010 лет для 232Th. Наибольший экспериментально измеренный период полураспада имеет изотоп теллура 128Te — 2,2⋅1024 лет. Само существование в настоящее время многих естественных радиоактивных элементов несмотря на то, что с момента образования этих элементов при звёздном нуклеосинтезе прошло более 4,5 млрд лет, является следствием очень больших периодов полураспада 235U, 238U, 232Th и других природных радионуклидов. К примеру, изотоп 238U стоит в начале длинной цепочки (так называемый ряд радия), состоящей из 20 изотопов, каждый из которых возникает при α-распаде или β-распаде предыдущего элемента. Период полураспада 238U (4,5⋅109 лет) много больше, чем период полураспада любого из последующих элементов радиоактивного ряда, поэтому распад в целом всей цепочки происходит за то же время, что и распад 238U, её родоначальника, в таких случаях говорят, что цепочка находится в состоянии секулярного (или векового) равновесия[7]. Примеры характеристик распада некоторых веществ[8]:
Интересные факты[править | править код]Один из открывших закон, Фредерик Содди, в своей научно-популярной книге «The story of atomic energy», изданной в 1949 году, видимо из скромности, ничего не пишет о своём (но и чьём-либо ещё тоже) вкладе в создание этой теории, зато довольно оригинально отзывается о ней[11][12]: Следует отметить, что закон превращений одинаков для всех радиоэлементов, являясь самым простым и в то же время практически необъяснимым. Этот закон имеет вероятностную природу. Его можно представить в виде духа разрушения, который в каждый данный момент наугад расщепляет определённое количество существующих атомов, не заботясь об отборе тех из них, которые близки к своему распаду. Примечания[править | править код]↑ Rutherford E. and Soddy F. A comparative study of the radioactivity of radium and thorium (англ.) // Philosophical Magazine Series 6 : journal. — 1903. — Vol. 5, no. 28. — P. 445—457. — doi:10.1080/14786440309462943. ↑ Rutherford E. and Soddy F. Radioactive change (неопр.) // Philosophical Magazine Series 6. — 1903. — Т. 5, № 29. — С. 576—591. — doi:10.1080/14786440309462960. ↑ Кудрявцев П. С. Открытие радиоактивных преврещений. Идея атомной энергии // Курс истории физики. — 1982. Архивировано 23 ноября 2010 года. ↑ Перейти обратно:1 2 3 4 Климов А. Н. Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 74—75. — 352 с. Архивировано 23 сентября 2020 года. ↑ Бартоломей Г. Г., Байбаков В. Д., Алхутов М. С., Бать Г. А. Основы теории и методы расчета ядерных энергетических реакторов. — М.: Энергоатомиздат, 1982. ↑ Cameron I. R. Nuclear fission reactors. — Canada, New Brunswick: Plenum Press, 1982. ↑ Перейти обратно:1 2 Камерон И. Ядерные реакторы. — М.: Энергоатомиздат, 1987. — С. 320. ↑ Пособие по физике реактора ВВЭР-1000. — БАЭС, ЦПП, 2003. ↑ Wang M., Audi G., Kondev F. G., Huang W. J., Naimi S., Xu X. The Ame2016 atomic mass evaluation (I). Evaluation of input data; and adjustment procedures (англ.) // Chinese Physics C. — 2016. — Vol. 41, iss. 3. — P. 030002-1—030002-344. — doi:10.1088/1674-1137/41/3/030002. ↑ Wang M., Audi G., Kondev F. G., Huang W. J., Naimi S., Xu X. The Ame2016 atomic mass evaluation (II). Tables, graphs, and references (англ.) // Chinese Physics C. — 2016. — Vol. 41, iss. 3. — P. 030003-1—030003-442. — doi:10.1088/1674-1137/41/3/030003. ↑ Frederick Soddy, F.R.S. The story of atomic energy. — London: Nova Atlantis, 1949. ↑ Содди Ф. История атомной энергии. — М.: Атомиздат, 1979. — С. 288.
|
