Основные законы распределения случайных величин. Закон распределения
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Основные законы распределения случайных величин 1. Биномиальный закон распределения Вернемся к схеме независимых испытаний и найдем закон распределения случайной величины Х – числа появлений события А в серии из п испытаний. Возможные значения А: 0, 1, …, п. Биномиальным законом распределения называется распределение вероятностей дискретной случайной величины X = k - числа появлений события в n независимых испытаниях, описываемое формулой Бернулли: 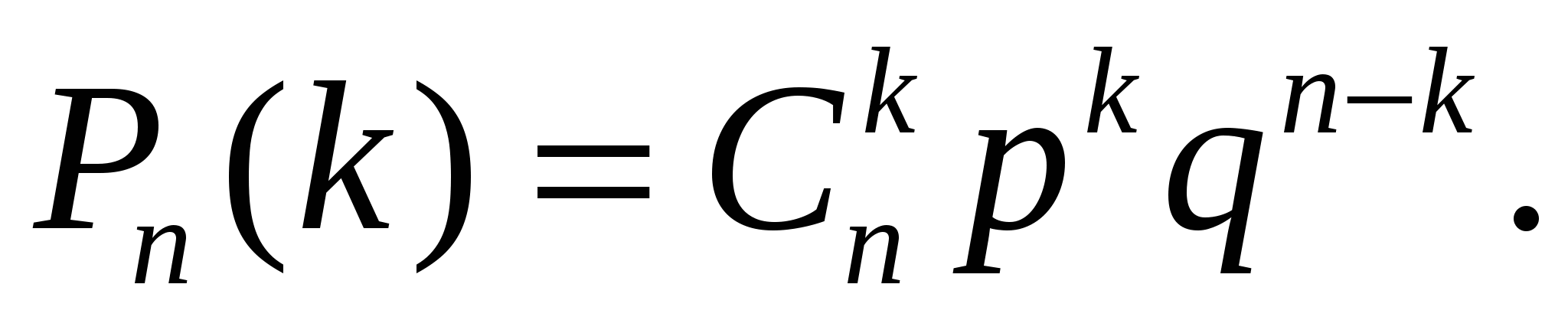 Ряд распределения биномиального закона имеет вид
Пример 1. Составим ряд распределения случайной величины Х – числа попаданий при 5 выстрелах, если вероятность попадания при одном выстреле равна 0,8. Решение. р(Х=0) = 1·(0,2)5 = 0,00032; р(Х=1) = 5·0,8·(0,2)4 = 0,0064; р(Х=2) = 10·(0,8)2·(0,2)3 = 0,0512; р(Х=3) = 10·(0,8)3·(0,2)2 = 0,2048; р(Х=4) = 5·(0,8)4·0,2 = 0,4096; р(Х=5) = 1·(0,8)5 = 0,32768. Таким образом, ряд распределения имеет вид:
Справедливы теоремы: 1. При биномиальном распределении математическое ожидание (среднее значение) числа появлений события равно произведению числа испытаний на вероятность p появления события в одном испытании M(X) = np, а дисперсия равна D(X) = npq. 2. Наивероятнейшее число появлений события в n независимых испытаниях (такое число k, которое при данном n имеет наибольшую вероятность ) удовлетворяет двойному неравенству np - q < k < np + p . Если (np – q) - дробное число, то существует единственное значение k*, если (np – q) - целое число, то k* может принимать два значения. Пример 2. Произведено 6 выстрелов по цели. Вероятность промаха при каждом выстреле одинакова и равна 0,4. Найти наивероятнейшее число попаданий и его вероятность; вероятность разрушения цели, если для этого требуется не менее двух попаданий. Решение. Каждый выстрел можно рассматривать как отдельное независимое испытание. Поэтому применима схема повторяющихся независимых испытаний. По условию n = 6, p = 0,6; q = 0,4. Поэтому np - q = 3,2; np + p = 4,2. Следовательно, k = 4. Вероятность 4-x попаданий равна 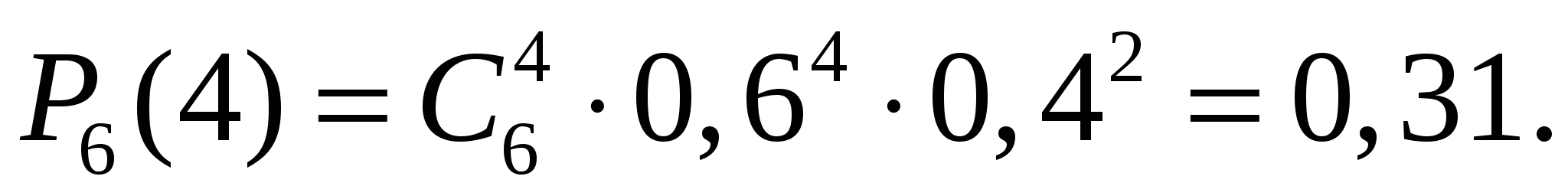 Пусть A - событие, состоящее в том, что будет не менее двух попаданий при 6 выстрелах. Удобно перейти к противоположному ему событию Очевидно, 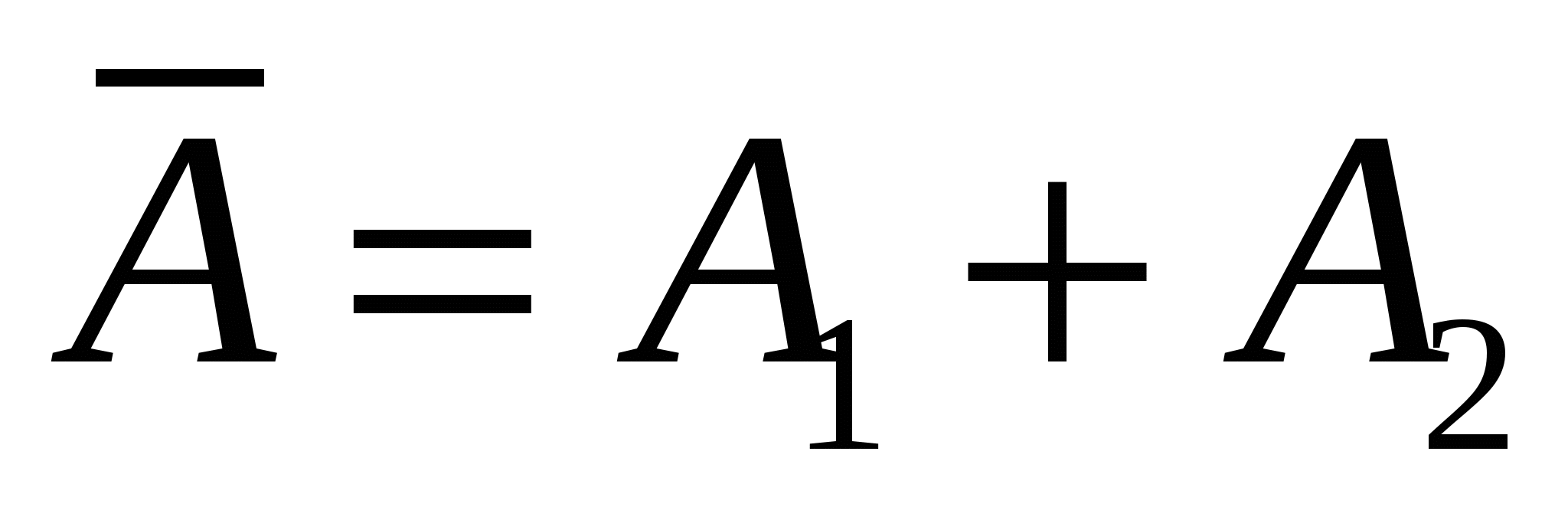 . .Так как события Искомая вероятность 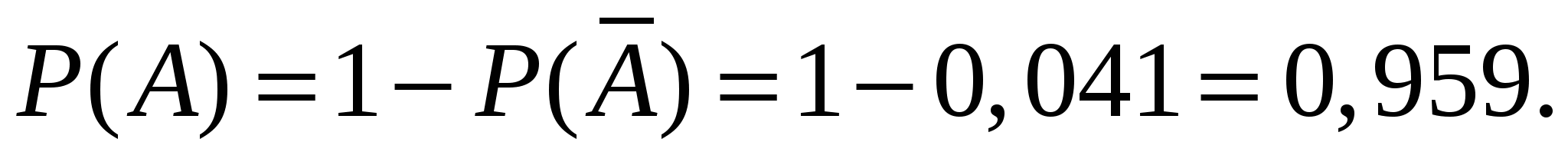 Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний, М(Х) можно найти, используя свойство 4 математического ожидания. Пусть Х1 – число появлений А в первом испытании, Х2 – во втором и т.д. При этом каждая из случайных величин Хiзадается рядом распределения вида
Следовательно, М(Хi) = p. Тогда 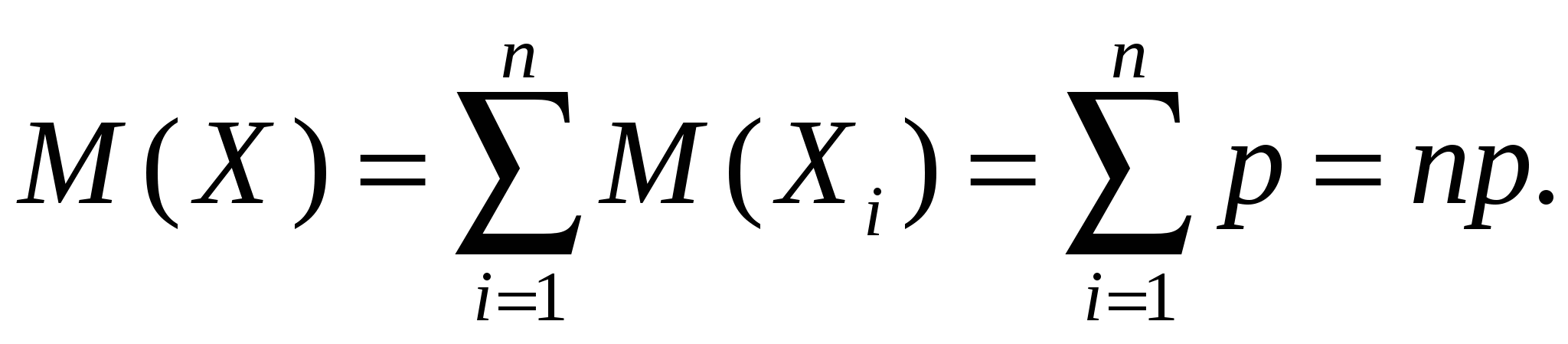 Аналогичным образом вычислим дисперсию: D(Xi) = 0²·q + 1²·p – p²= p – p² = p(1 – p), откуда по свойству 4 дисперсии 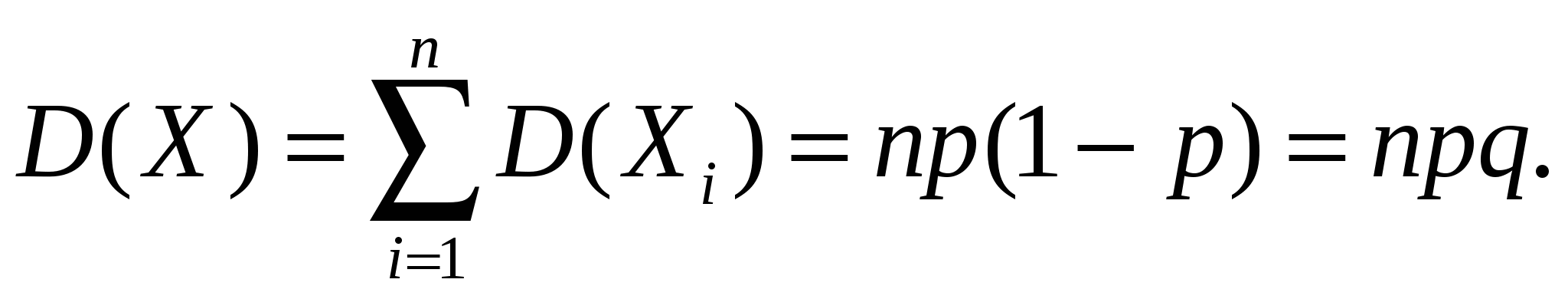 2. Закон распределения Пуассона Рассмотрим дискретную случайную величину Х, принимающую только целые неотрицательные значения (0, 1, 2,…, т,…), последовательность которых не ограничена. В предельном случае биномиального распределения, когда число испытаний n очень велико, а вероятность появления события в каждом отдельном испытании очень мала, вероятность появления события k раз в n независимых испытаниях может быть определена по приближенной формуле 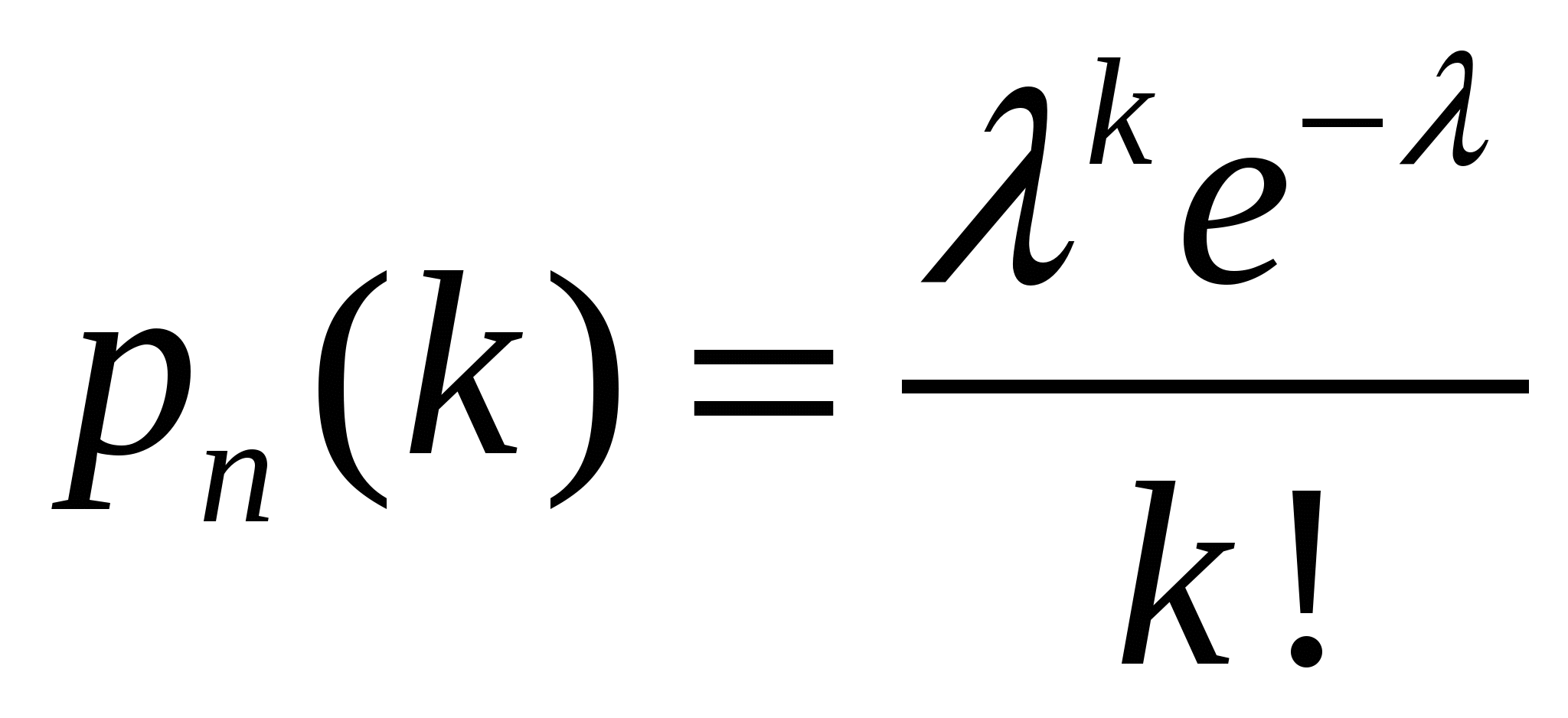 , , где 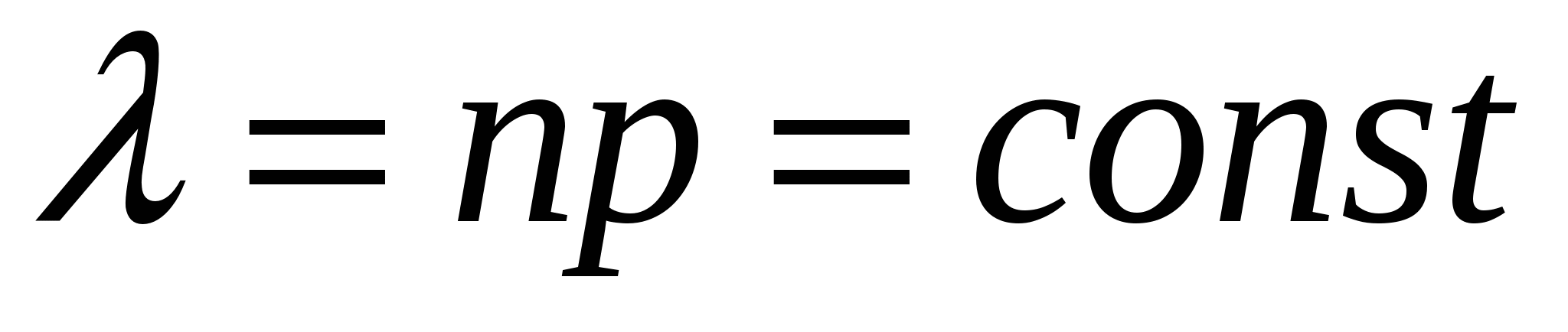 - среднее число появлений события в различных сериях испытаний, предполагаемое постоянным. - среднее число появлений события в различных сериях испытаний, предполагаемое постоянным.Эта формула выражает закон распределения вероятностей дискретной случайной величины k - числа появлений события в n независимых испытаниях (в случае массовых, но редких событий ), называемый законом распределения Пуассона. Замечание. Практически формулой Пуассона с достаточной степенью точности можно пользоваться при p < 0,1; Замечание. Таким образом, обнаружено интересное свойство распределения Пуассона: математическое ожидание равно дисперсии (и равно единственному параметру 3. Геометрическое распределение Пусть производится ряд независимых испытаний (”попыток”) для достижения некоторого результата (события где Вероятности 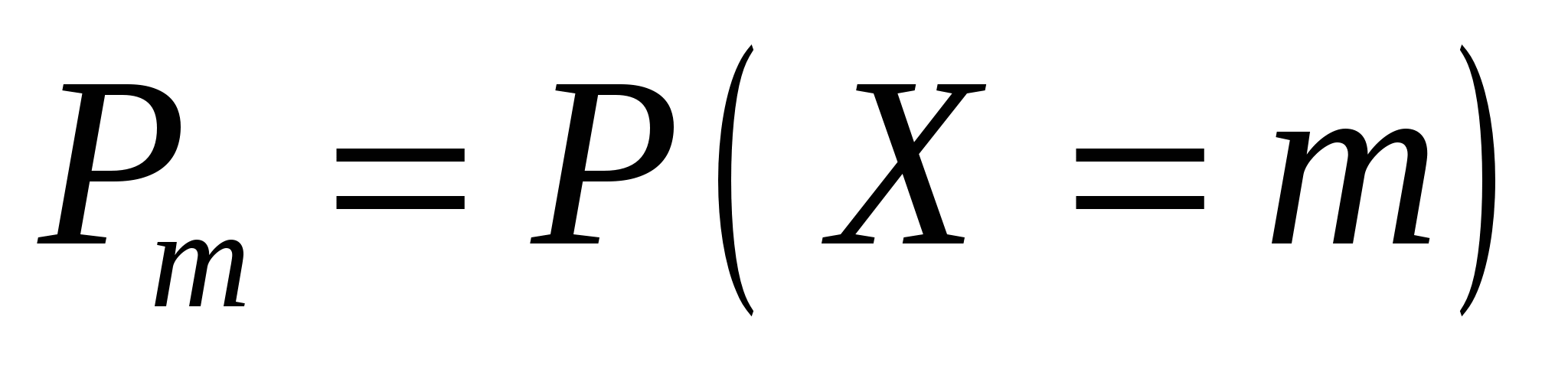 образуют для ряда последовательных значений образуют для ряда последовательных значений Ряд распределения
Математическое ожидание и дисперсия 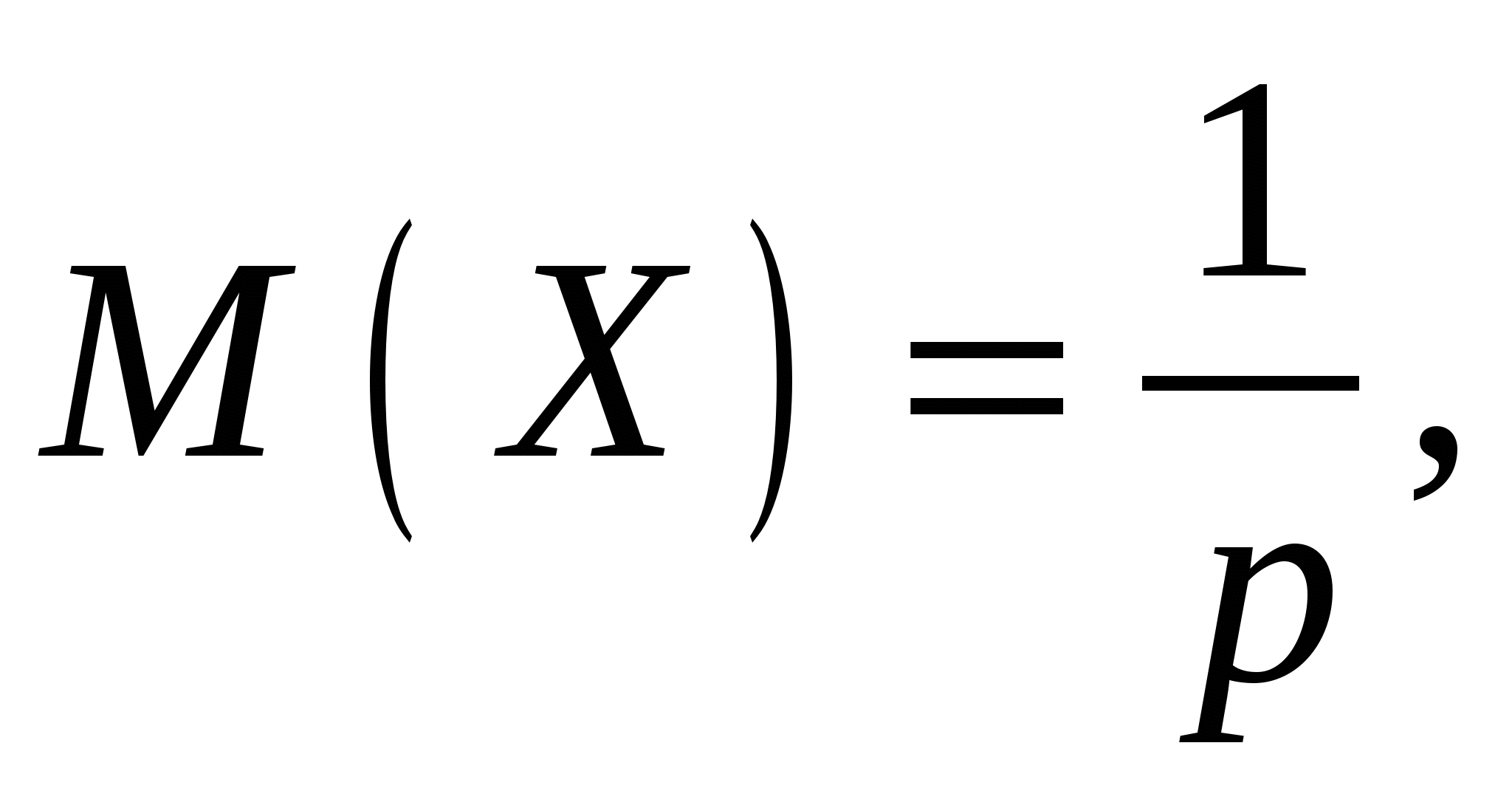 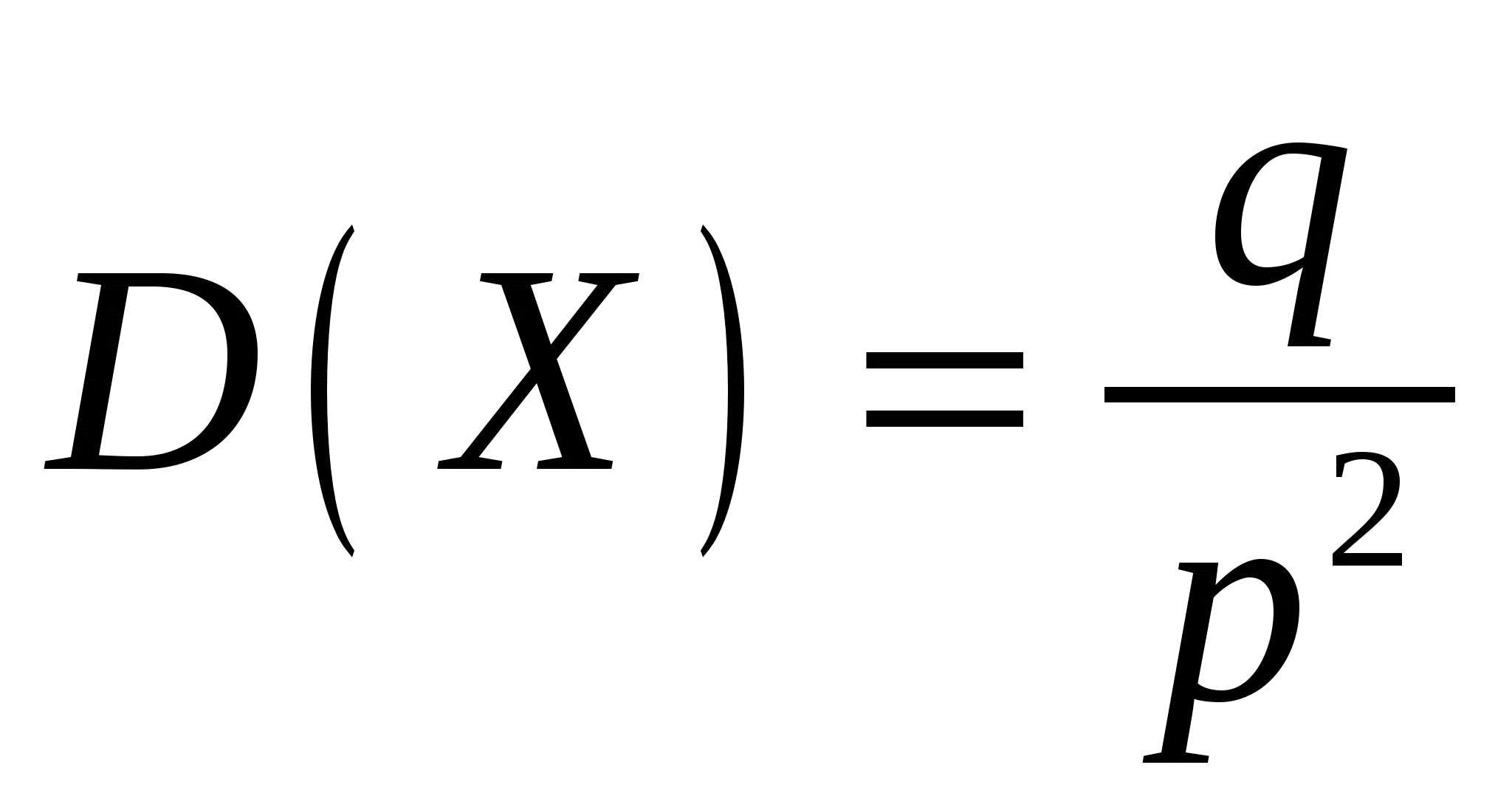 . .Пример 1. Производится ряд попыток включить двигатель. Каждая занимает время Решение. Число попыток
По свойствам математического ожидания и дисперсии 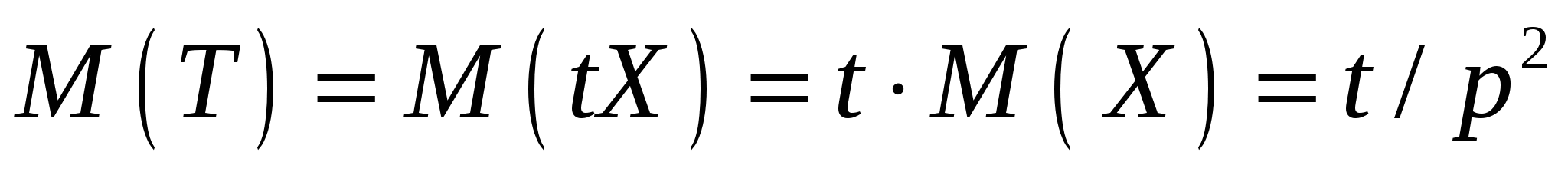 , ,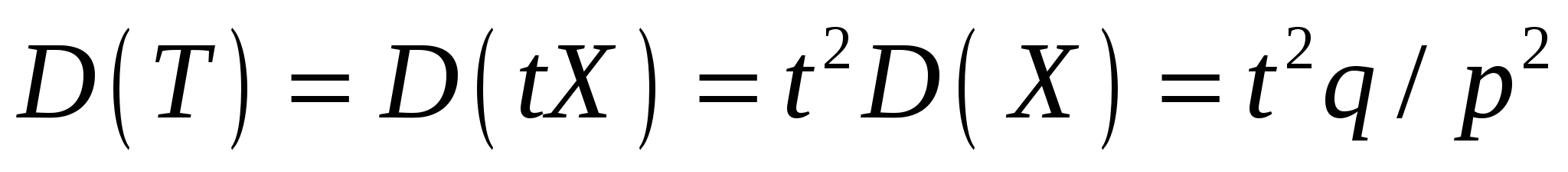 . .Пример 2. Имеется 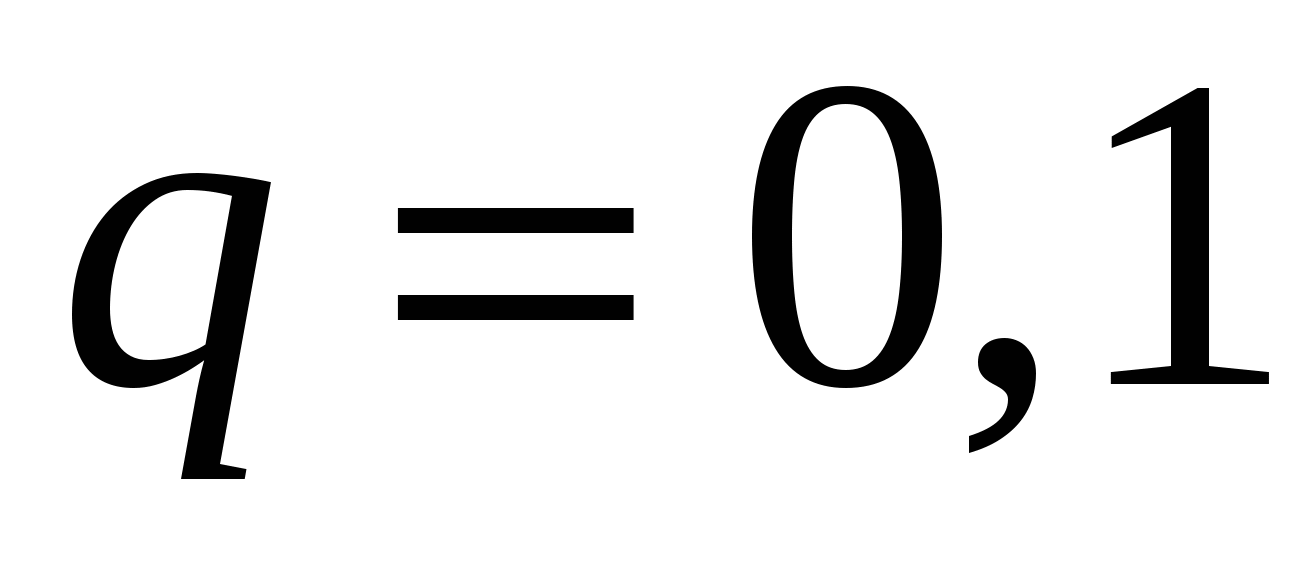 имеет дефект. Лампочка ввинчивается в патрон и включается ток; при этом дефектная лампочка сразу же перегорает и заменяется новой. Построить ряд распределения числа лампочек имеет дефект. Лампочка ввинчивается в патрон и включается ток; при этом дефектная лампочка сразу же перегорает и заменяется новой. Построить ряд распределения числа лампочек Решение. По условию
4. Закон равномерного распределения вероятностей Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом, то есть такими, закон распределения которых имеет некоторую стандартную форму. Были рассмотрены примеры таких законов распределения для дискретных случайных величин (биномиальный и Пуассона). Для непрерывных случайных величин тоже существуют часто встречающиеся виды закона распределения, и в качестве первого из них рассмотрим равномерный закон. Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение (f(x) = const при a ≤ x ≤ b, f(x) = 0 при x < a, x > b. Непрерывная случайная величина Х подчинена закону равномерного распределения вероятностей, если на интервале, которому принадлежат все возможные значения Х , плотность вероятностей постоянна и равна 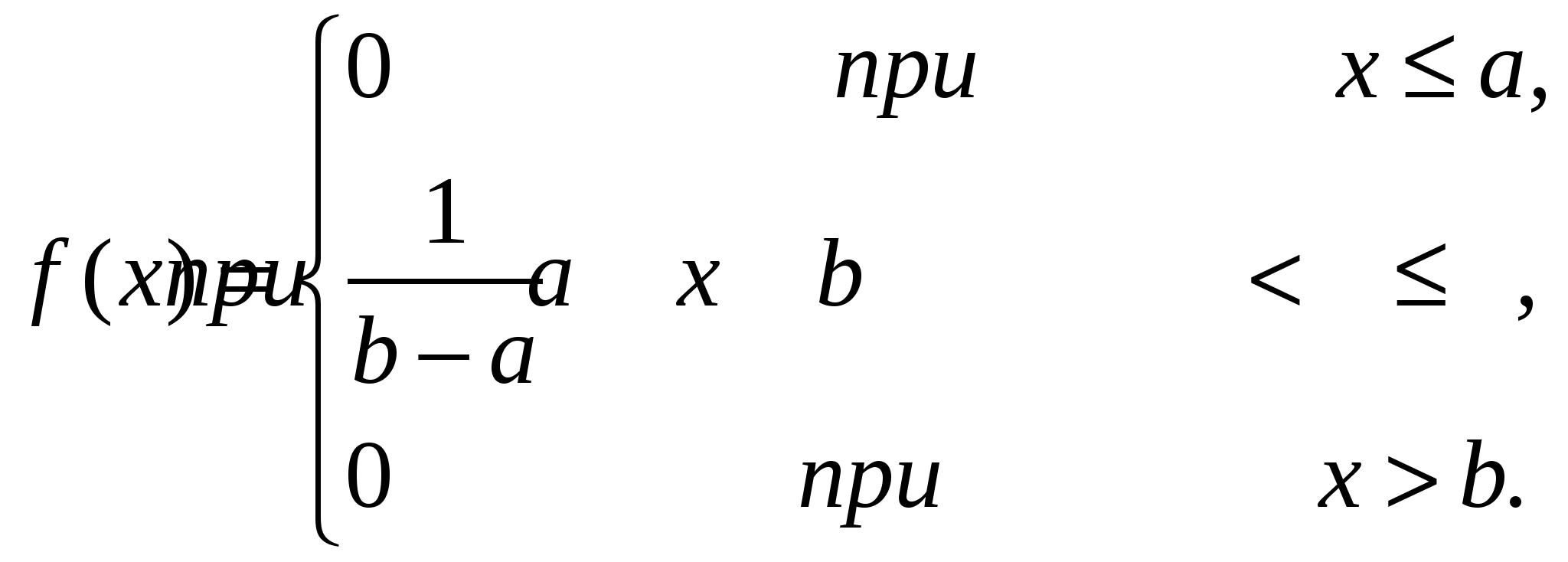 а функции распределения F(x): 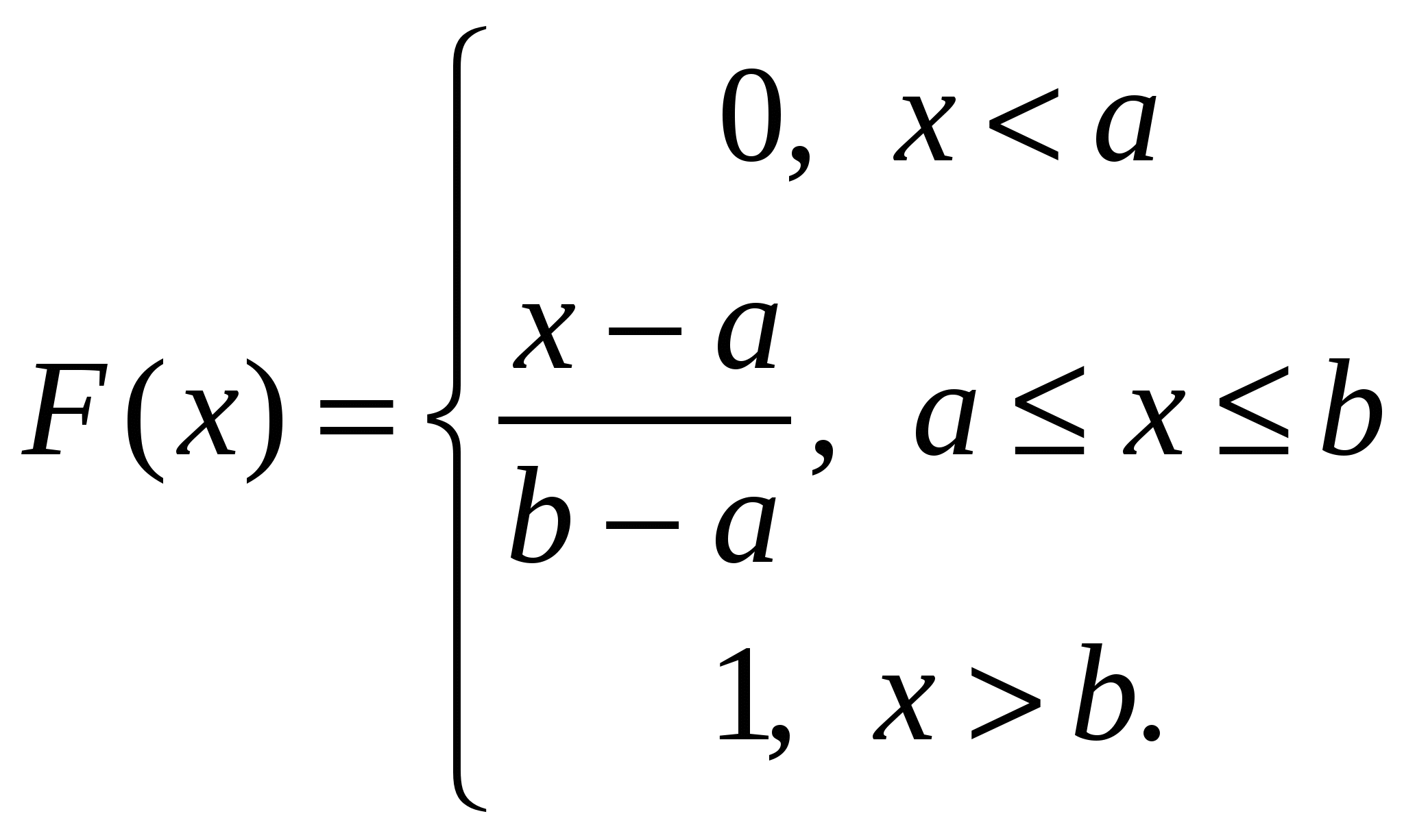 График плотности вероятностей равномерно распределенной случайной величины Х и ее функции распределения F(x) показан на рисунке. 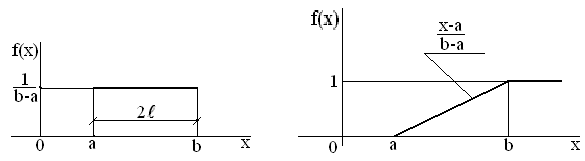 Обычно вместо параметров aи bиспользуют математическое ожидание Х и половину ширины Обычно вместо параметров aи bиспользуют математическое ожидание Х и половину ширины Очевидно, 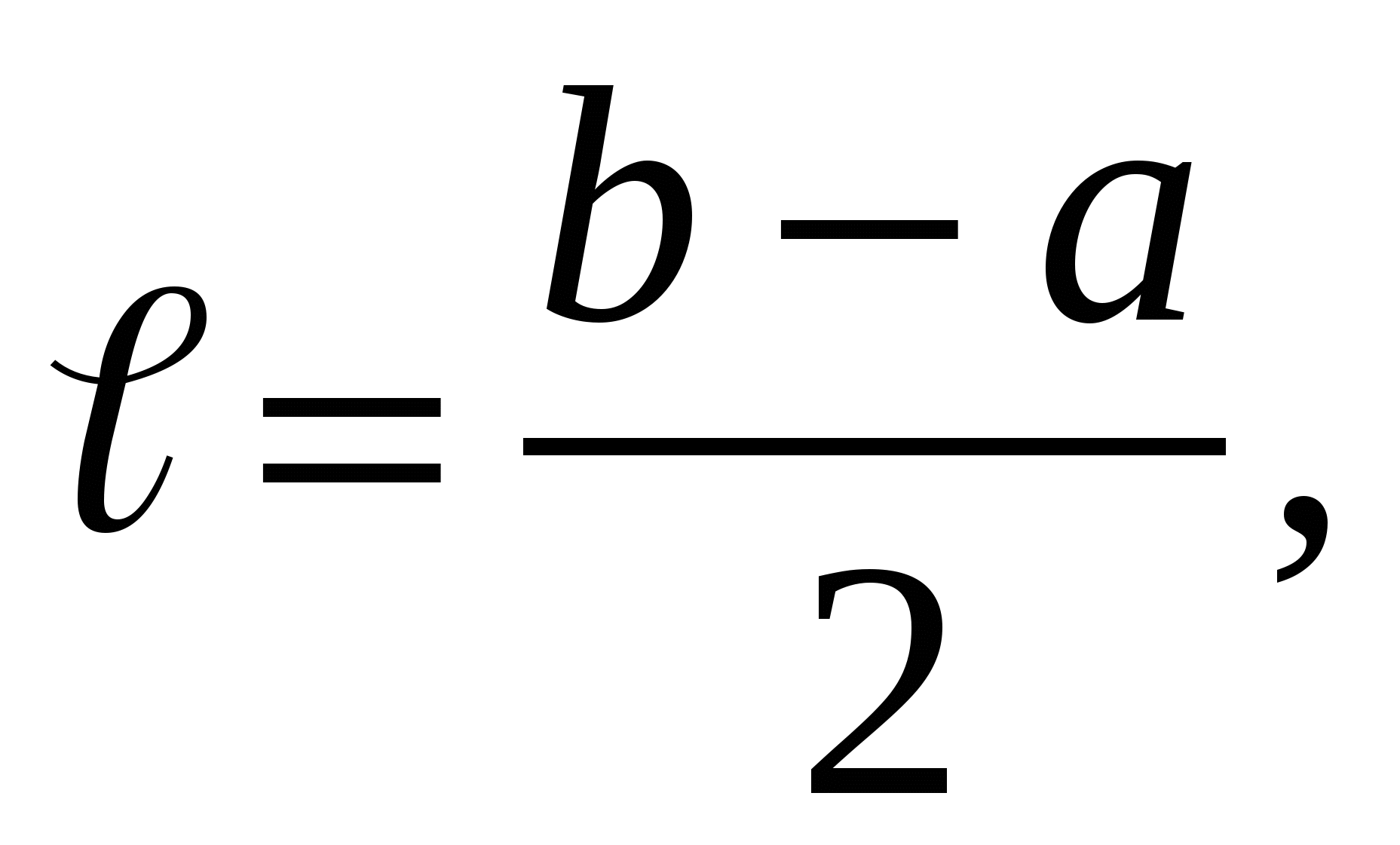 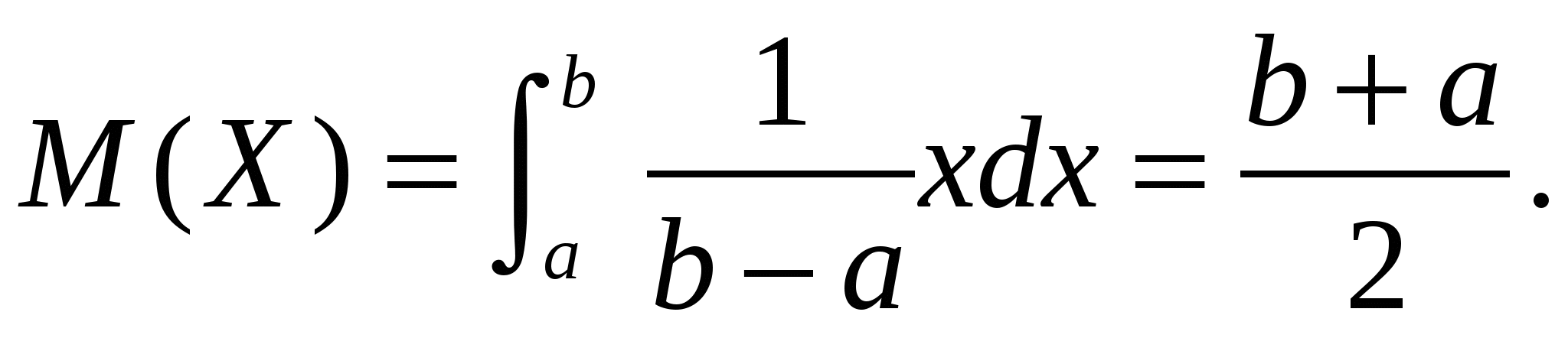 Дисперсия закона равномерного распределения  . .Вероятность попадания равномерно распределенной случайной величины на интервал 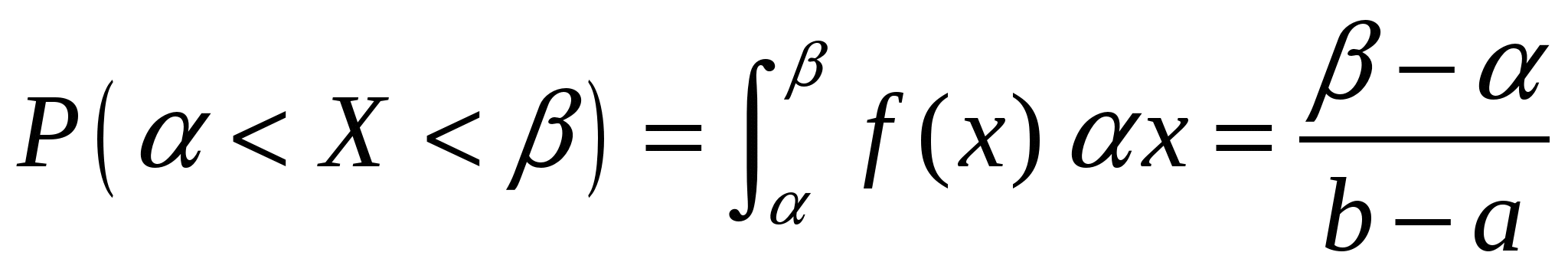 . .Пример. Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут. Решение. Время ожидания является случайной величиной, равномерно распределенной в интервале [0, 5]. Тогда 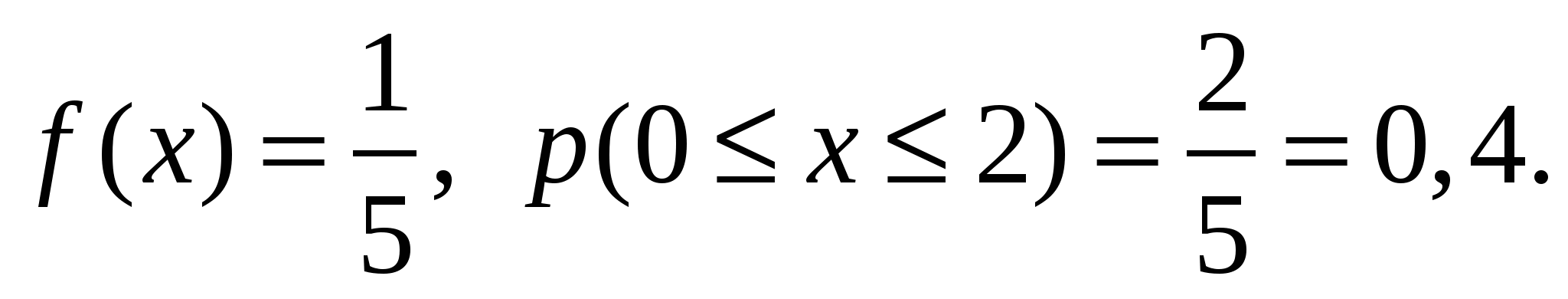 Для равномерно распределенной на отрезке [a, b] непрерывной случайной величины 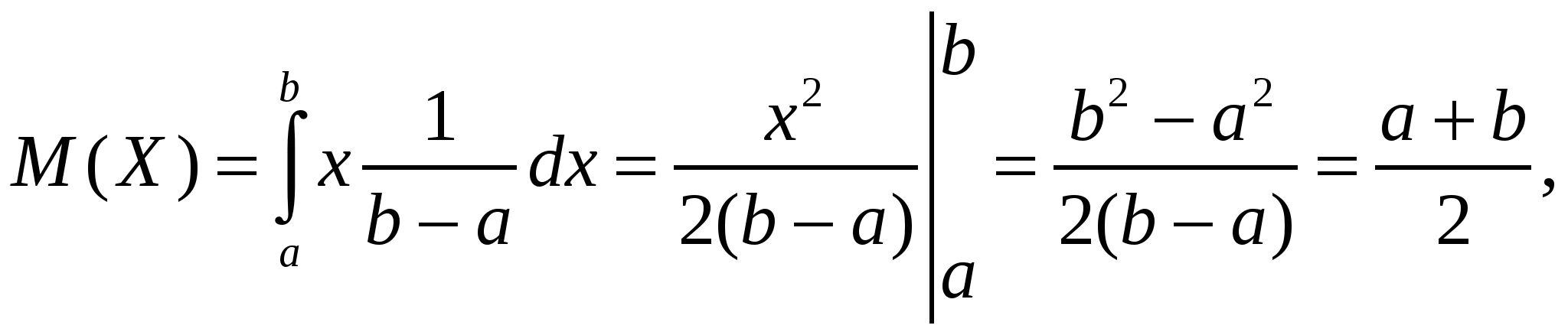 то есть математическое ожидание равномерно распределенной случайной величины равно абсциссе середины отрезка [a, b] . то есть математическое ожидание равномерно распределенной случайной величины равно абсциссе середины отрезка [a, b] .Дисперсия 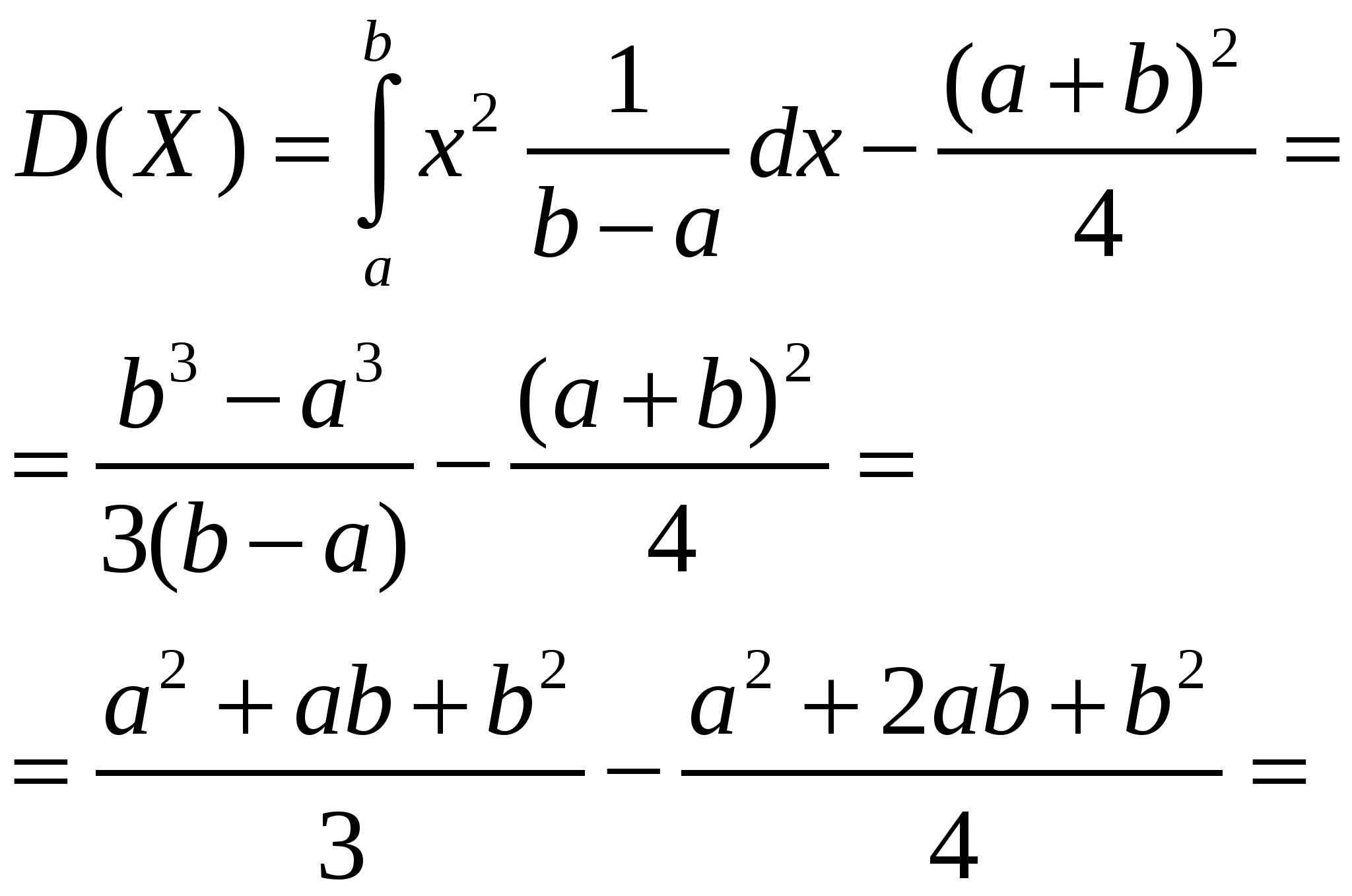 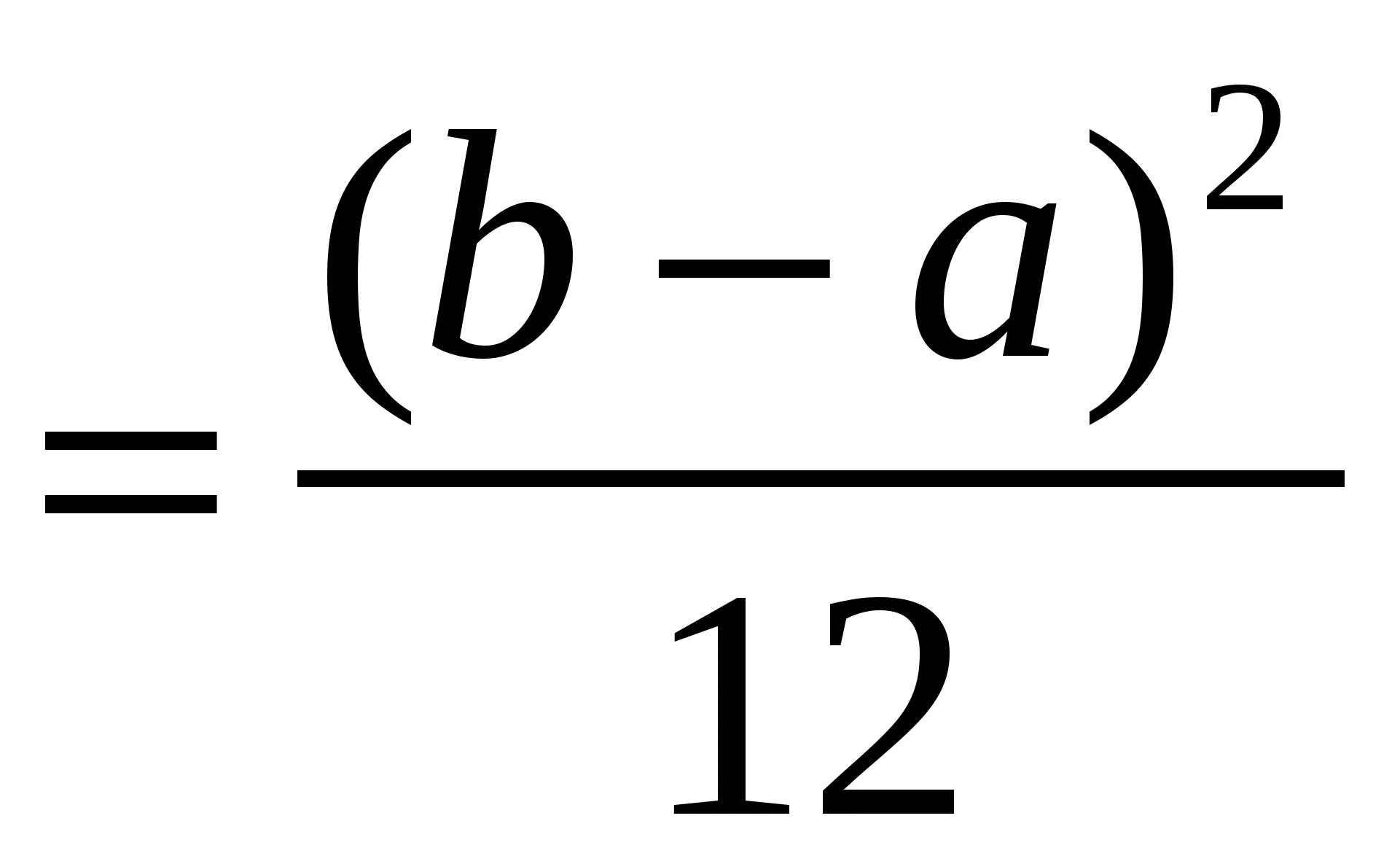 . .5. Показательный (экспоненциальный) закон распределенияПоказательное распределение широко применяется в теории надежности, в теории массового обслуживания. Непрерывная случайная величина подчинена показательному закону распределения, если ее плотность вероятностей равна 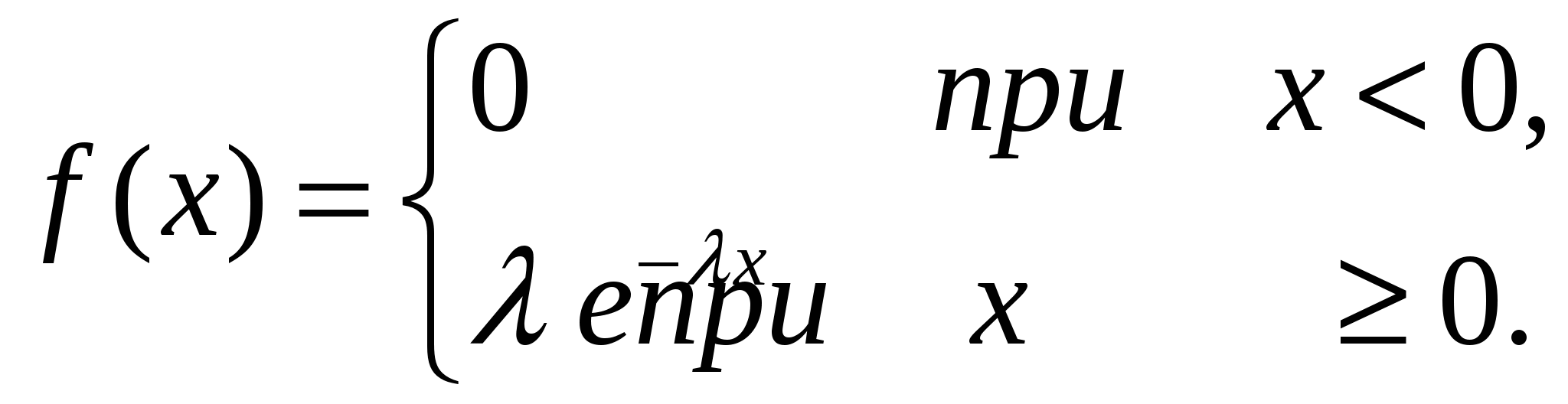 Интегральная функция распределения показательного закона: 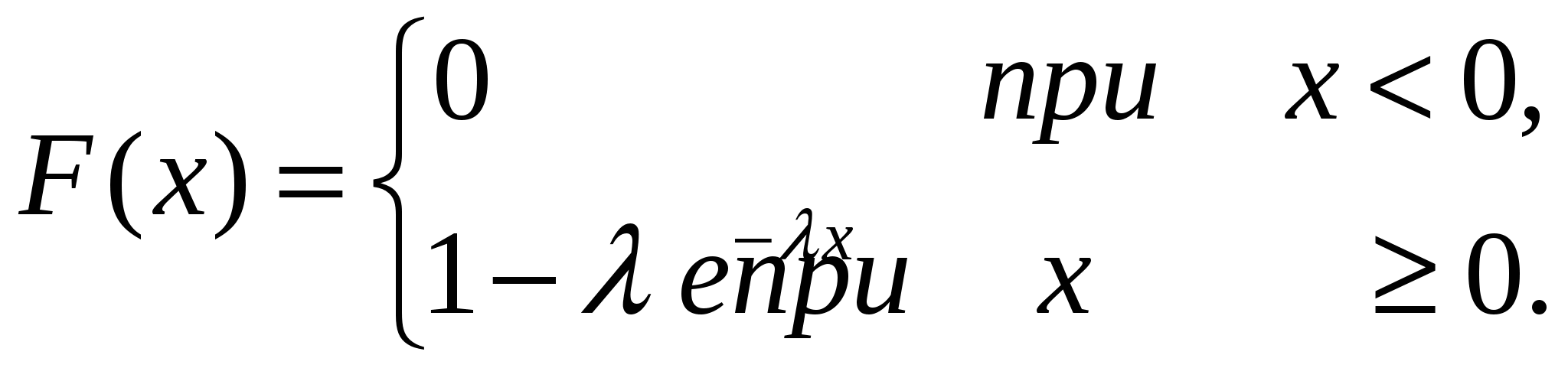 Графики 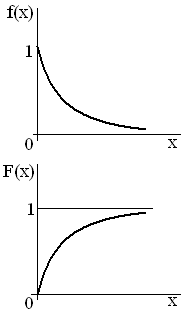 В отличие от нормального распределения, показательный закон определяется только одним параметром λ. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько. Вероятность попадания на конечный интервал 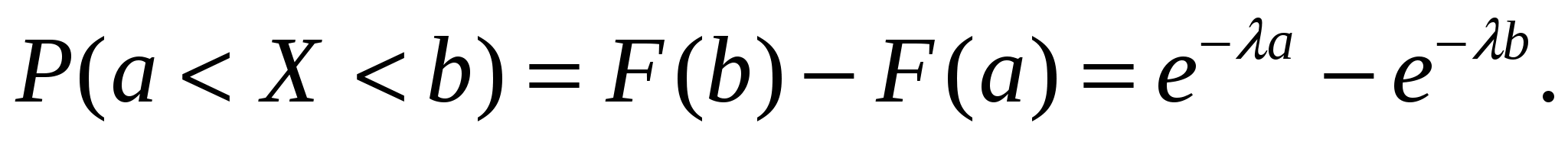 Числовые характеристики показательного распределения 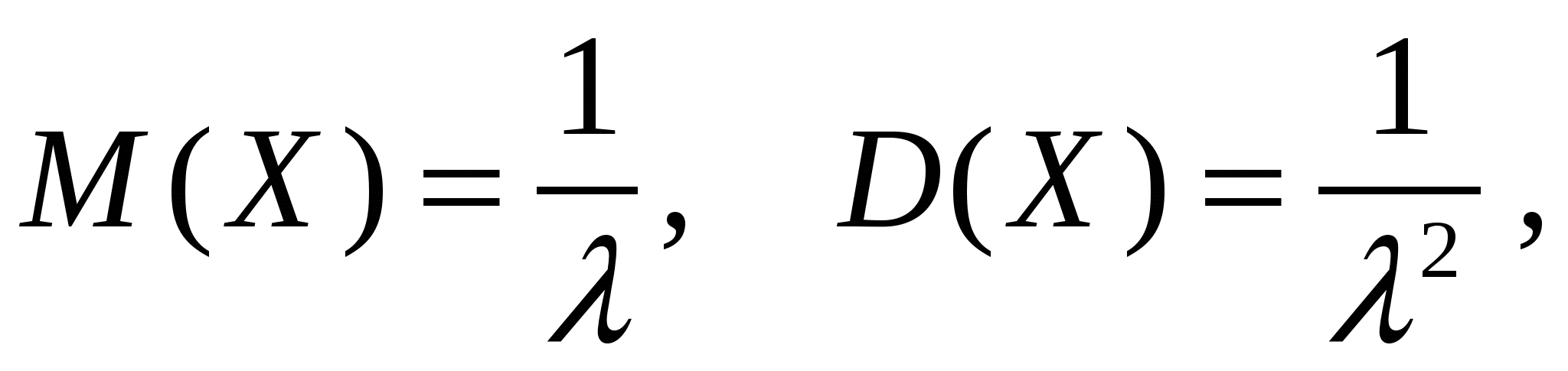 следовательно, следовательно, 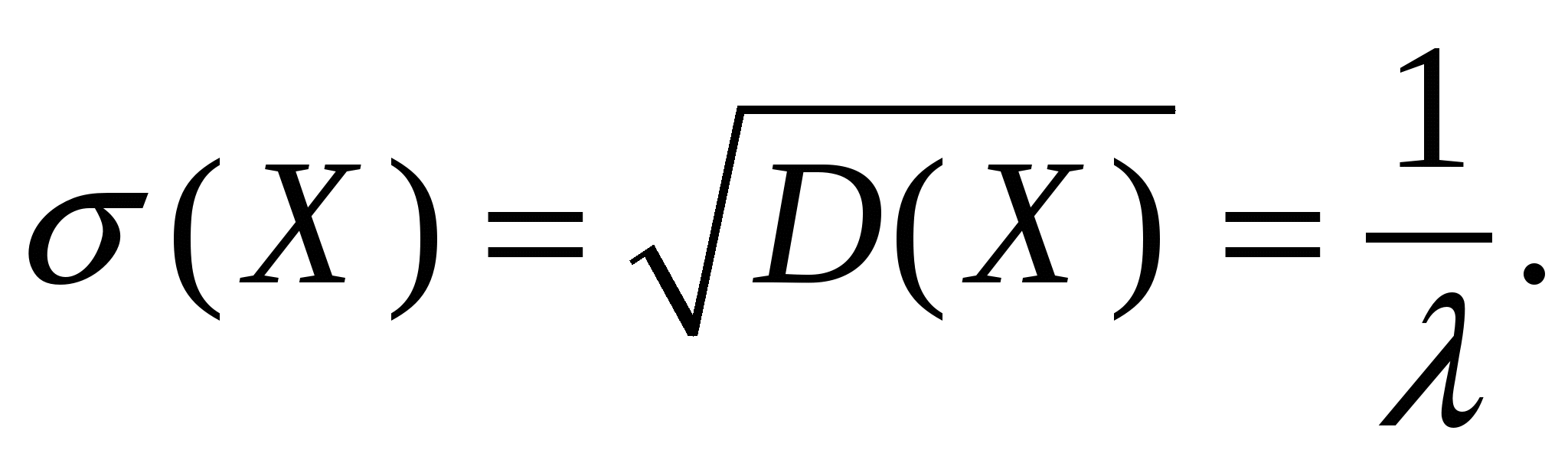 Поэтому математическое ожидание равно среднему квадратическому отклонению. Это равенство является характерным признаком показательного распределения. Пусть Эту функцию называют функцией надежности. Показательный закон надежности. Часто длительность безотказной работы элемента имеет показательное распределение, то есть Следовательно, функция надежности в этом случае имеет вид: 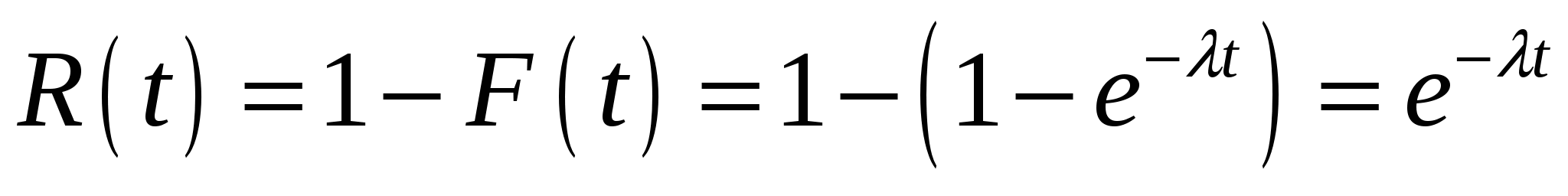 . .Показательным законом надежности называют функцию надежности, определяемую равенством Пример 1. Испытываются два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение Решение. Вероятность отказа первого элемента за 6 часов равна Вероятность отказа второго элемента за то же время Вероятность отказа двух элементов по теореме умножения вероятностей равна Вероятности безотказной работы каждого элемента Поэтому вероятность отказа только одного элемента будет равна Пример 2. Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f(t) = 0,1 e-0,1tприt ≥ 0. Найти вероятность того, что элемент проработает безотказно в течение 10 часов. Решение. Так как λ = 0,1, R(10) = e-0,1·10 = e-1 = 0,368. Задачи для самостоятельной работы 1. Написать плотность и функцию распределения показательного закона, если параметр 2. Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности 3. Найти дисперсию и среднее квадратическое отклонение показательного закона, заданного функцией распределения 4. Обычно совещание длится час. На этот раз за час оно не закончилось. Какова вероятность того, что оно закончится в ближайшие 15 мин. Длительность совещания распределена по показательному закону. 5. Длительность междугородних телефонных разговоров распределена примерно по показательному закону, разговор продолжается в среднем 3 мин. Найти вероятность того, что очередной разговор будет продолжаться более 3 мин. Определить долю разговоров, которые длятся менее 1 мин. Найти вероятность того, что разговор, который длится уже 10 мин, закончится в течение ближайшей минуты, а также математическое ожидание и дисперсию длительности разговора. 6. Устройство, состоящее из 5 независимо работающих элементов, включается на время t. Вероятность отказа каждого из элементов за это время равна 0,2. Найти вероятность того, что за время t откажут: 1) 3 элемента; 2) не менее 4; 3) не более 4 6.6 Нормальный закон распределения Непрерывная случайная величина подчинена нормальному закону распределения (закону распределения Гаусса), если ее плотность вероятностей равна 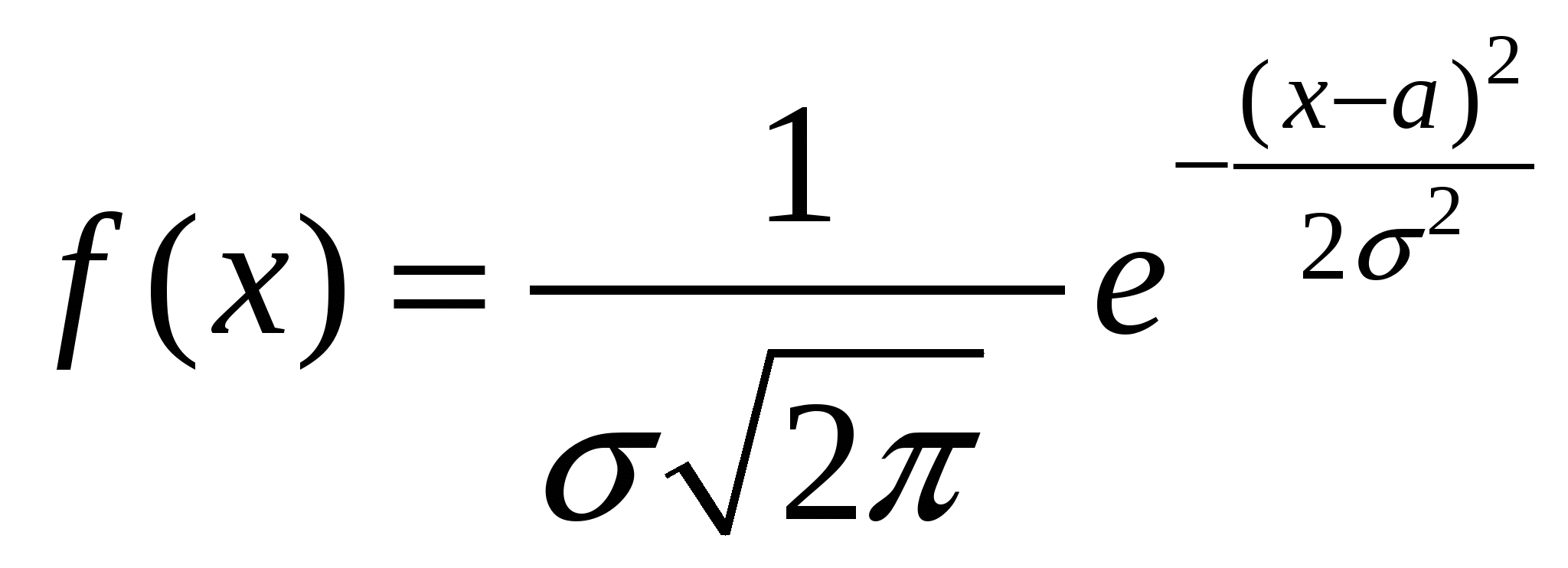 . .Здесь График плотности нормального распределения называют нормальной кривой (кривой Гаусса). График плотности вероятностей нормально распределенной случайной величины (называемый нормальной или гауссовой кривой) показан на рисунке. 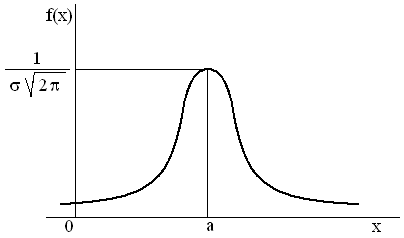
Вероятность попадания нормально распределенной случайной величины на произвольный конечный интервал ( 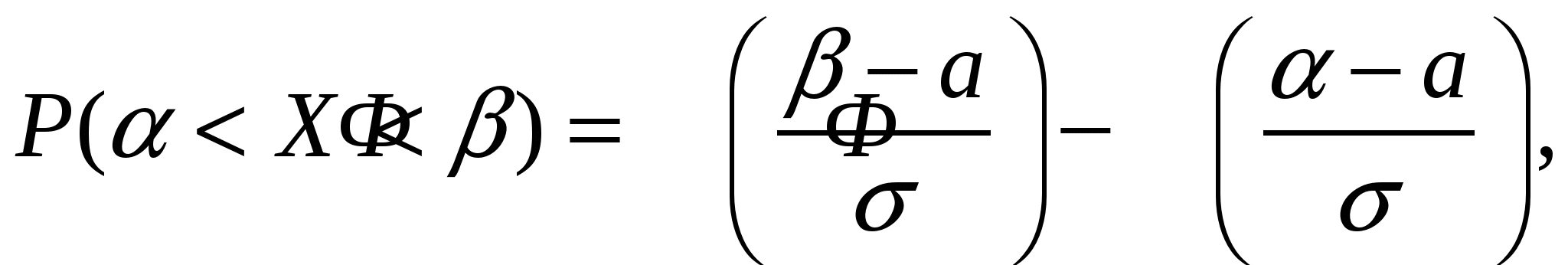 где 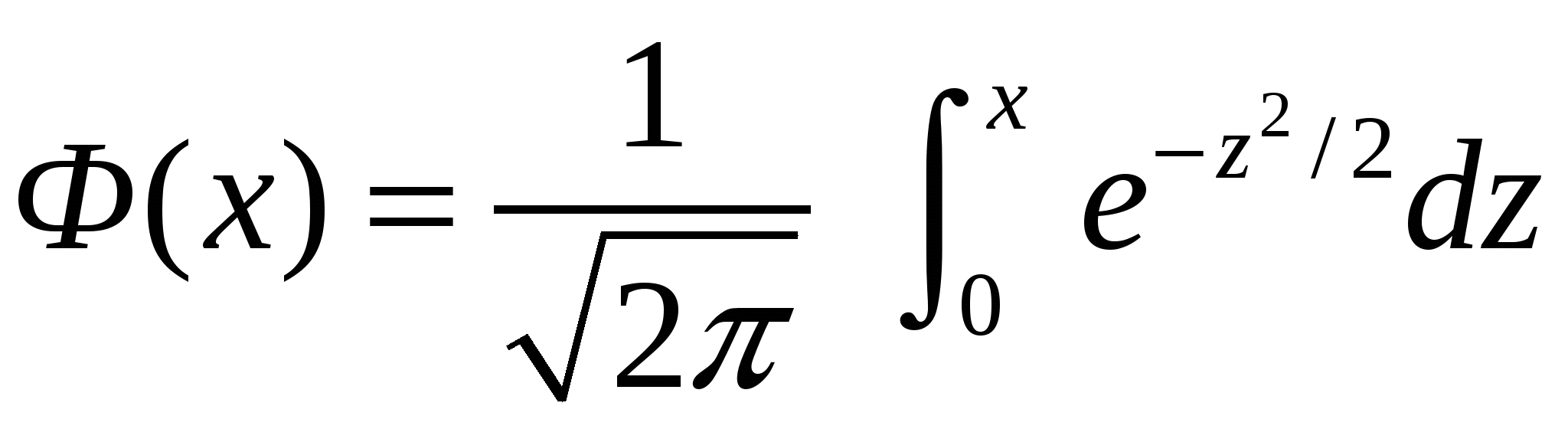 - функция Лапласа. - функция Лапласа.Функция Лапласа табулирована. При пользовании таблицами следует иметь в виду, что она нечетная: Вероятность попадания нормально распределенной случайной величины на интервал, симметричный относительно среднего значения, равна В частности, при На этом и базируется важное для приложений правило трех сигм: Если случайная величина распределена по нормальному закону, то с вероятностью, близкой к достоверности, можно считать, что практически все рассеивание укладывается на интервале Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ. Пример 1. На станке изготовляется партия однотипных деталей. Длина детали X - случайная величина, распределенная по нормальному закону с параметрами 1) вероятность того, что длина наудачу взятой детали заключена между 17,7 см и 18,4 см; 2) какое отклонение длины детали от номинального размера можно гарантировать с вероятностью 0,95? 3) в каких пределах будут заключены практически все длины деталей? Решение. 1). 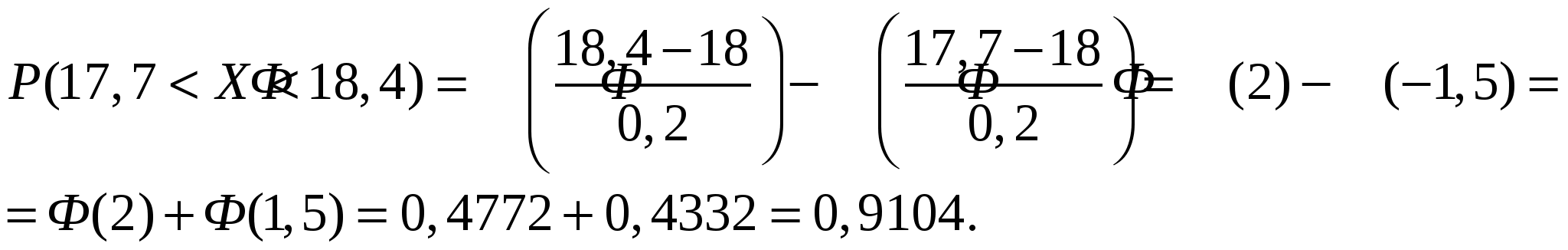 2). Воспользуемся формулой Следовательно, 3). По правилу трех сигм можно считать, что практически все длины деталей с вероятностью 0,9973 будут заключены в интервале Пример 2. Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектной длиной), равным 60 мм. Фактическая длина изготовленных деталей не менее 58 мм и не более 62 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 61 мм; б) меньше 60,5 мм. Решение. Предварительно найдем неизвестный параметр нормального распределения откуда Следовательно, Пример 3. Случайная величина Х имеет нормальное распределение с параметрами а = 3, σ = 2. Найти вероятность того, что она примет значение из интервала (4, 8). Решение. 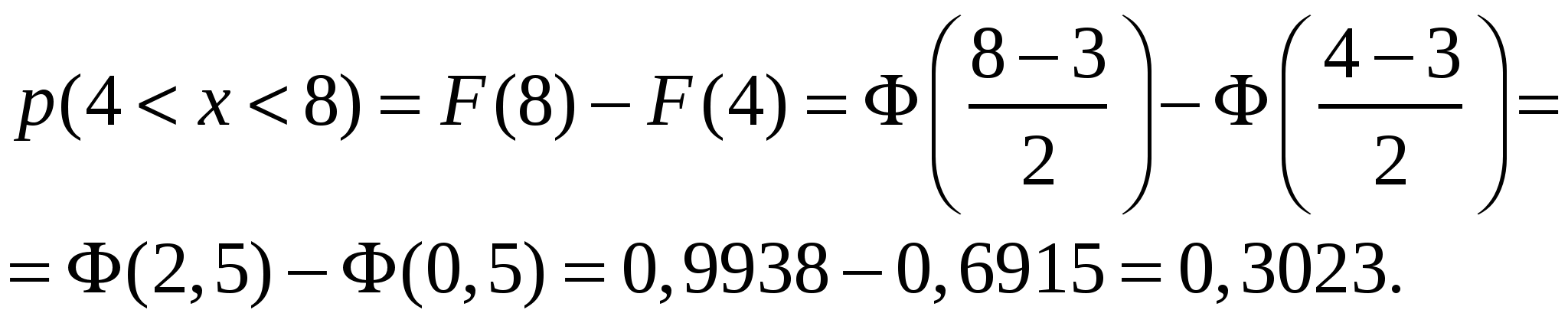 Для вычисления математического ожидания нормально распределенной случайной величины воспользуемся тем, что интеграл Пуассона 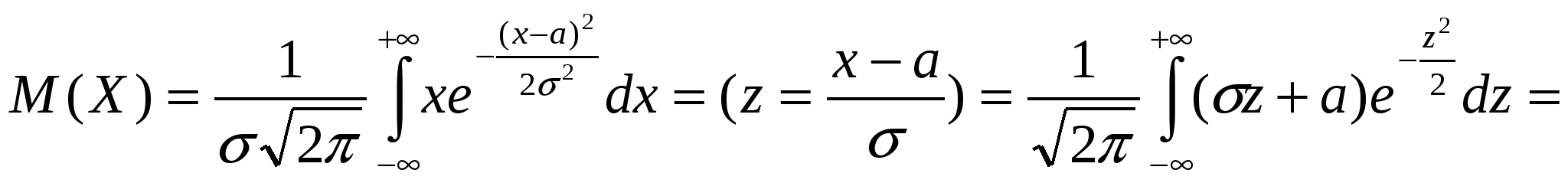 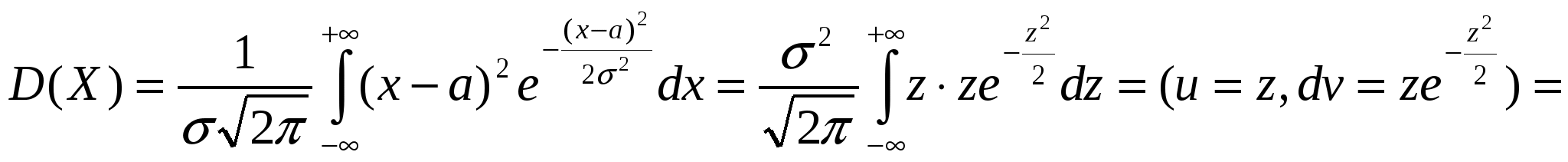 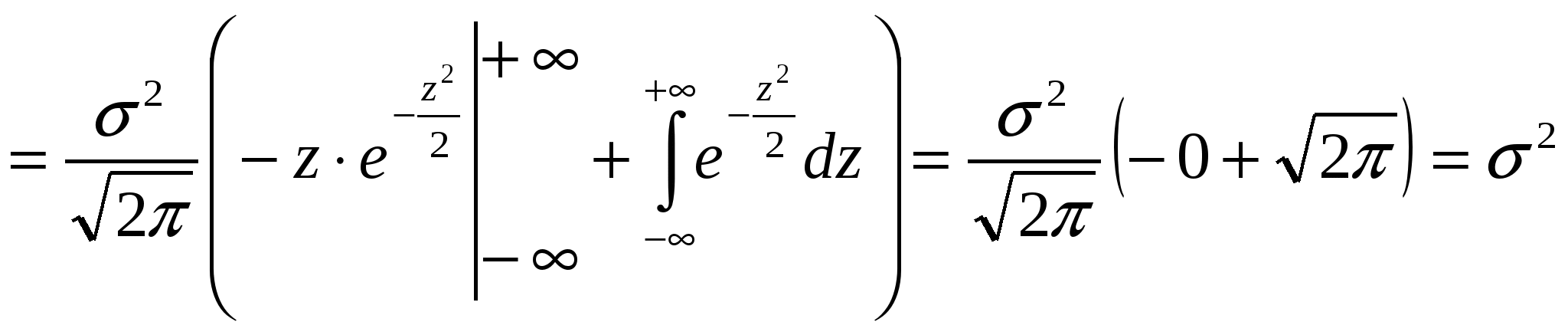 . .Следовательно, параметры нормального распределения (а и σ) равны соответственно математическому ожиданию и среднему квадратическому отклонению исследуемой случайной величины. |

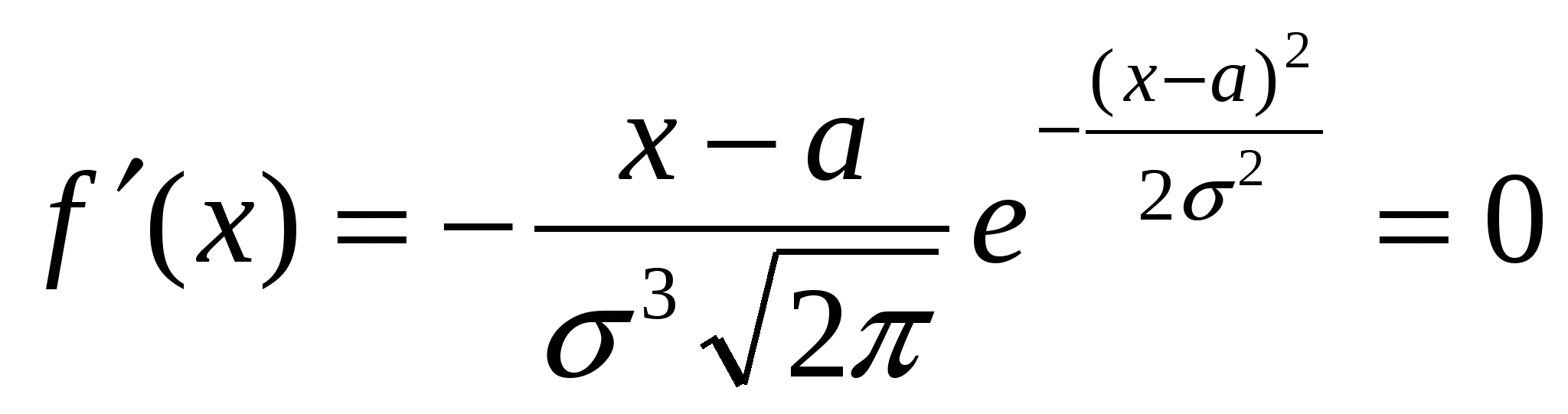 при х = а;
при х = а; 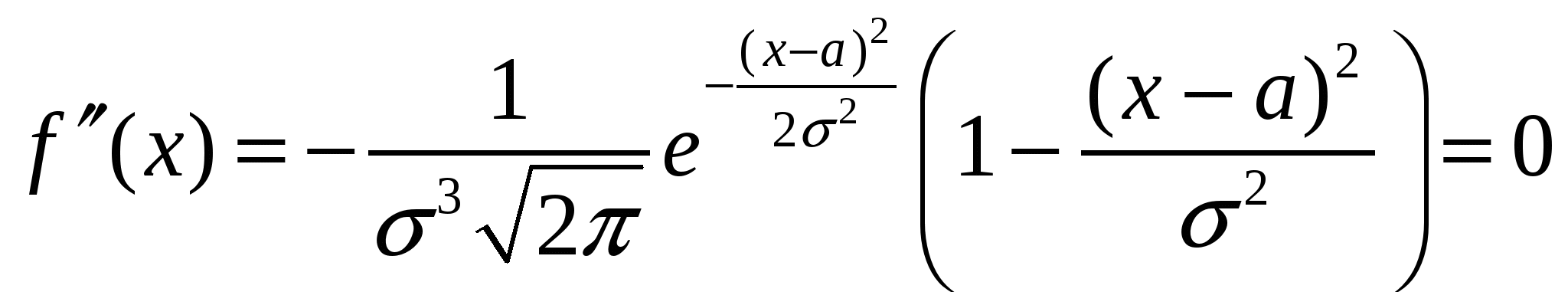 при
при 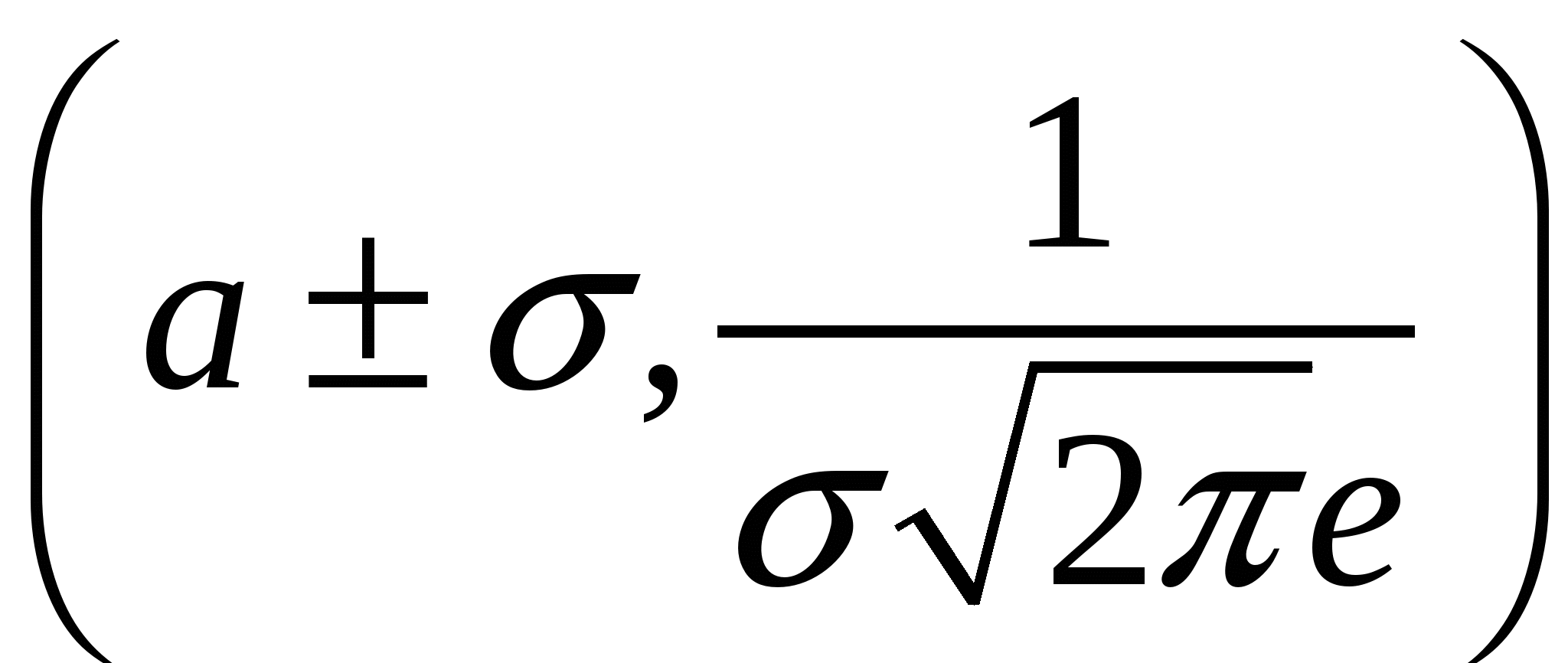 являются точками перегиба.
являются точками перегиба.