ввфф. Случайные величины. Закон ряда распределения список, в котором перечислены значения дсв и вероятности их реализации. Отображается в виде таблицы и график многоугольного распределения
 Скачать 25.77 Kb. Скачать 25.77 Kb.
|
|
Случайные величины – величины, которые в результате испытаний принимают числовое значение, заранее неизвестное и зависящее от случайных причин. Виды случайных величин: Дискретные и Непрерывные. Дискретная случайная величина – величина, которая принимает отдельное и точное значение с определенной вероятностью. (Точные значения, п: оценка на экзамене). Способы задания ДСВ: Закон ряда распределения – список, в котором перечислены значения ДСВ и вероятности их реализации. Отображается в виде таблицы и график многоугольного распределения. Функции распределения – функция, определяющая вероятность того, что СВ (Х) в результате испытания примет значение. (F(X) = D(X < x)) Геометрическое столкновение – вероятность того, что СВ примет значение, которое изображается на числовой оси точкой.  Свойства функции распределения: 0 <= F(x) <= 1 F(x) – неубывающая Если х1 > x2, тогда F(x2) > F(x1) Значение функции F (- 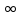 ) = 0, F(+ ) = 0, F(+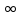 ) = 1 ) = 1[a,b) P (a <=x < b) = F(b) – F(a) Непрерывная случайная величина – величина, значения которой полностью заполняет некоторый промежуток (конечный или бесконечный). (п: 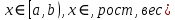 . .Плотностьюраспределениявероятностей НСВ - функция производная от функции распределения: Свойства: 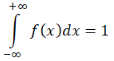 Математическое ожидание – сумма произведений всех ее возможных значений на их вероятность. 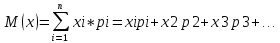 Величина x – мат. Ожидание (х) называется отклонением СВ (х) от мат.ожидания. Свойства М(Х): М(С) = С, где С – константа. М(С*Х) = С* М(Х). М (Х +- У +- Z) = M(X) +- M(Y) +- M(Z) (с умножением также) M (x – M(X)) = 0. Дисперсия (рассеяние ДСВ) – математическое ожидание квадрата отклонения СВ от математического ожидания. 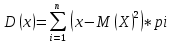 или или 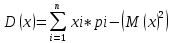 Свойства дисперсии: D(C) = 0 D(C *X) = 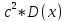 D (X +- Y +- Z) = D(X) +- D(Y) +- D(Z) D (X * Y) = 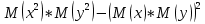 Среднеквадратичное отклонение – значение квадратного корня из дисперсии случайной величины. 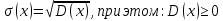 Свойства: 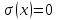 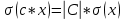 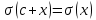 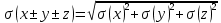 Мода – случайная величина с наибольшей вероятностью. |
