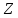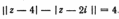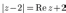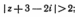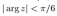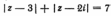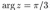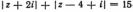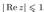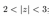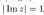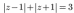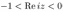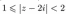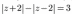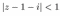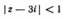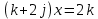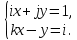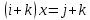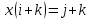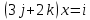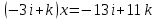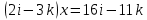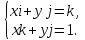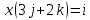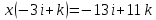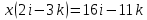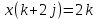|
Индивидуальные задания. индивидуальные задания ЧС озо. Закон сложения (1) m4 a5, b2 4 Свойство умножения 2р m6 a3, b2
Вариант
|
1. Доказать утверждения о натуральных числах (нумерация из файла лекции), опираясь на аксиомы и доказанное ранее
|
2.Доказать, что группу (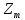 ,+) нельзя линейно упорядочить ,+) нельзя линейно упорядочить
|
3.Доказать, что уравнение 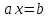 неразрешимо в неразрешимо в 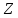
|
1
|
Теорема 2.2,
|
m=5
|
a=3, b=1
|
2
|
Свойство сложения 2S
|
m=3
|
a=4, b=1
|
3
|
Закон сложения (1)
|
m=4
|
a=5, b=2
|
4
|
Свойство умножения 2р
|
m=6
|
a=3, b=2
|
5
|
Свойство порядка П2
|
m=5
|
a=4, b=3
|
6
|
Свойство сложения 3S
|
m=3
|
a=3, b=1
|
7
|
Закон сложения (2)
|
m=4
|
a=4, b=1
|
8
|
Свойство умножения 3р
|
m=6
|
a=5, b=2
|
9
|
Свойство порядка П3
|
m=5
|
a=3, b=2
|
10
|
Закон умножения (2)
|
m=3
|
a=4, b=3
|
4.
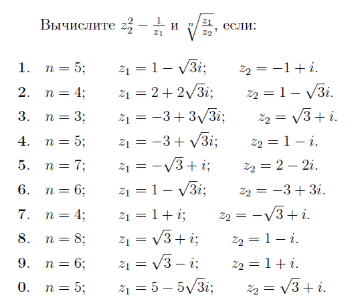
5. Изобразить в плоскости и описать словами множество точек плоскости, соответствующих комплексным числам z, удовлетворяющим условиям
вариант
|
|
|
1
|
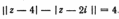
|
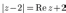
|
2
|
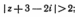
|
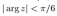
|
3
|
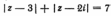
|
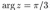
|
4
|
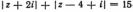
|
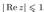
|
5
|
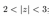
|
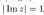
|
6
|
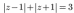
|
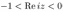
|
7
|
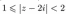
|
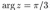
|
8
|
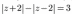
|
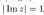
|
9
|
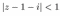
|
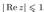
|
10
|
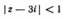
|
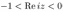
|
6.
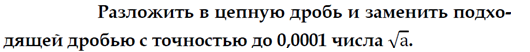

7. Записать следующие действительные числа, заданные в десятичной системе счисления, в q-ой системе
варианты
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
q
|
3
|
5
|
7
|
3
|
5
|
7
|
3
|
5
|
7
|
3
|
a
|
13,65
|
13,65
|
12,36
|
23,65
|
23,65
|
32,36
|
53,65
|
53,65
|
52,36
|
43,65
|
8. Решить в 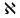 , (сделать проверку!!, помним про отсутствие коммутативности умножения в алгебре кватернионов): , (сделать проверку!!, помним про отсутствие коммутативности умножения в алгебре кватернионов):
вариант
|
уравнение
|
систему
|
1
|
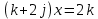
|
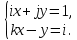
|
2
|
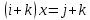
|
3
|
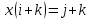
|
4
|
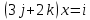
|
5
|
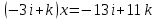
|
6
|
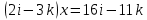
|
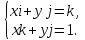
|
7
|
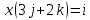
|
8
|
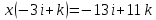
|
9
|
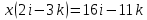
|
10
|
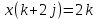
| |
|
|
 Скачать 230.85 Kb.
Скачать 230.85 Kb.

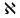 , (сделать проверку!!, помним про отсутствие коммутативности умножения в алгебре кватернионов):
, (сделать проверку!!, помним про отсутствие коммутативности умножения в алгебре кватернионов):
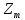 ,+)
,+) 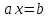 неразрешимо в
неразрешимо в