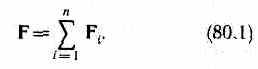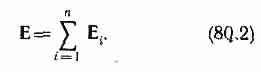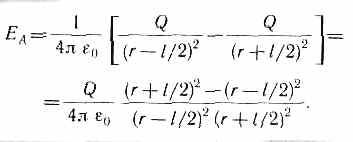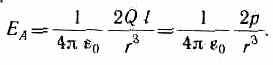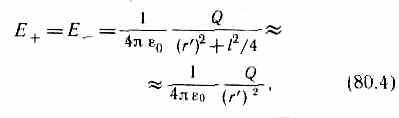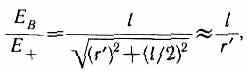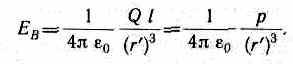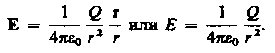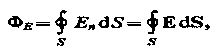1. Электрический заряд и его свойства.
Модель точечного заряда и модели с непрерывным распределением заряда.
Закон сохранения электрического заряда.
- Электрический заряд q – это физическая величина, которая характеризует свойство тел или частиц вступать в электромагнитные взаимодействия и определяет значения сил и энергий при таких взаимодействиях. Ему присущи следующие фундаментальные свойства:
1) электрический заряд существует в двух видах: отрицательные и положительные заряды;
2) Электрический заряд дискретен; (ДИСКРЕТНОСТЬ — противоположность непрерывности)
3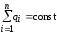
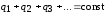
) алгебраическая сумма электрических зарядов замкнутой системы остается постоянной (закон сохранения электрического заряда);
или ,
4) электрический заряд - величина релятивистки инвариантная, т.е. не зависит от системы отсчета, а значит, не зависит от того, движется заряд или покоится.
- Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
Распределение заряда в пространстве может быть дискретным и непрерывным.
При дискретном распределении заряд сконцентрирован в математической точке пространства.
При непрерывном распределении различают линейное, поверхностное и объемное распределение заряда.
при непрерывном распределении заряда вдоль линии вводится понятие линейной плотности зарядов τ
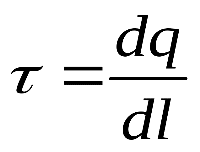
где dq – заряд малого участка линии длиной dl.
при непрерывном распределении заряда по некоторой поверхности вводится понятие поверхностной плотности зарядов σ
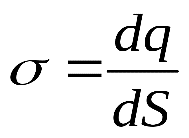
где dq – заряд малого участка поверхности площадью dS.
при непрерывном распределении заряда в каком-либо объеме вводится понятие объемной плотности зарядов ρ
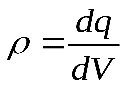
- Закон сохранения электрического заряда утверждает: электрические заряды не возникают и не исчезают, они могут быть лишь переданы от одного тела другому или перемещены внутри данного тела. Это фундаментальный закон природы, экспериментально подтвержденный в 1843 году английским физиком М. Фарадеем:
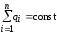
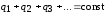 или , или ,
т.е. алгебраическая сумма зарядов замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается постоянной.
СУММАРНЫЙ ЗАРЯД ВСЕХ ЭЛЕМЕНТОВ, ОБРАЗУЮЩИХ ИЗОЛИРОВАННУЮ СИСТЕМУ ОСТАЁТСЯ НЕИЗМЕННЫМ ПРИ ЛЮБЫХ ПРОЦЕССАХ В ЭТОЙ СИСТЕМЕ
2. Закон Кулона.
Напряженность электрического поля.
Принцип суперпозиции электростатических полей.
- Основной закон взаимодействия электрических зарядов был найден Шарлем Кулоном в 1785 г. экспериментально. Кулон установил, что сила взаимодействия 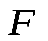 между двумя небольшими заряженными металлическими шариками обратно пропорциональна квадрату расстояния между двумя небольшими заряженными металлическими шариками обратно пропорциональна квадрату расстояния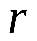 между ними и зависит от величины зарядов между ними и зависит от величины зарядов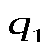 и и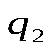 : :
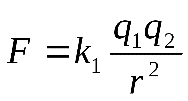 , ,
где 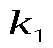 -коэффициент пропорциональности -коэффициент пропорциональности 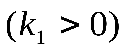 . .
Силы, действующие на заряды, являются центральными, то есть они направлены вдоль прямой, соединяющей заряды. 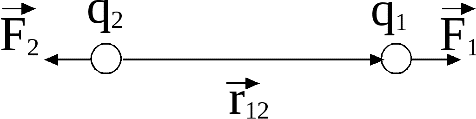
Закон Кулона можно записать в векторной форме: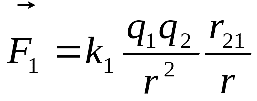 , ,
где 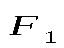 -вектор силы, действующей на заряд -вектор силы, действующей на заряд 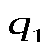 со стороны заряда со стороны заряда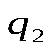 , ,
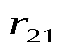 - радиус-вектор, соединяющий заряд - радиус-вектор, соединяющий заряд 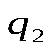 с зарядом с зарядом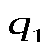 ; ;
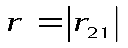 - модуль радиус-вектора. - модуль радиус-вектора.
Сила, действующая на заряд 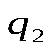 со стороны со стороны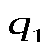 равна равна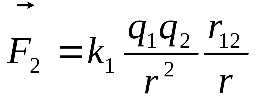 , ,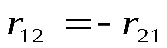 . .
Закон Кулона в такой форме
справедлив только для взаимодействия точечных электрических зарядов, то есть таких заряженных тел, линейными размерами которых можно пренебречь по сравнению с расстоянием между ними.
выражает силу взаимодействия между неподвижными электрическими зарядами, то есть это электростатический закон.
Формулировка закона Кулона:
Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними.
Коэффициент пропорциональности 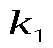 в законе Кулоназависит в законе Кулоназависит
от свойств среды
выбора единиц измерения величин, входящих в формулу.
Поэтому 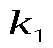 можно представить отношением можно представить отношением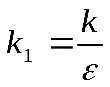 , ,
где 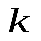 -коэффициент, зависящий только от выбора системы единиц измерения; -коэффициент, зависящий только от выбора системы единиц измерения;
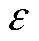 - безразмерная величина, характеризующая электрические свойства среды, называется относительной диэлектрической проницаемостью среды. Она не зависит от выбора системы единиц измерения и равна единице в вакууме. - безразмерная величина, характеризующая электрические свойства среды, называется относительной диэлектрической проницаемостью среды. Она не зависит от выбора системы единиц измерения и равна единице в вакууме.
Тогда закон Кулона примет вид: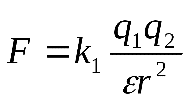 , ,
для вакуума 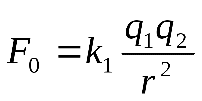 , ,
тогда 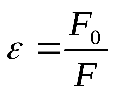 -относительная диэлектрическая проницаемость среды показывает, во сколько раз в данной среде сила взаимодействия между двумя точечными электрическими зарядами -относительная диэлектрическая проницаемость среды показывает, во сколько раз в данной среде сила взаимодействия между двумя точечными электрическими зарядами 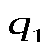 и и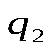 , находящимися друг от друга на расстоянии , находящимися друг от друга на расстоянии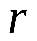 , меньше, чем в вакууме. , меньше, чем в вакууме.
В системе СИ коэффициент 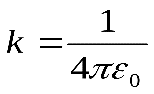 , и , и
закон Кулона имеет вид: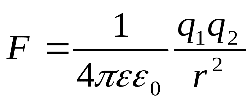 . .
Это рационализированная запись закона Кулона.
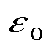 - электрическая постоянная, - электрическая постоянная, 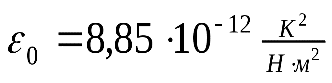 . .
В векторной форме закон Кулона принимает вид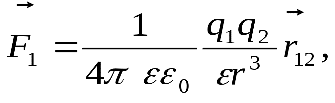
где 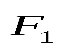 -вектор силы, действующей на заряд -вектор силы, действующей на заряд 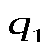 со стороны заряда со стороны заряда 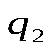 , ,
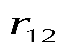 - -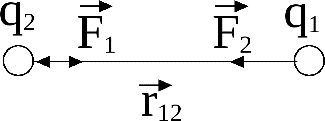 радиус-вектор, соединяющий заряд радиус-вектор, соединяющий заряд 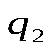 с зарядом с зарядом 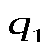
(рис. 1.2),
r –модуль радиус-вектора 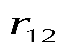 . .
Всякое заряженное тело состоит из множества точечных электрических зарядов, поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равна векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.
- Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами.
На всякий другой заряд, внесенный в это пространство, действуют электростатические силы Кулона.
Если в каждой точке пространства действует сила, то говорят, что в этом пространстве существует силовое поле.
Поле наряду с веществом является формой материи.
Если поле стационарно, то есть не меняется во времени, и создается неподвижными электрическими зарядами, то такое поле называется электростатическим.
Электростатика изучает только электростатические поля и взаимодействия неподвижных зарядов.
Для характеристики электрического поля вводят понятие напряженности.
Напряженностью в каждой точке электрического поля называется вектор 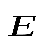 , численно равный отношению силы, с которой это поле действует на пробный положительный заряд, помещенный в данную точку, и величины этого заряда, и направленный в сторону действия силы. , численно равный отношению силы, с которой это поле действует на пробный положительный заряд, помещенный в данную точку, и величины этого заряда, и направленный в сторону действия силы.
Пробный заряд, который вносится в поле, предполагается точечным и часто называется пробным зарядом.
- Он не участвует в создании поля, которое с его помощью измеряется.
- предполагается, что этот заряд не искажает исследуемого поля, то есть он достаточно мал и не вызывает перераспределения зарядов, создающих поле.
Если на пробный точечный заряд 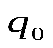 поле действует силой поле действует силой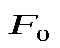 , то напряженность , то напряженность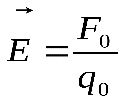 . .
Единицы напряженности:
СИ: 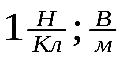
В системе СИ выражение для 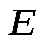 поля точечного заряда: поля точечного заряда:
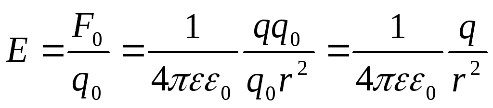 . .
В векторной форме: 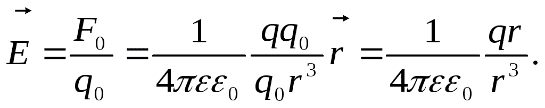
Здесь 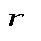 – радиус-вектор, проведенный из зарядаq , создающего поле, в данную точку. – радиус-вектор, проведенный из зарядаq , создающего поле, в данную точку.
Та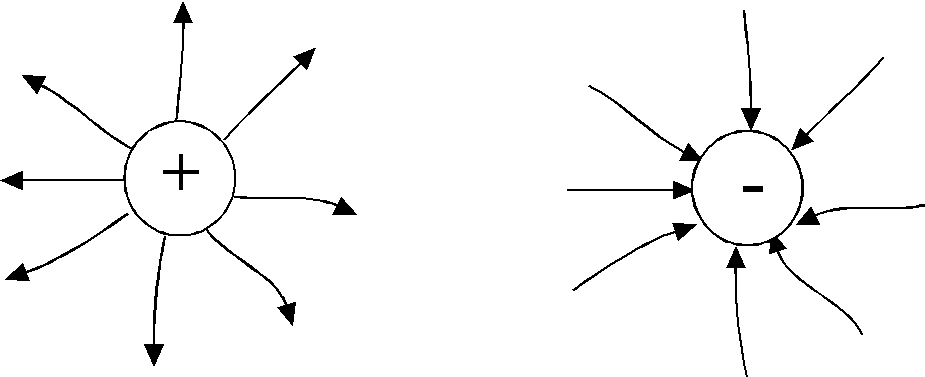 ким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3) ким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)
- от заряда, если он положительный, «исток»
- и к заряду, если он отрицательный «сток»
Для графической интерпретации электрического поля вводят понятие силовой линии или линии напряженности. Это
кривая, касательная в каждой точке к которой совпадает с вектором напряженности.
Линия напряженности начинается на положительном заряде и заканчивается на отрицательном.
Линии напряженности не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление.
- Рассмотрим метод определения значения и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов q1, q2, ..., Qn.
Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил , т.е. результирующая сила F, действующая со стороны поля на пробный заряд Q0, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Qi:
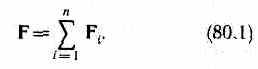
Согласно (79.1), F=Q0E и Fi,=Q0Ei, где Е—напряженность результирующего поля, а Еi — напряженность поля, создаваемого зарядом Qi. Подставляя последние выражения в (80.1), получим
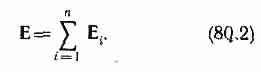
Формула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов ( + Q, -Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор

совпадающий по направлению с плечом диполя и равный произведению заряда
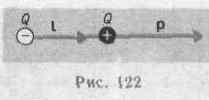
|Q| на плечо l, называется электрическим моментом диполя р или дипольным моментом (рис. 122).
Согласно принципу суперпозиции (80.2), напряженность Е поля диполя в произвольной точке
Е=Е+ + Е-,
где Е+ и Е- — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля на продолжении оси диполя и на перпендикуляре к середине его оси.
1. Напряженность поля на продолжении оси диполя в точке А (рис. 123). Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна
ЕA=Е+-Е-.
Обозначив расстояние от точки А до середины оси диполя через л, на основании формулы (79.2) для вакуума можно записать
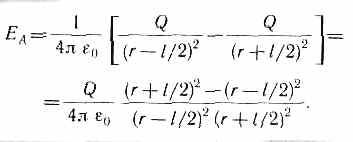
Согласно определению диполя, l/2<
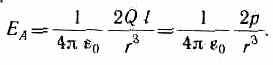
2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В (рис. 123). Точка В равноудалена от зарядов, поэтому
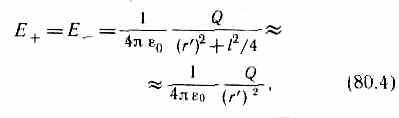
г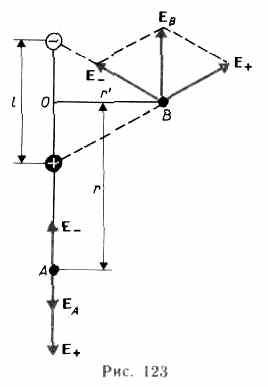
де r'— расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся плечо диполя и вектор ев, получим
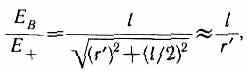
133
откуда
ЕB=Е+l/r'. (80.5)
Подставив в выражение (80.5) значение (80.4), получим
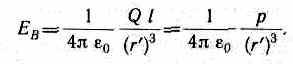
+Вектор ЕB имеет направление, противоположное электрическому моменту диполя (вектор р направлен от отрицательного заряда к положительному).
3. Напряженность поля точечного заряда в вакууме.
Примеры графического изображения электростатических полей.
- Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Электростатическое поле- это поле которое создается неподвижными электрическими зарядами. Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Напряженность электростатического поля(Н/Кл) в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля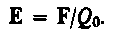
напряженность поля точечного заряда в вакууме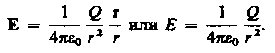
Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду Графически электростатическое поле изображают с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности — радиальные прямые, выходящие из заряда, если он положителен , и входящие в него, если заряд отрицателен . Величина называется потоком вектора напряженности (Вм) через площадку dS.
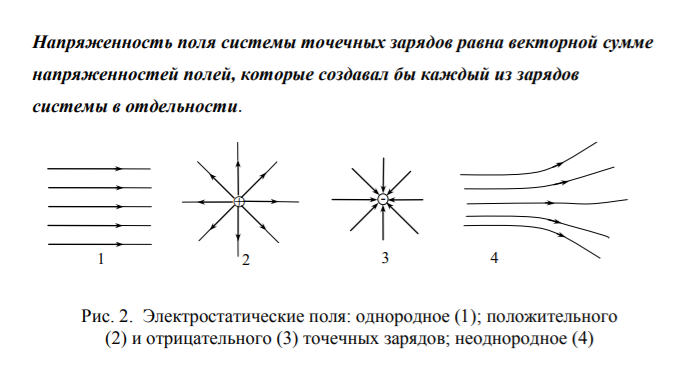
 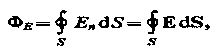
- Изображение электростатического поля с помощью векторов напряженности 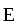 в различных точках поля является очень неудобным, так как картина получается весьма запутанной. Фарадей предложил более простой и наглядный метод изображения электростатического поля с помощьюлиний напряженностей или силовых линий. Силовыми линиями называются кривые, касательные к которым в каждой точке совпадают с направлением вектора напряженности поля (рис.1.2). Направление силовой линии совпадает с направлением в различных точках поля является очень неудобным, так как картина получается весьма запутанной. Фарадей предложил более простой и наглядный метод изображения электростатического поля с помощьюлиний напряженностей или силовых линий. Силовыми линиями называются кривые, касательные к которым в каждой точке совпадают с направлением вектора напряженности поля (рис.1.2). Направление силовой линии совпадает с направлением 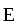 . Силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных. Силовые линии не пересекаются, так как в каждой точке поля вектор . Силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных. Силовые линии не пересекаются, так как в каждой точке поля вектор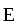 имеет лишь одно направление. Электростатическое поле считается однородным, если напряженность во всех его точках одинакова по величине и направлению. Силовыми линиями такого поля являются прямые, параллельные вектору напряженности. имеет лишь одно направление. Электростатическое поле считается однородным, если напряженность во всех его точках одинакова по величине и направлению. Силовыми линиями такого поля являются прямые, параллельные вектору напряженности.
Силовые линии поля точечных зарядов - радиальные прямые, выходящие из заряда и уходящие в бесконечность, если он положителен (рис.1.3а). Если заряд отрицателен, направление силовых линий оказывается обратным: они начинаются в бесконечности и оканчиваются на заряде -q (рис.1.3б). Поле точечных зарядов обладает центральной симметрией.
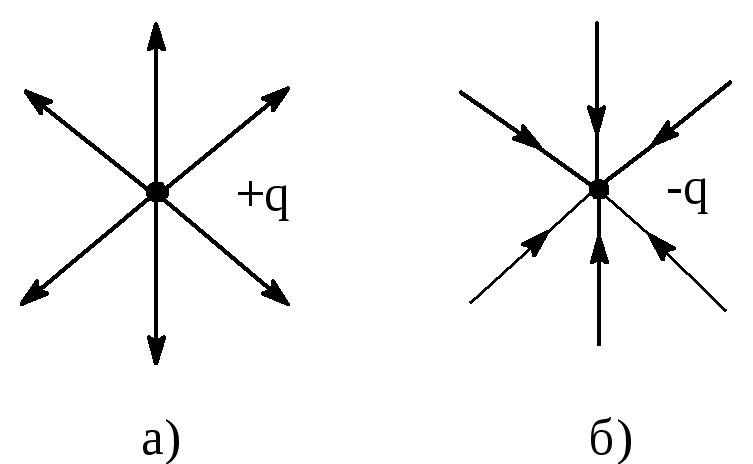
Рис.1.3. Линии напряженности точечных зарядов: а - положительного, б - отрицательного.
На рис.1.3 изображены плоские сечения электростатических полей системы двух одинаковых по величине зарядов: а) заряды, одинаковые по знаку, б) заряды, разные по знаку.
4. Электрический диполь.
Поле диполя.
Дипо́ль— идеализированная система, служащая для приближённого описания поля, создаваемого, вообще говоря, более сложными системами зарядов, а также для приближенного описания действия внешнего поля на такие системы.Дипольное приближение, выполнение которого обычно подразумевается, когда говорится ополе диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка
Типичный пример диполя — два заряда, равных по величине и противоположных по знаку, находящихся друг от друга на расстоянии, очень малом по сравнению с расстоянием до точки наблюдения. Поле такой системы полностью описывается дипольным приближением.
Электрическое поле диполя
Рассмотрим поле простейшей системы точечных зарядов. Простейшей системой точечных зарядов является электрический диполь. Электрическим диполем называется совокупность равных по величине, но противоположных по знаку двух точечных зарядов –q и +q, сдвинутых друг относительно друга на некоторое расстояние. Пусть 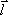 – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор
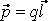
называется электрическим моментом диполя или дипольным моментом, а вектор 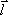 – плечом диполя. Если длина – плечом диполя. Если длина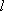 пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным. пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным.
Вычислим электрическое поле электрического точечного диполя. Поскольку диполь точечный, то безразлично в пределах точности расчета от какой точки диполя отсчитывается расстояние r до точки наблюдения. Пусть точка наблюдения А лежит на продолжении оси диполя (рис. 1.13). В соответствии с принципом суперпозиции для вектора напряженности, напряженность электрического поля в этой точке будет равна
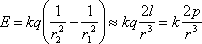 , ,
5. Поток вектора напряженности электростатического поля.
Теорема Гаусса.
6.Поле равномерно заряженной бесконечной плоскости (применение теоремы Гаусса)
7. Поле двух бесконечных параллельных разноимённо заряженных плоскостей. 8. Поле равномерно заряженной сферической поверхности. 9. Поле объёмно заряженного шара. 10. Поле равномерно заряженного бесконечного цилиндра 11. Работа в поле электростатических сил.
Теорема о циркуляции вектора напряжённости. 12. Потенциал электростатического поля.
Взаимосвязь вектора напряжённости и потенциала. 13. Потенциал поля точечного заряда.
Разность потенциалов.
Эквипотенциальные поверхности. 14. Диэлектрики.
Напряжённость поля в диэлектрике.
Проводники.
Поле внутри проводника. 15. Постоянный электрический ток.
Сила тока.
Плотность тока.
ЭДС источника тока. 16. Закон Ома в интегральной и дифференциальной формах.
Обобщённый закон Ома. 17. Закон Джоуля-Ленца в интегральной и дифференциальной формах. 18. Магнитное поле и его свойства.
Магнитная индукция.
Линии магнитной индукции. 19. Закон Био-Савара-Лапласа.
Его применение.
Принцип суперпозиции магнитных полей. 20. Закон Ампера.
Рамка с током в магнитном поле.
Взаимодействие параллельных токов. 21. Магнитное поле движущегося заряда.
Сила Лоренца. 22. Поток вектора магнитной индукции.
Закон полного тока (теорема о циркуляции вектора В) 23. Явление электромагнитной индукции.
Закон Фарадея.
Правило Ленца. 24. Вихревое электрическое поле.
Циркуляция вектора напряженности электрического поля. 25. Ток смещения.
Плотность тока смещения 26. Уравнения Максвелла (в интегральной форме).
Электромагнитные волны.
27. Абсолютно чёрное тело.
Модель чёрного тела.
Законы теплового излучения.
28. Квантовая гипотеза Планка.
Фотоны.
Энергия, импульс фотона. 29. Фотоэффект: виды и законы.
Уравнение Эйнштейна для фотоэффекта.
Красная граница фотоэффекта. 30. Эффект Комптона.
Комптоновский сдвиг. 31. Корпускулярно-волновой дуализм.
Волны де Бройля.
Соотношение неопределенностей. 32. Модели атома.
Модели атома Томсона и Резерфорда.
Недостатки модели. 33. Атом водорода по Бору.
Постулаты Бора.
Спектр атома водорода по Бору 34. Радиоактивность.
Закон радиоактивного распада.
Виды радиоактивного распада. |
 Скачать 249.58 Kb.
Скачать 249.58 Kb.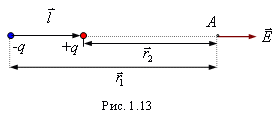
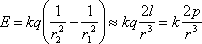 ,
,
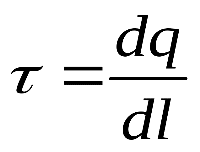
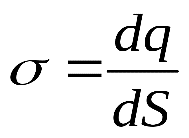

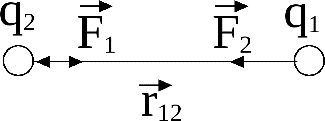 радиус-вектор, соединяющий заряд
радиус-вектор, соединяющий заряд  ким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)
ким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)