Удар шаров. Закон сохранения импульса и закон сохранения механической энергии энергия
 Скачать 116.24 Kb. Скачать 116.24 Kb.
|
   Удар шаров Удар шаровЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА И ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Энергия – это универсальная мера различных форм движения и взаимодействия материи. С различными формами движения материи связывают различные виды энергии: механическую, тепловую, электромагнитную, ядерную и другие. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Работа силы – это количественная характеристика процесса обмена энергией между взаимодействующими телами. При прямолинейном движении тела под действием постоянной силы, которая составляет некоторый угол с направлением перемещения, работа равна: 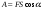 Если сила изменяется как по модулю, так и по направлению, то на бесконечно малом перемещении Если сила изменяется как по модулю, так и по направлению, то на бесконечно малом перемещении  вводится понятие элементарной работы вводится понятие элементарной работы 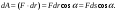 Тогда работа силы на участке траектории от точки 1 до точки 2 равна: Тогда работа силы на участке траектории от точки 1 до точки 2 равна: 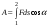 . .Консервативной (потенциальной) называют силу, работа которой определяется только начальным и конечным положениями тела и не зависит от формы пути (силы тяготения, упругости, все центральные силы). Неконсервативными (непотенциальными, диссипативными) являются силы трения и все силы сопротивления. Единица измерения энергии, работы – джоуль (Дж). Кинетическая энергия – это энергия механического движения системы. Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении: 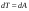 . Используя это равенство, можно получить формулу кинетической энергии . Используя это равенство, можно получить формулу кинетической энергии 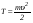 . .Различают пять видов движения тела: поступательное, вращение вокруг неподвижной оси, плоское движение, сферическое движение (движение вокруг неподвижной точки), свободное движение. Первые два вида движений (поступательное и вращение вокруг неподвижной оси) являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из главных или к их совокупности. Поступательное движение – это движение твердого тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению (например, вагон, движущийся по прямому участку пути, кабина колеса обозрения и др.). Вращательное движение вокруг неподвижной оси АВ – это такое движение твердого тела, при котором все точки прямой АВ, жестко связанные с телом, остаются неподвижными. Прямая называется осью вращения тела. Плоское движение – это такое движение, при котором каждая точка твердого тела движется в плоскости, параллельной некоторой неподвижной (в данной системе отсчета) плоскости. Кинетическая энергия вращательного движения определяется по формуле 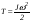 . При сложном движении, когда тело участвует и в поступательном, и во вращательном движении, кинетическая энергия будет складываться из энергии поступательного и энергии вращательного движения . При сложном движении, когда тело участвует и в поступательном, и во вращательном движении, кинетическая энергия будет складываться из энергии поступательного и энергии вращательного движения 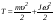 . .Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Работа потенциальных сил равна убыли потенциальной энергии: 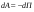 . Используя это соотношение, можно установить связь между потенциальной энергией и потенциальной силой . Используя это соотношение, можно установить связь между потенциальной энергией и потенциальной силой 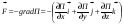 . Вид функции зависит от характера силового поля. Например, потенциальная энергия тела в однородном поле тяжести Земли определяется формулой . Вид функции зависит от характера силового поля. Например, потенциальная энергия тела в однородном поле тяжести Земли определяется формулой 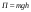 , упругодеформированного тела – , упругодеформированного тела – 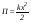 . .Полная механическая энергия системы равна сумме кинетической и потенциальной энергий 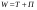 . .Закон сохранения механической энергии: в замкнутой системе тел, между которыми действуют только потенциальные силы, полная механическая энергия остается постоянной 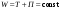 . .Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Скорость изменения импульса материальной точки равна действующей на нее силе 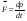 . Векторная величина . Векторная величина 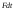 называется элементарным импульсом силы. Согласно второму закону Ньютона изменение импульса материальной точки равно импульсу действующей на нее силы: называется элементарным импульсом силы. Согласно второму закону Ньютона изменение импульса материальной точки равно импульсу действующей на нее силы: 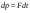 или после интегрирования или после интегрирования 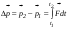 . Среднее значение действующей силы равно . Среднее значение действующей силы равно 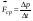 , где , где 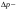 изменение импульса, изменение импульса, 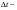 время действия силы. время действия силы.Закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени. Замкнутой называется система, на которую не действуют внешние силы. Этот закон является следствием второго закона Ньютона для системы материальных точек: 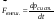 , где , где 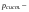 суммарный импульс системы. Если суммарный импульс системы. Если 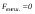 , то , то 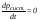 и и 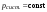 . .Удар – совокупность явлений, связанных со значительными изменениями скорости тела за малый промежуток времени (тысячные доли секунды). Центральный удар – удар, при котором тела до удара движутся по прямой, проходящей через их центры масс. Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Выполняются законы сохранения импульса и механической энергии. Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело. Выполняется закон сохранения импульса и не выполняется закон сохранения механической энергии: вследствие деформации часть кинетической энергии переходит во внутреннюю энергию тел. Упругий удар занимает промежуточное положение между абсолютно упругим и абсолютно неупругим ударами. В качестве меры механического взаимодействия тел при ударе служит импульс силы за время удара: 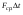 , , где 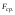 – средняя сила при ударе. – средняя сила при ударе. Из II закона Ньютона 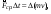 измеряя время удара измеряя время удара 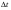 и изменение импульса тела за время удара и изменение импульса тела за время удара 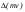 , можно определить среднюю силу удара. , можно определить среднюю силу удара.Приборы и принадлежности: прибор для исследования столкновения шаров FPM-08 или ФМ-17, линейка. Теория метода и описание прибора В настоящей работе рассматривается упругий удар шаров, подвешенных в виде маятников, причем один шар до удара покоится ( 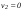 ). Удар происходит в положении, соответствующем равновесию тел, и является центральным и прямым. Применяем к ударяющимся шарам закон сохранения импульса для упругого удара ). Удар происходит в положении, соответствующем равновесию тел, и является центральным и прямым. Применяем к ударяющимся шарам закон сохранения импульса для упругого удара 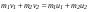 . (4.12) . (4.12)Для шаров одинаковой массы в проекциях на горизонтальное направление 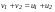 . На основании закона сохранения энергии можно записать: . На основании закона сохранения энергии можно записать: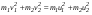 . (4.13) . (4.13)Учитывая равенство масс соударяющихся шаров, уравнение (4.13) можно записать в виде 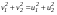 . .Решая совместно (4.12) и (4.13) с учетом равенства масс, получим:  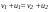 или или 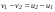 . .При упругом ударе часть кинетической энергии шаров переходит в энергию остаточной деформации, тогда 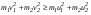 . .В этом случае для относительных скоростей получим следующее соотношение: 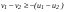 . .Относительная скорость изменит направление на противоположное, уменьшаясь по абсолютной величине. Для количественной оценки уменьшения относительной скорости вводится коэффициент восстановления скорости 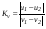 , в нашей работе , в нашей работе 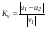 . (4.14) . (4.14)В условиях опыта Kv может считаться величиной, зависящей только от материала соударяющихся тел. Коэффициент восстановления скорости служит для характеристики упругих свойств различных материалов и может принимать значения от 0 до 1. Для реальных тел Kv<1. Не абсолютно упругий удар сопровождается остаточной деформацией. Энергию остаточной деформации можно определить из закона сохранения энергии, для одинаковых шаров получим следующее выражение: 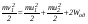 . (4.15) . (4.15)Коэффициент восстановления энергии определяется как отношение суммарной кинетической энергии тел после удара к суммарной кинетической энергии тел до удара 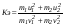 , в нашей работе , в нашей работе 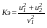 . (4.16) . (4.16)Шар, отведенный от положения равновесия на угол α (рис. 4.2), об-
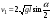 . (4.17) . (4.17)До столкновения импульс шаров определяется по формуле 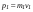 . (4.18) . (4.18)После упругого столкновения 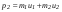 . (4.19) . (4.19)где 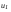 – скорость первого шара после удара, – скорость первого шара после удара, 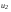 – скорость второго шара после удара. – скорость второго шара после удара. Скорости u1 и u2 находим по формулам: 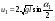 , (4.20) , (4.20)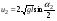 , (4.21) , (4.21)где α1 и α2 – угловое расстояние, на которое после удара переместились первый и второй шары. Порядок выполнения работы и обработка результатов измерений Задание 1. Определение коэффициентов восстановления скорости и энергии при ударе шаров
Задание 2. Определение энергии остаточной деформации
Задание 3. Проверка закона сохранения импульса для упругого удара и закона сохранения импульса и энергии для абсолютно упругого удара
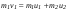 . .Обозначим 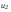 как как 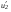 и рассчитаем его по формуле и рассчитаем его по формуле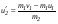 . .Расчеты занести в табл. 4.2 и сравнить экспериментальные значения 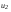 с теоретическими с теоретическими 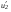 . .
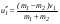 , , 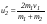 , ,занести в табл. 4.2 и сравнить со скоростями 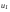 и и 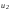 , полученными экспериментально. , полученными экспериментально.Задание 4. Определение средней силы удара
Таблица 4.2 m1 = кг; m2 = кг; l = м
Контрольные вопросы
|


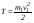 , откуда
, откуда 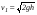 . Из ∆АВС следует
. Из ∆АВС следует 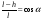 ,
, 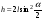 . Подставив h в уравнение для v1, получим
. Подставив h в уравнение для v1, получим 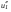 и
и 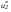 :
: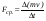 среднюю силу удара.
среднюю силу удара.