Вопрос19 Электрической ток. Характеристики электрического тока. Сила тока, вектор плотности тока, уравнение непрерывности тока. ЭДС источника тока. Напряжение.
Электри́ческий ток — направленное движение электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в полупроводниках — электроны
Хар-ки:Направление тока
Исторически принято, что направление тока совпадает с направлением движения положительного заряда в проводнике. При этом, если единственными носителями тока являются отрицательно заряженные частицы (например, электроны в металле), то направление тока противоположно направлению движения электронов.
Силой тока называется физическая величина равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени.По закону Ома сила тока I пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника RПлотностью тока называется вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярную направлению тока, к величине этой площадки, а направление вектора совпадает с направлением движения положительного заряда в токе
Согласно закону Ома плотность тока в среде j пропорциональна напряжённости электрического поля Е и проводимости среды (сигма)
мощностьПри протекании тока в проводнике совершается работа против сил сопротивления. Эта работа выделяется в виде тепла. Мощностью тепловых потерь называется величина, равная количеству выделившегося тепла в единицу времени. Согласно закону Джоуля — Ленца мощность тепловых потерь в проводнике пропорциональна силе протекающего тока и приложенному напряжению:
Мощность измеряется в ваттах.В сплошной среде объёмная мощность потерь p определяется скалярным произведением вектора плотности тока j и вектора напряжённости электрического поля Е в данной точке: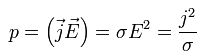
В электродинамике уравнение непрерывности выводится из уравнений Максвелла. Оно утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус, 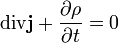
Электродвижущая сила (ЭДС) источника тока равна работе, которую совершают сторонние силы по перемещению единичного положительного электрического заряда вдоль всей цепи.E=Act\q ,q - переносимый заряд,Аст - работа сторонних сил
Напряже́ние (разность потенциалов, падение потенциалов) между точками A и B — отношение работы электрического поля при переносе пробного электрического заряда из точки A в точку B к величине пробного заряда.
|
Вопрос20 Закон Ома для однородного участка цепи, электрическое сопротивление, удельное сопротивление, зависимость сопротивления проводников от температуры.
закон Ома для однородного участка цепи:
ТОК, ТЕКУЩИЙ ПО ОДНОРОДНОМУ МЕТАЛЛИЧЕСКОМУ ПРОВОДНИКУ, ПРОПОРЦИОНАЛЕН ПАДЕНИЮ НАПРЯЖЕНИЯ U НА ПРОВОДНИКЕ", т. е.
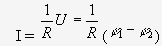
где R - сопротивление проводника, измеряется в СИ в омах ( Ом); из (14) следует, что 1Ом =1 В/1 А.
Сопротивление проводника R =ρl / S ,
где р - удельное сопротивление, измеряется в СИ в Ом × м.
Оно зависит от температуры:фи =фи0а T , где фи0 - удельное сопротивление при температуре t = 0¦С, а- температурный коэффициент сопротивления, близкий к 1/273 К-1, T- термодинамическая температура ; так что с ростом температуры
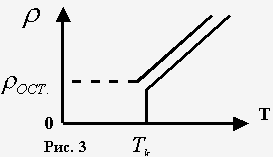
Cопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.3
 Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется. Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной , сопротивление проводника равно , а при температуре оно равно , то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры: .
Коэффициент пропорциональности называют температурным коэффициентом сопротивления. Он характеризует зависимость сопротивления вещества от температуры. Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К. Для всех металлических проводников и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов .
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры: .
Так как мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 1).
Хотя коэффициент довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов просто необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем, температурный коэффициент сопротивления очень мал: ; удельное сопротивление константана велико: . Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т.е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве основного рабочего элемента такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Удельное сопротивление металлов растет линейно с увеличением температуры. У растворов электролитов оно уменьшается при увеличении температуры.
|
Вопрос21. Закон Ома в дифференциальной форме. Удельная электропроводность.
Закон Ома в дифференциальной форме
Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: 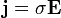
где:
— вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Уде́льная проводи́мость (уде́льная электропрово́дность) — мера способности вещества проводить электрический ток. (Точнее следует говорить об электропроводности среды, т.к. не имеется в виду обязательно химически чистое вещество; эта величина различна для разных веществ или смесей, сплавов и т.п.). В линейном изотропном веществе плотность возникающего тока прямо пропорциональна электрическому полю (см. Закон Ома): 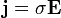
где:
В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, т.е. не совпадает в различных точках проводника.В анизотропных средах формула остаётся той же, но σ является тензором 2 ранга, и векторы плотности тока и напряжённости поля, вообще говоря, не коллинеарны.Величина, обратная удельной проводимости, называется удельным сопротивлением.Вообще говоря, линейное соотношение, написанное выше, верно в лучшем случае приближённо, причём приближение это хорошо только для сравнительно малых значений E. Впрочем, и при тех значениях E, когда отклонения от линейности есть, но не слишком велики, удельная электропроводность может сохранять свою роль в качестве коэффициента при линейном члене разложения.В системе СИ удельная электропроводность измеряется в сименсах на метр (См/м) или в Ом−1·м−1. В СГСЭ единицей удельной электропроводности является обратная секунда (с−1).
|
Вопрос22. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи.
На неоднородном участке цепи плотность тока пропорциональна сумме напряжен -ностей электростатического поля и поля сторонних сил, т.е 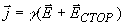 .Рассмотрим цилиндрический проводник длиной / с площадью поперечного сечения S. Умножим обе части равенства (19) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l: .Рассмотрим цилиндрический проводник длиной / с площадью поперечного сечения S. Умножим обе части равенства (19) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
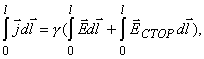 что дает j*L=(+ что дает j*L=(+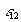 ). (20)Заменив j на I/S, а на , из (20) получим I = + ). (20)Заменив j на I/S, а на , из (20) получим I = + 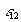 , откуда следует закон Ома для неоднородного участка цепи I = ( + , откуда следует закон Ома для неоднородного участка цепи I = ( +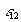 ) / R12 (21) где R12 = l / S - сопротивление участка цепи 12. Для замкнутой цепи формула (21) запишется в виде I = / R ) / R12 (21) где R12 = l / S - сопротивление участка цепи 12. Для замкнутой цепи формула (21) запишется в виде I = / R (22)где R (22)где R - суммарное сопротивление всей цепи; - ЭДС источника. - суммарное сопротивление всей цепи; - ЭДС источника.
Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС и внутренним сопротивлением r ,а также внешней цепи потребителя, имеющей сопротивление R. Согласно (22) I = / (R + r). (23) Разность потенциалов на электродах источника, рис. 5, равна напряжению на внешнем участке цепи: U = = IR = - Ir . (24)Если цепь разомкнуть, то ток в ней прекратится и напряжение U на зажимах источника станет равным его ЭДС, т.е. U = .Таким образом, напряжение на внешнем участке цепи, рис. 5, будет равно U = IR = R / (R + r). (25)В пределе, когда R0 (источник тока замкнут накоротко), то в этом случае, в соответствии с (23), ток максималенIмакс = / R , (26)а напряжение во внешней цепи равно нулю.В противоположном предельном случае, R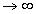 , цепь разомкнута и ток отсутствует: I=lim[ / (R+r)]=0, а напряжение на зажимах источника , цепь разомкнута и ток отсутствует: I=lim[ / (R+r)]=0, а напряжение на зажимах источника
максимально и равно его ЭДС: U = R / (R + r)= , т. к. limR / (R + r) = 1. (27)
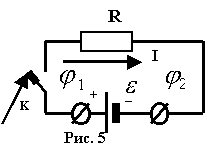  Замкнутая полная цепь имеет вид: (второй сверху)здесь Замкнутая полная цепь имеет вид: (второй сверху)здесь
R - внешнее сопротивление (общее сопротивление устройств и соединительных проводов, включенных в электрическую цепь);r - внутреннее сопротивление ( электросопротивление источника тока).
Напряжение в замкнутой цепи равно электродвижущей силе источника (тема 1). Полное сопротивление цепи складывается из внешнего и внутреннего сопротивления. Поэтому "сила тока в замкнутой цепи равна отношению э.д.с. к ее полному сопротивлению":I = e / (R + r) . (11)Формула (11) представляет собой закон Ома для замкнутой цепи.Из (11) следует, что e = I*R + I*r. Таким образом э.д.с. равна сумме падения напряжений во внешней и внутренней цепи.
|
Вопрос23. Закон Джоуля-Ленца. Работа и мощность тока. КПД источника тока.
Проводник нагревается, если по нему протекает электрический ток. Джоуль и Ленц установили, что количество выделившегося тепла Q = I2 Rt, (28)
где I - ток, R - сопротивление, t - время протекания тока. Легко доказать, что
Q = I2 Rt = UIt = U2t/R = qU, (29) где q = It - электрический заряд.
Если ток изменяется со временем (т. е. в случае непостоянного тока), то
Q = = , (30)где i - мгновенное значение тока.
Нагревание проводника происходит за счет работы, совершаемой силами электрического поля над носителями заряда. Эта работа
A = qU = UIt =I2 Rt = U2 t / R . (31)Работа А, энергия W , количество тепла Q в СИ измеряются в Дж.Так как мощность характеризует работу, совершаемую в единицу времени, т.е.
Р = , то P = UI = I2 R = U2 / R . (32) Мощность в СИ измеряется в ваттах: 1 Вт = 1 Дж / 1 с; откуда 1 Дж = 1 Втс; 3600 Дж = 1Вт час, 3,6 •106 Дж = 1 кВт час.Формулы (31) и (32) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам
Aзатр = q = It = I2 (R + r)t = t.(33)
Pзатр= = I = I2 (R + r) = . (34)
Отношение полезной работы (мощности) к затраченной характеризует КПД источника
= = = . (35)
|
Вопрос24. Закон Джоуля-Ленца в дифференциальной форме.
Согласно закону Джоуля - Ленца (28) в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло
dQ =I2 Rdt =(jdS)2 = j2 dldSdt = j2 dVdt.
Разделив на dV и dt, найдем количество тепла, выделяющееся в единицу времени в единице объема Qуд = = j2 . (37)
здесь Qуд -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
С учетом (16) из (37) следует, что Qуд = j2 = 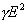 . (38) . (38)
Формулы (37) и (38) выражают закон Джоуля - Ленца в дифференциальной форме.
|
Вопрос25. Магнитное поле в вакууме. Контур с током в магнитном поле. Вектор магнитной индукции. Силовые линии магнитного поля. Закон Ампера.
Магнитным полем называется одна из форм проявления электромагнитного поля.
Магнитное поле создается движущимися электрическими зарядами, частицами и телами, облалающими магнитным моментом, а также изменяющимся во времени электрическим полем.
Магнитное поле характеризуется вектором напряженности Н.
Магнитное поле действует только на движущиеся электрические заряды и на частицы и тела, облалающими магнитным моментом.
Силовой характеристикой магнитного поля является вектор магнитной индукции В (вектор индукции магнитного поля), который определяется:
-по действию магнитного поля на движущуюся в нем заряженную частицу – точечный электрический заряд;
-малый элемент проводника с током;
-по действию магнитного поля на небольшую рамку с током.
Магнитное поле изображается силовыми линиями магнитной индукции, по аналогии с силовыми линиями напряженности электрического поля.
Направление силовых линий магнитного поля – от северного полюса к южному, а касательная к силовым линиям магнитного поля совпадает с направлением вектора магнитной индукции. Линии магнитной индукции нигде не обрываются: они либо замкнуты, либо идут в бесконечность.
Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности магнитного поля соотношением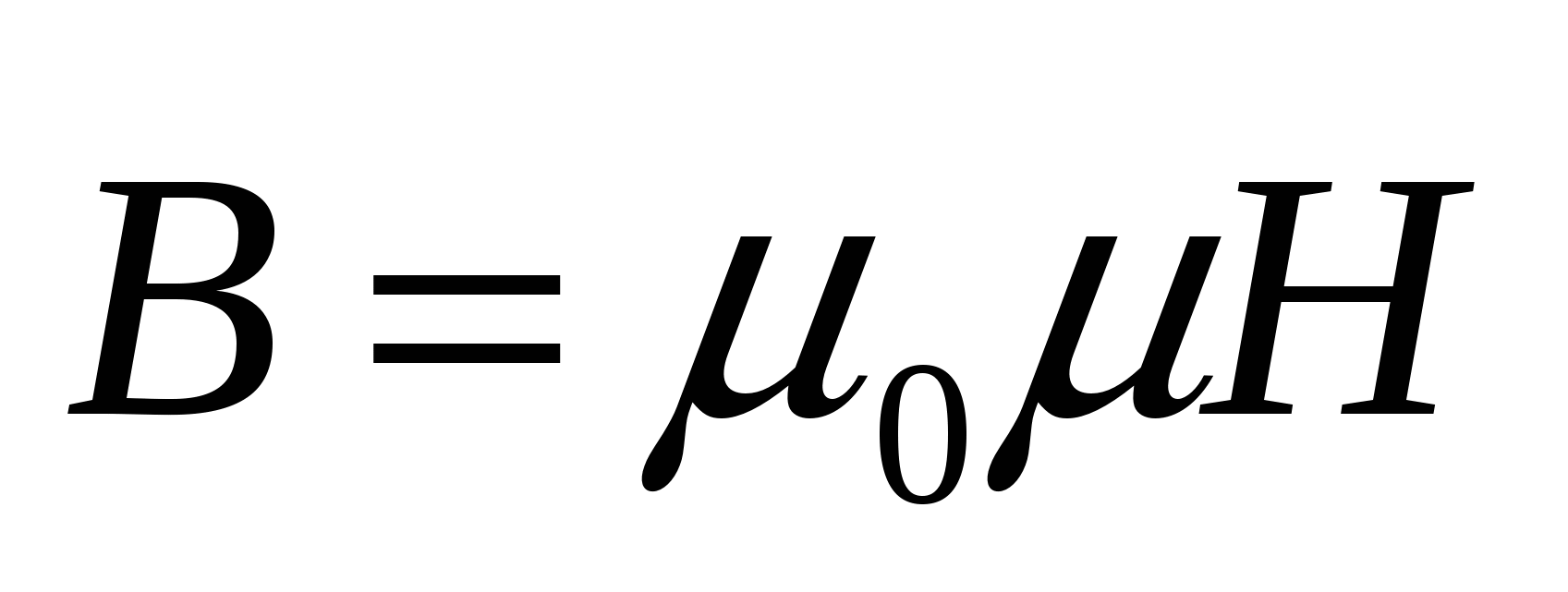 , где , где 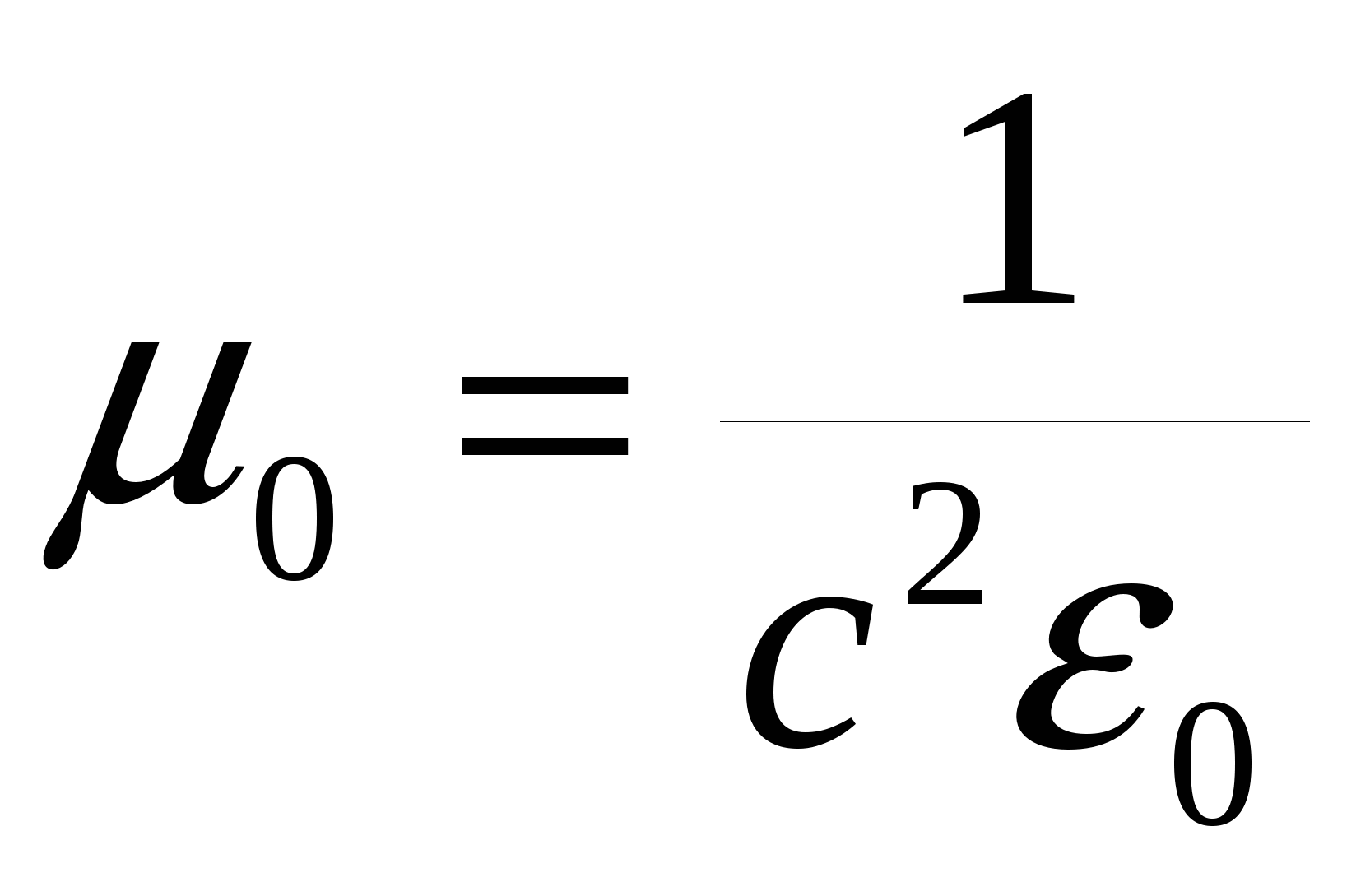 – магнитная постоянная; μ – магнитная проницаемость среды. Магнитное поле считается однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение. – магнитная постоянная; μ – магнитная проницаемость среды. Магнитное поле считается однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.
В магнитном поле на элемент проводника dl с током I действует сила dF, которая равна
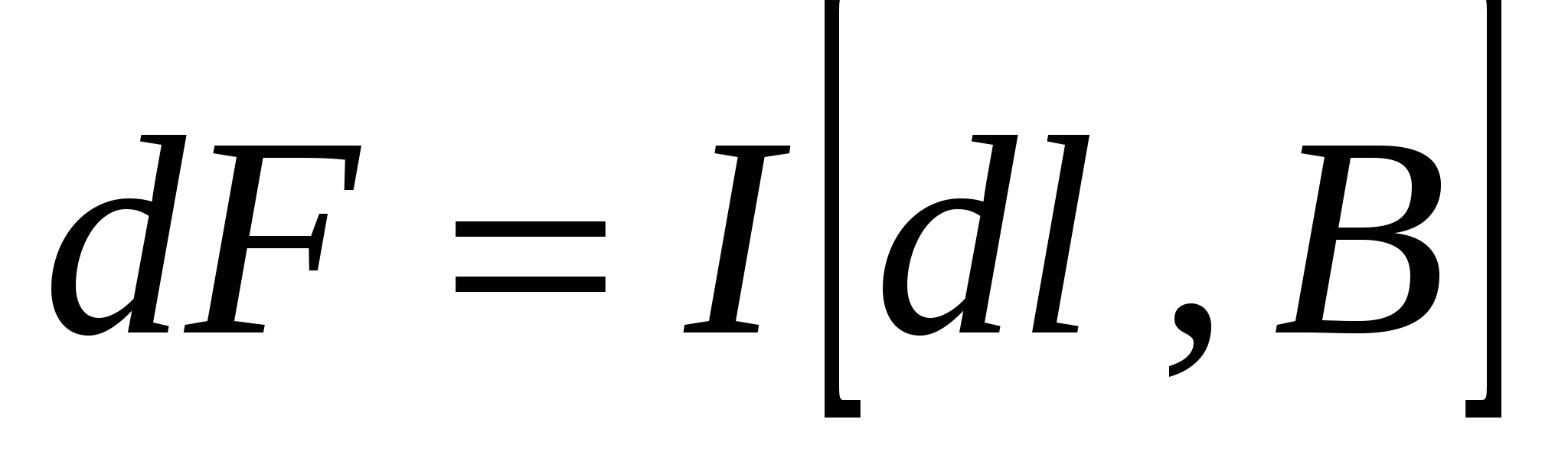 → → 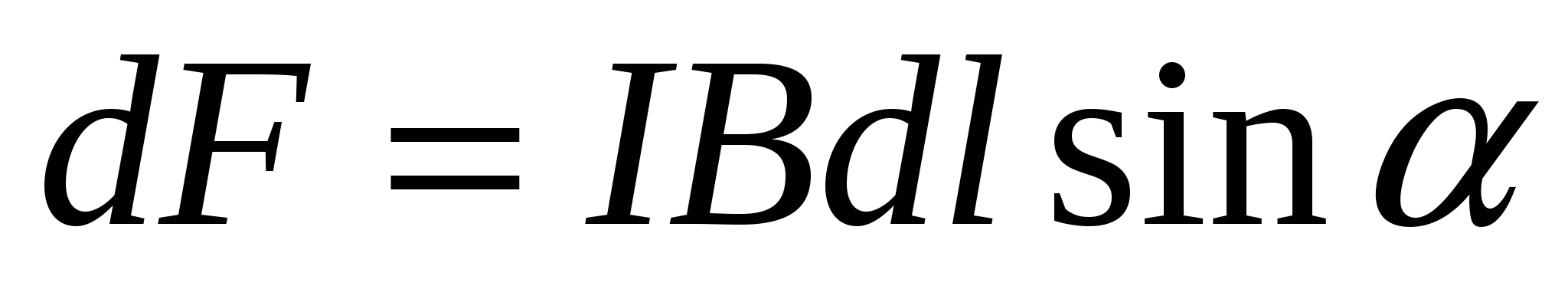
(закон Ампера)
Направление вектора действия силы определяется по правилу левой руки: если расположить левую ладонь так, что в нее входит вектор В, а по направлению четырех пальцев течет ток, то отогнутый в сторону большой палец укажет направление силы, действующей на проводник с током.
|
Вопрос26. Закон Био-Савара-Лапласа. Применение закона к вычислению магнитных полей прямолинейного проводника с током и кругового тока.
Био, Савар и Лаплас установили закон, который позволяет вычислить магнитную индукцию поля, созданного элементом тока Idl на расстоянии r от него:
dB = , (5)
т.е. индукция магнитного поля, создаваемого элементом тока Idl точке А, (см. рис. 3), на расстоянии r от него, пропорциональна величине элемента тока и синусу угла a, равного углу между направлениями элемента тока Idl и r , а также обратно пропорциональна квадрату расстояния между ними; Гн / м - магнитная постоянная.
Из рис. 4 с учетом (6) находим, что d 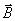 плоскости, в которой лежат dl и r ; далее можно найти ,откуда, принимая во внимание, что получаем плоскости, в которой лежат dl и r ; далее можно найти ,откуда, принимая во внимание, что получаем 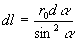 . С учетом этого из (5) находим: . С учетом этого из (5) находим:
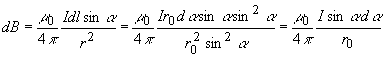
интегрируя последнее равенство, получаем:
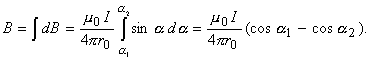 (8) (8)
Для бесконечно длинного проводника , и из (8) следует, что
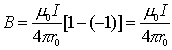 *2 (9) *2 (9)
C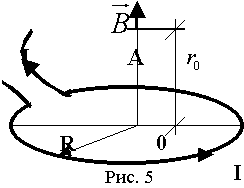 учетом (4) и (9) cила взаимодействия двух бесконечно длинных тонких и параллельных проводников учетом (4) и (9) cила взаимодействия двух бесконечно длинных тонких и параллельных проводников 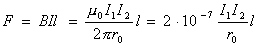 . (10) . (10)
Пусть I1 = I2 = I, r0 = 1м, l = 1м, F =2*10-7 Н, тогда I = 1 А. Это было строгое определение единицы силы тока - ампера.
М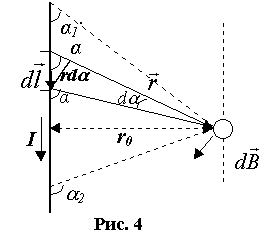 ожно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (см. рис.5), будет ожно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (см. рис.5), будет 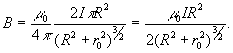 (11) (11)
В частности, в центре кругового тока ,
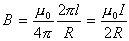 . (12) . (12)
Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки
.(13)
При больших расстояниях от контура, (рис. 5), т. е. при r0 >> R из (11) получим
(14)
|
Вопрос27. Магнитный момент контура с током. Момент сил, действующих на контур с током в магнитном поле. Энергия магнитного диполя в магнитном поле.
Магнитным моментом контура с током I называется векторная величина pm, равная
г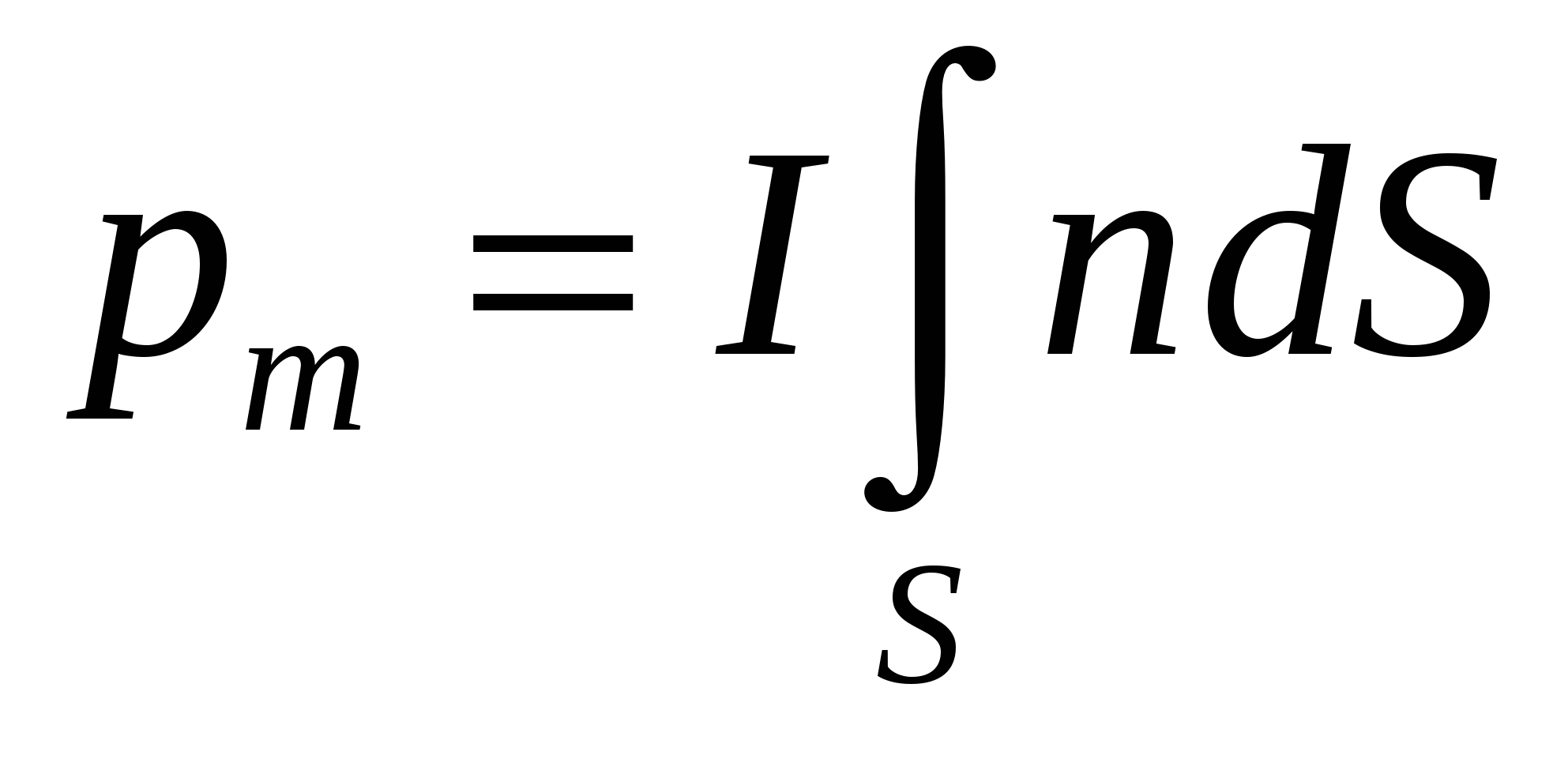 де n – единичный вектор нормали к элементу dS поверхности S, ограниченной контуром с током. де n – единичный вектор нормали к элементу dS поверхности S, ограниченной контуром с током.
З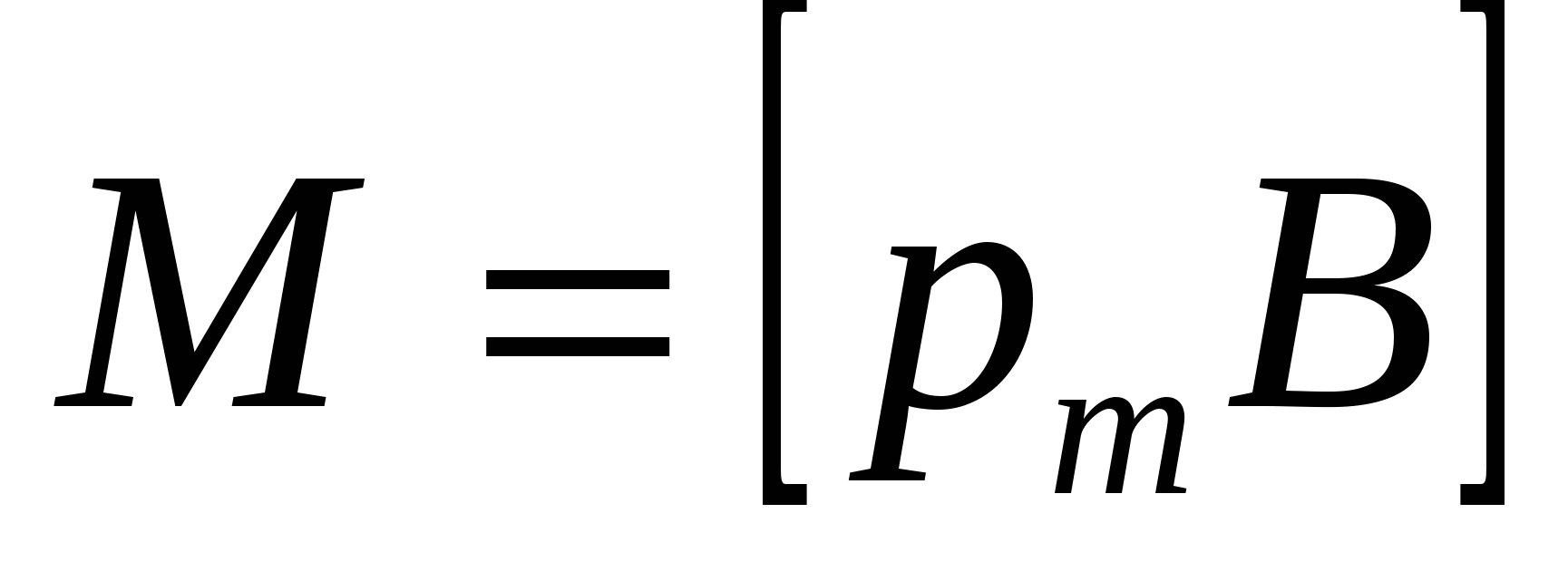 амкнутый контур с током в однородном магнитном поле испытывает действие вращающего момента сил М амкнутый контур с током в однородном магнитном поле испытывает действие вращающего момента сил М
где pm – вектор магнитного момента контура с током, В – вектор магнитной индукции поля.
Энергия магнитного диполя в магнитном поле 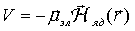 - энергия электрона в магнитном поле, создаваемом ядром. - энергия электрона в магнитном поле, создаваемом ядром.
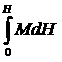 - ее изменение - ее изменение
|
Вопрос28. Теорема о циркуляции вектора магнитной индукции (закон полного тока). Вихревой характер магнитного поля. Применение теоремы о циркуляции к расчету магнитного поля соленоида.
Теорема о циркуляции утверждает, что циркуляция вектора В магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
Циркуляцией вектора магнитной индукции В по заданному контуру называется интеграл
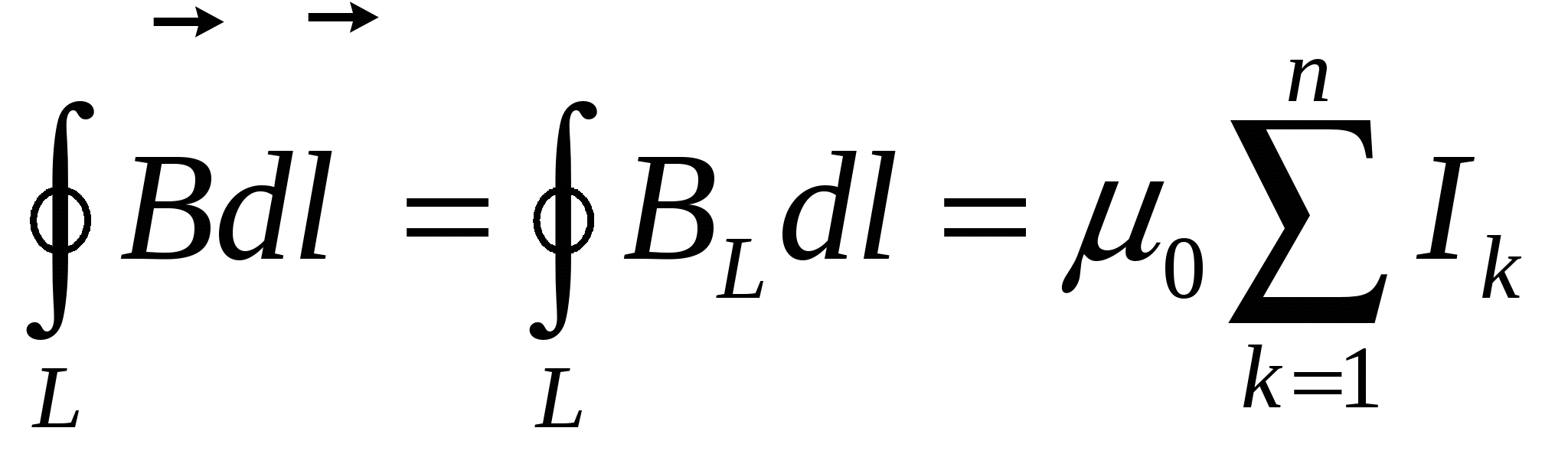
закон полного тока для магнитного поля в вакууме
(теорема о циркуляции вектора магнитной индукции)
где n – число проводников с токами, охватываемых контуром L произвольной формы.
Вихревой характер магнитного поля. Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического. Магнитное поле соленоида. Пусть соленоид длиной l, во много раз превышающей его диаметр, имеет N витков, по которым течет ток силой I. Если соленоид находится в вакууме (или воздухе), то магнитная индукция поля в нем численно равна B0 = μ0 IN / l = μ0 In,n где n = N/l; In – число ампер-витков, приходящихся на единицу длины соленоида; μ0 – магнитная постоянная, характеризующая магнитное поле в вакууме. Поле внутри длинного соленоида однородно и направлено от южного полюса (S) к северному (N). Модуль магнитной индукции поля в соленоиде пропорционален числу ампервитков, приходящихся на единицу его длины. Магнитная постоянная μ0 = 4π · 10-7 кг · м/(с2 · А2).
|
Вопрос29. Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля в вакууме.
Потоком вектора магнитной индукции (магнитным потоком) dФ сквозь малую поверхность плошадью dS называется скалярная величина
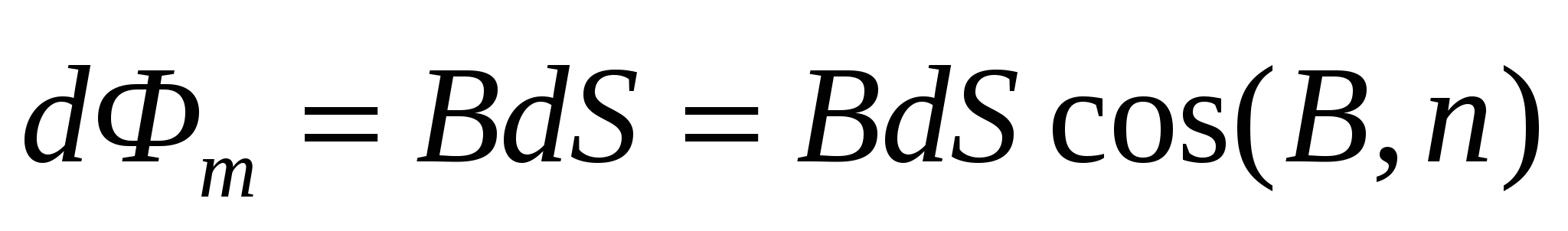
Сквозь произвольную поверхность S магнитный поток равен
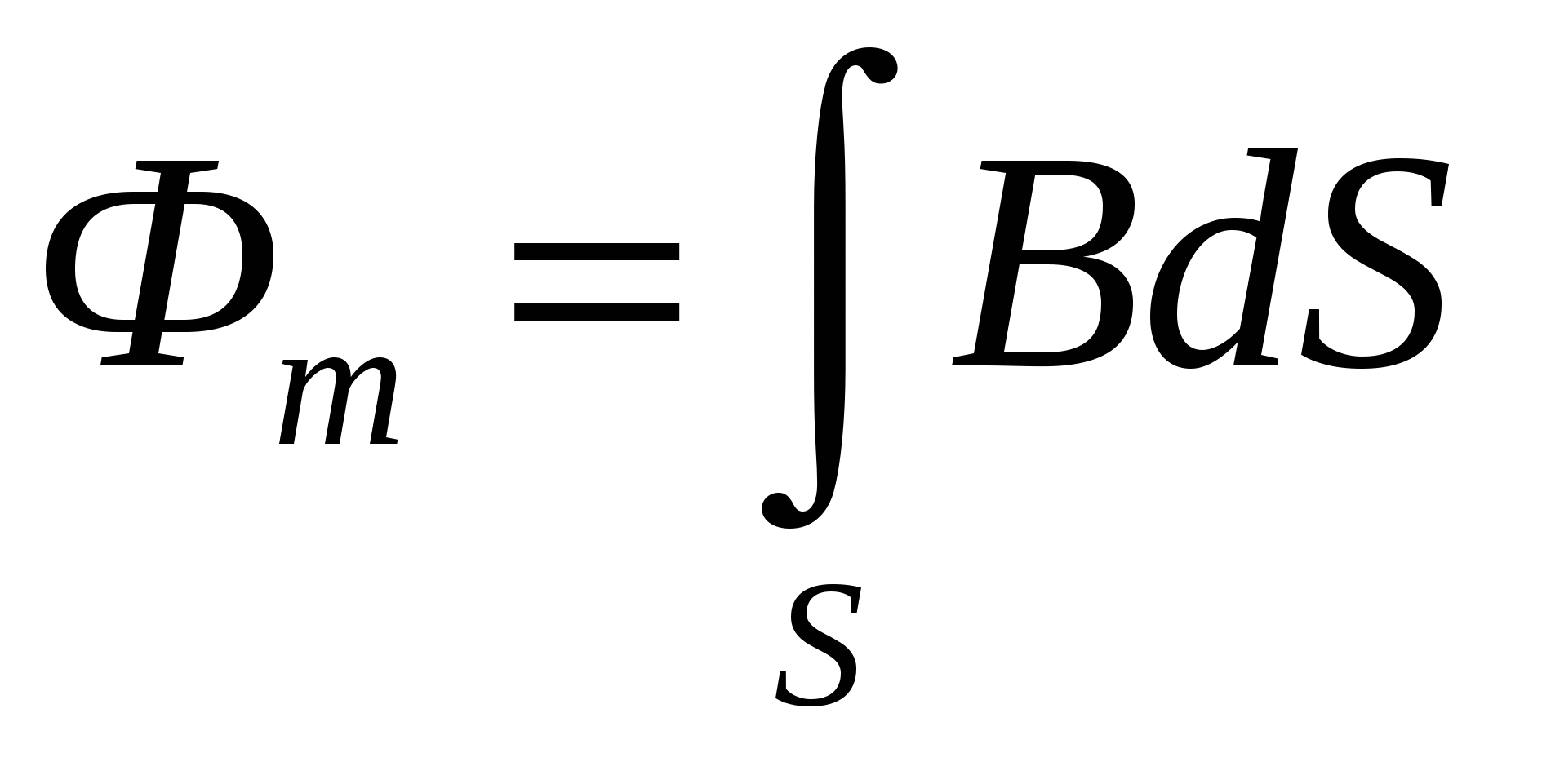
Магнитный поток сквозь произвольную замкнутую поверхность равен нулю
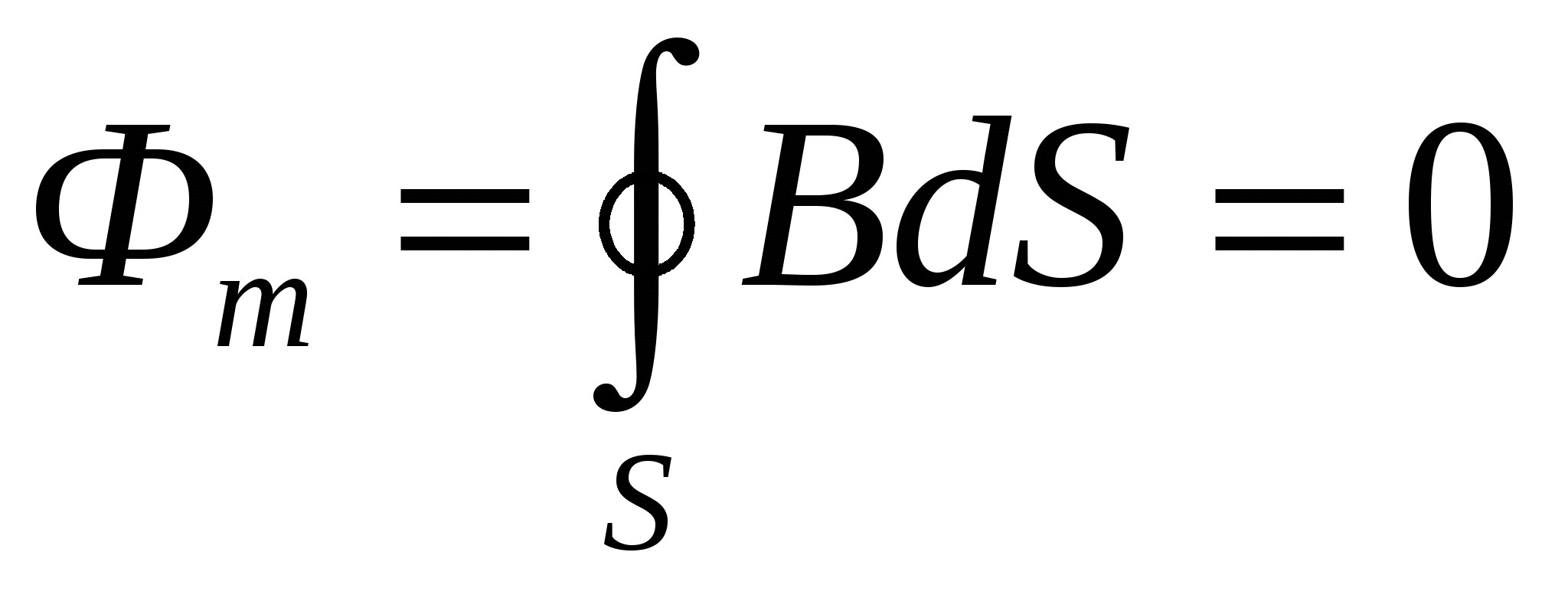
(теорема Остроградского-Гаусса для магнитного поля)
Этот результат означает, что в природе не существует "магнитных зарядов" – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции.
|
Вопрос30. Работа при перемещении проводника с током в постоянном магнитном поле.
На проводник с током в магнитном поле действует сила
ампера. Если проводник не прикреплен, то под действием
этой силы ток будет перемещаться и совершает работу.
Вычислим ее: Fa=IBl; dA=Fa dx=IBldx=IBdS; dS=ldx; dS=ldx;
BdS=dФm; dA=IdФm; A12=∫[1 - 2] IdФm; Если при перемещении проводника y=const, то A12=J(Ф2 – Ф1). Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
| |
 Скачать 1.21 Mb.
Скачать 1.21 Mb.