Вопрос40. Свободные незатухающие электромагнитные колебания в колебательном контуре. Дифференциальное уравнение незатухающих колебаний, его решение и анализ (закон сохранения энергии).
Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:
Т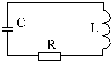 акую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими. акую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.
Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями. Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону: , (1) или 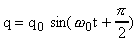 , (2) , (2)
где : q - мгновенное значение заряда конденсатора; q0 - амплитудное значение электрического заряда; w0 - собственная частота колебаний в контуре.
Форма записи (через cos или sin) не имеет значения, так как отличие будет определяться лишь начальными условиями, а именно различной начальной фазой колебаний. Зная связь между зарядом конденсатора и разностью потенциалов на его обкладках: С=q/U, (3) можно аналогично записать гармонические колебания разности потенциалов: U=U0cos(w0t) , (4) или U=U0sin(w0t+pi/2), (5) где: U - мгновенное значение напряжения на обкладках конденсатора;
U0 - амплитудное значение напряжения; w0 - собственная частота колебаний в контуре.
Продифференцировав (1)получим, Сила тока является первой производной от электрического заряда по времени: I=q/t . (6) Поэтому гармонические колебания силы тока в колебательном контуре будут происходить по закону: i=I0sin(w0t)=I0cos(w0t+pi/2), (7) где: i - мгновенное значение тока в контуре;
I0 = q0 w0 - амплитудное значение тока; w0 - собственная частота колебаний в контуре.
Циклическая частота w0 называется собственной частотой электромагнитных колебаний, она зависит только от параметров колебательного контура, а именно - от емкости конденсатора С и индуктивности L: . (8) Период собственных электромагнитных колебаний, соответственно, вычисляется по формуле: . (9)
Эта формула была впервые получена английским ученым В.Томсоном и называется формулой Томсона.
Физические процессы, происходящие в колебательном контуре, сопровождается непрерывными преобразованиями одного вида энергии в другой, а именно: энергия электрического заряда конденсатора превращается в энергию магнитного поля катушки и наоборот. При этом, в полном соответствии с законом сохранения и превращения энергии, полная энергия в колебательном контуре остается величиной постоянной: , (10)
г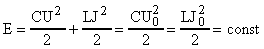 де: U и J - соответственно напряжение на обкладках конденсатора и сила тока в контуре в любой момент времени; U0 и J0 - амплитудные (максимальные) значения этих же величин. де: U и J - соответственно напряжение на обкладках конденсатора и сила тока в контуре в любой момент времени; U0 и J0 - амплитудные (максимальные) значения этих же величин.
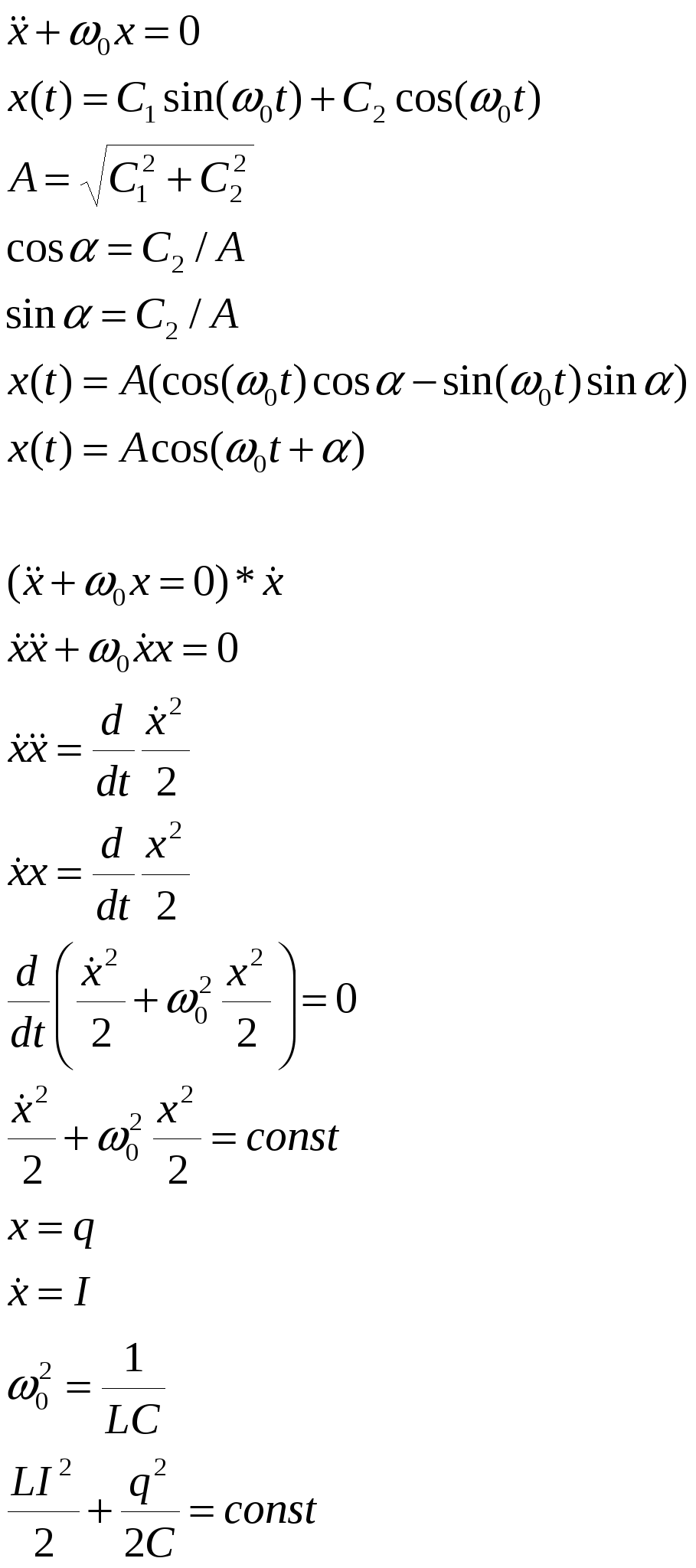
Первое – энергия магнитного поля в катушке, второе – энергия м. поля в конденсаторе
|
Вопрос41. Вынужденные электромагнитные колебания. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Явление резонанса.
Вынужденными колебаниями называют такие колебания, которые вызываются действием на систему внешних сил, периодически изменяющихся с течением времени. В случае электромагнитных колебаний такой внешней силой является периодически изменяющаяся э.д.с. источника тока. Отличительные особенности вынужденных колебаний: вынужденные колебания - незатухающие колебания; частота вынужденных колебаний равна частоте внешнего периодического воздействия на колебательную систему, т.е., в данном случае, равна частоте изменения э.д.с. источника тока.
Амплитуда вынужденных колебаний зависит от частоты изменения э.д.с. источника тока. Для вынужденных колебаний характерно явление электрического резонанса, при котором амплитуда вынужденных колебаний становится максимальной. Это физическое явление наблюдается при совпадении частоты изменения э.д.с. источника тока с собственной частотой колебаний данного контура, т.е.: , (1)
где: i - мгновенное значение тока, т.е. его значение в момент времени t = 0; J0 - амплитудное или максимальное значение силы тока; w - частота изменения тока, численно равная частоте изменения э.д.с. источника тока. Мгновенным или амплитудным значениями тока и напряжения на практике пользоваться неудобно. Амперметры и вольтметры в цепи переменного тока измеряют так называемые действующие или эффективные значения
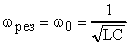 переменного тока, которые связаны с амплитудными значениями тока по формулам: переменного тока, которые связаны с амплитудными значениями тока по формулам:
, (4) . (5) Действующими значениями силы тока и напряжения переменного тока называют значения этих величин для такого постоянного тока, который на том же активном сопротивлении выделяет за время, равное периоду Т переменного тока, такое же количество теплоты, как и данный переменный ток.
Источником переменного тока является генератор переменного тока, физический принцип действия которого основан на равномерном вращении с угловой скоростью w плоской рамки площадью S, состоящей из N витков, в однородном магнитном поле с индукцией В. При этом рамку пронизывает переменный магнитный поток:
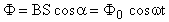 , (6) где: Ф0 - максимальное значение магнитного потока; a - угол между нормалью к рамке и вектором магнитной индукции В; w - угловая скорость вращения рамки. Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22) где , (6) где: Ф0 - максимальное значение магнитного потока; a - угол между нормалью к рамке и вектором магнитной индукции В; w - угловая скорость вращения рамки. Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22) где 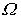 - круговая частота вынуждающей силы. Дифференциальное уравнение вынужденных колебаний с учетом затухания запишется в виде: m(d2x/dt2) = -kx - r(dx/dt) + Fmcos - круговая частота вынуждающей силы. Дифференциальное уравнение вынужденных колебаний с учетом затухания запишется в виде: m(d2x/dt2) = -kx - r(dx/dt) + Fmcos 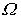 t. t.
Перепишем это уравнение в виде: 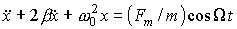 . (23) . (23)
Бета=Сопротивление деленное на 2*индуктивность
Т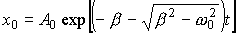 аким образом, получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением такого уравнения будет , где - общее решение однородного уравнения (23), (т. е. уравнения (23) с правой частью, равной нулю). Согласно (17) аким образом, получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением такого уравнения будет , где - общее решение однородного уравнения (23), (т. е. уравнения (23) с правой частью, равной нулю). Согласно (17)
и с течением времени . Поэтому .
Из решения (23) =>, что 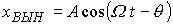 (24) где , (24) где , 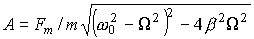 (25) (25) 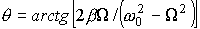 . (26) . (26)
 Из анализа (25) следует, что хотя амплитуда вынуждающей силы Fm, остается постоянной, амплитуда А вынужденных колебаний зависит от частоты вынуждающей силы. Из анализа (25) следует, что хотя амплитуда вынуждающей силы Fm, остается постоянной, амплитуда А вынужденных колебаний зависит от частоты вынуждающей силы.
И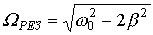 сследуя (25) на экстремум, можно показать, что только при резонансной частоте сследуя (25) на экстремум, можно показать, что только при резонансной частоте
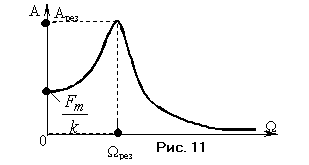
а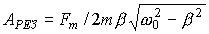 мплитуда вынужденных колебаний достигает максимальной величины: . (28) мплитуда вынужденных колебаний достигает максимальной величины: . (28)
Это явление называется резонансом. На рис. 11 приведена зависимость амплитуды А вынужденных колебаний от частоты 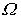 вынуждающей силы , которая определяется формулой (25); (откуда: при вынуждающей силы , которая определяется формулой (25); (откуда: при 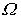 = 0 находим = 0 находим 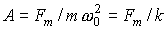 , а при имеем , что объясняется инерционностью колебательной системы). Явление резонанса, состоящее в резком увеличении амплитуды колебаний при приближении частоты вынуждающей силы к резонансной частоте, широко используется в технике. Его следует учитывать при конструировании машин, кораблей, самолетов и т.д. Необходимо, чтобы их резонансные частоты не совпадали с частотой вынуждающих внешних воздействий. , а при имеем , что объясняется инерционностью колебательной системы). Явление резонанса, состоящее в резком увеличении амплитуды колебаний при приближении частоты вынуждающей силы к резонансной частоте, широко используется в технике. Его следует учитывать при конструировании машин, кораблей, самолетов и т.д. Необходимо, чтобы их резонансные частоты не совпадали с частотой вынуждающих внешних воздействий.
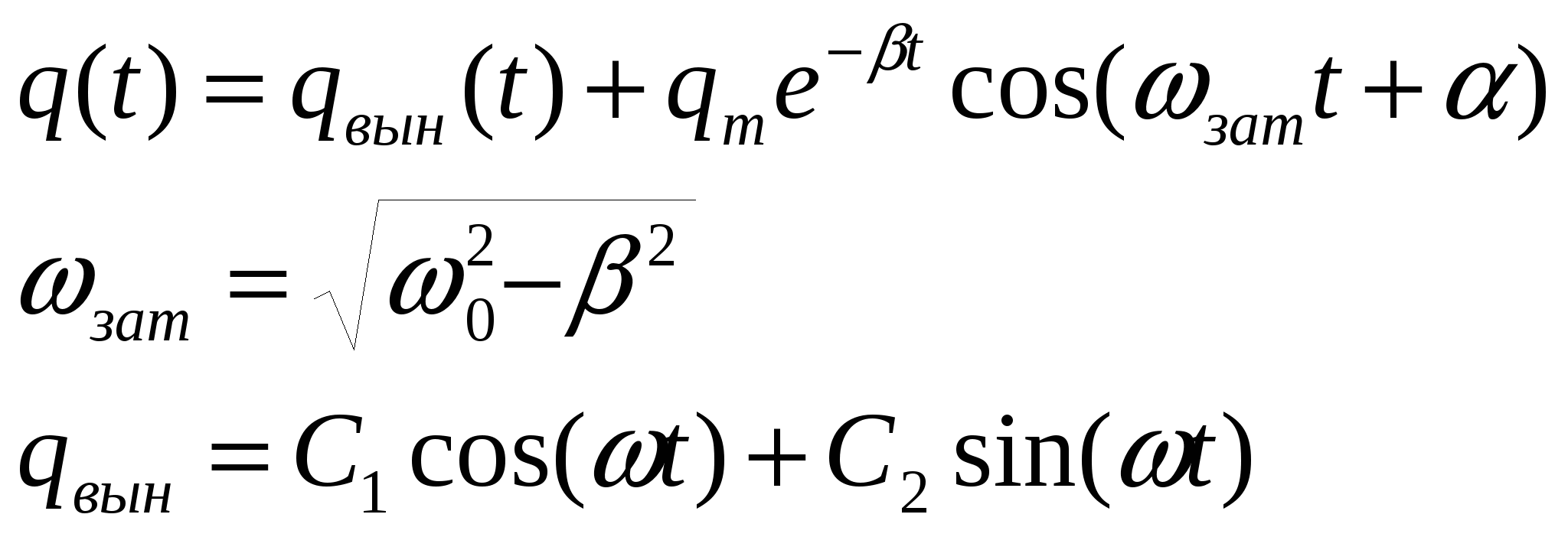 решение уравнения решение уравнения
|
Вопрос42.Обобщение закона электромагнитной индукции. Вихревое электрическое поле. Первое уравнение Максвелла.
Вихревое электрическое поле – электрическое поле, созданное изменяющимся магнитным полем. Не связано с зарядами, поэтому силовые линии являются замкнутыми.
Первое уравнение Максвелла является обобщением закона электромагнитной индукции, которое в интегральной форме имеет вид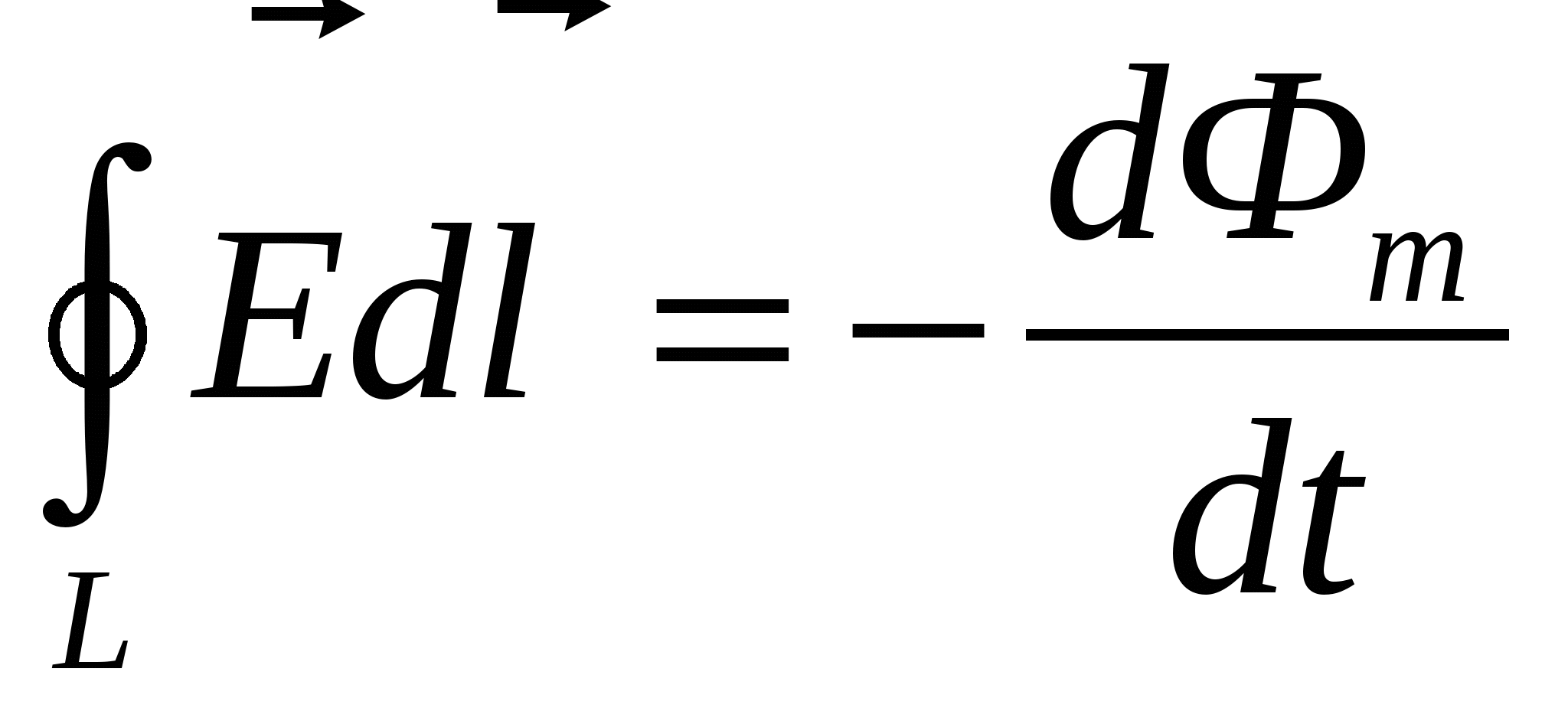 . Из выражения для магнитного потока следует . Из выражения для магнитного потока следует 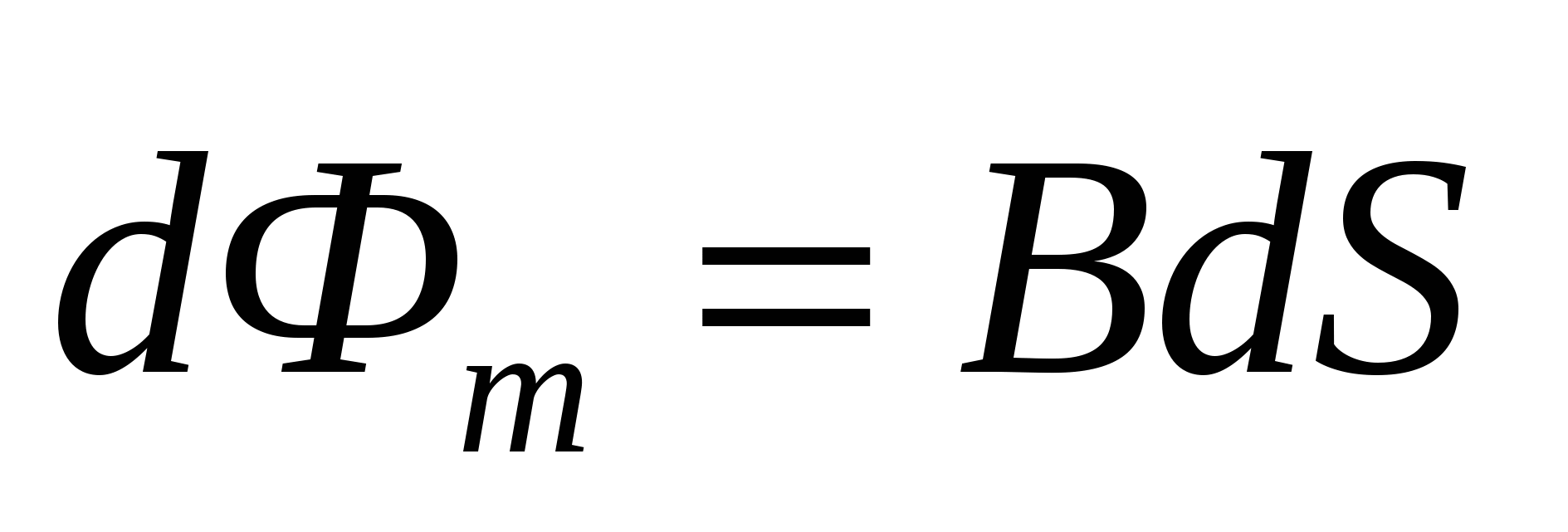 → →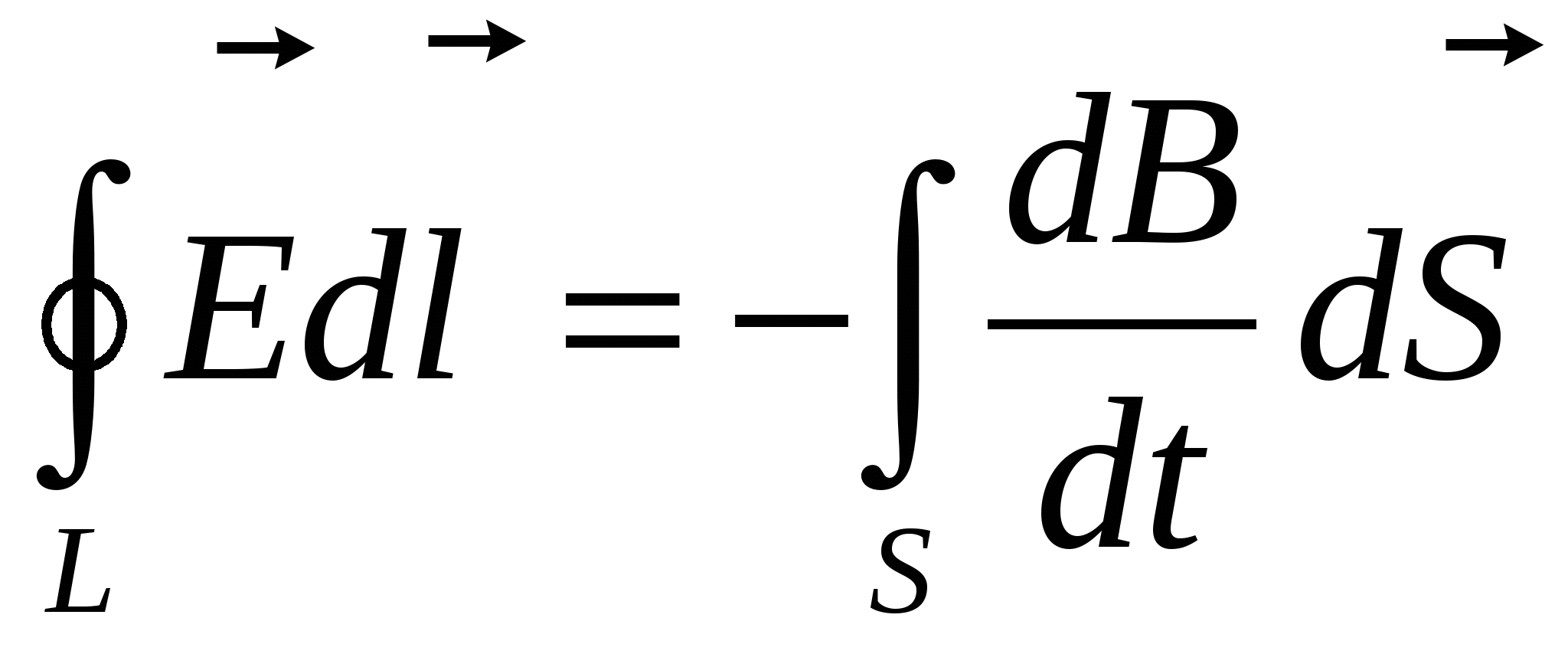 . Интеграл в правой части является функцией только от времени. Неравенство нулю циркуляции вектора напряженности электрического поля по замкнутому контуру означает, что возбуждаемое переменным магнитным полем электрическое поле является вихревым, как и само магнитное поле. . Интеграл в правой части является функцией только от времени. Неравенство нулю циркуляции вектора напряженности электрического поля по замкнутому контуру означает, что возбуждаемое переменным магнитным полем электрическое поле является вихревым, как и само магнитное поле.
Первое уравнение Максвелла – электростатическое поле создается неподвижными зарядами
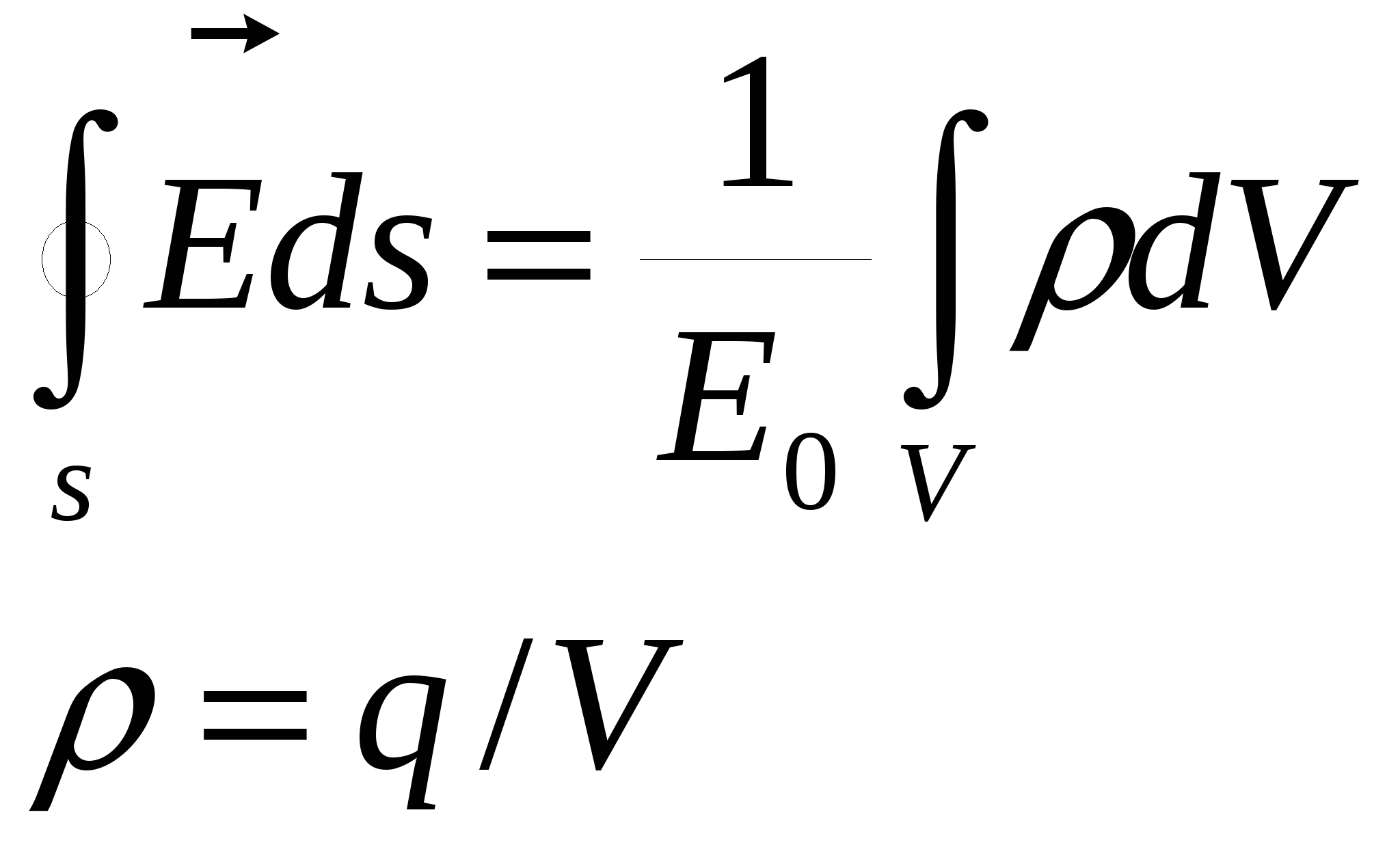
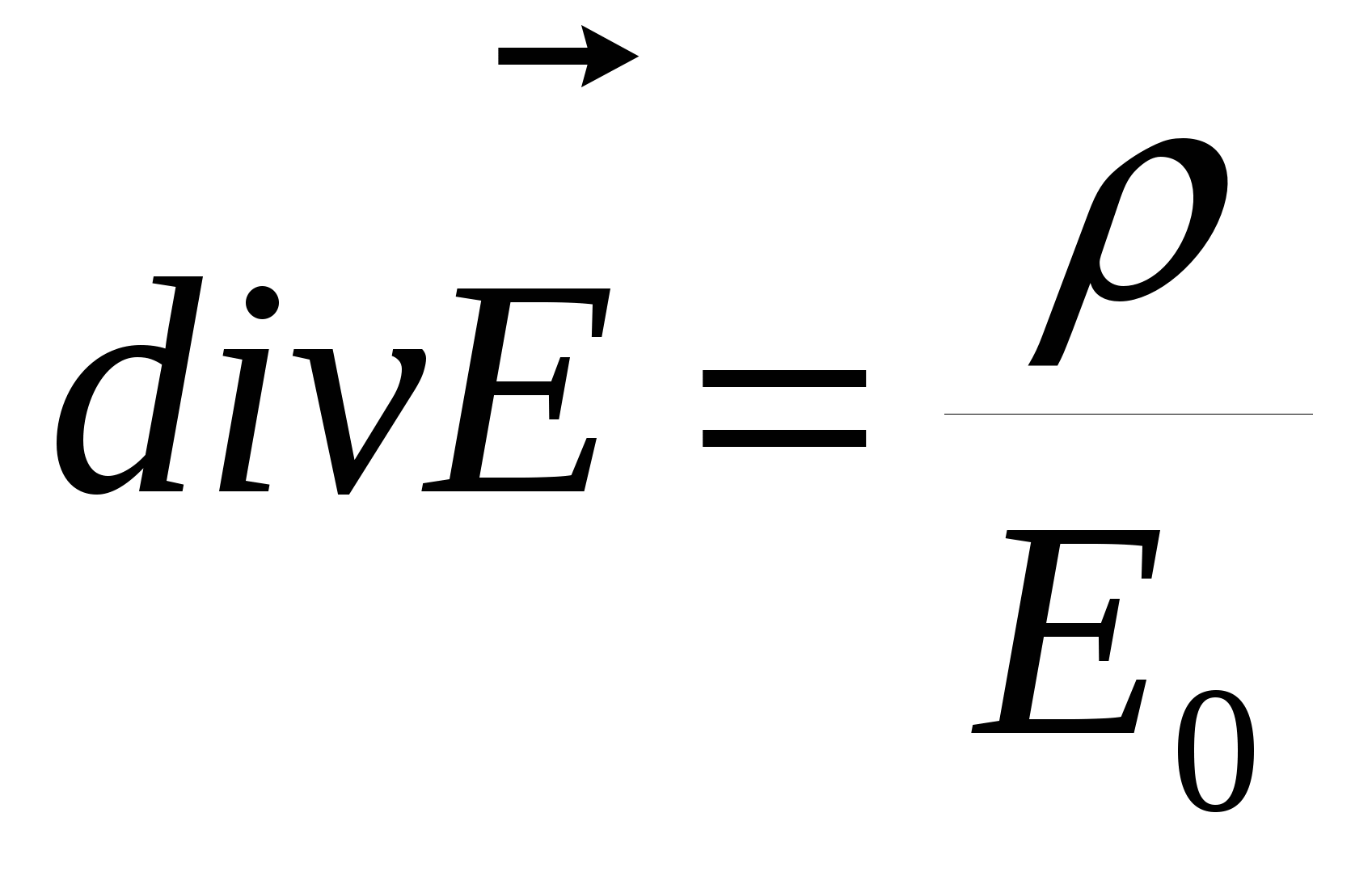
Из ТРЕТЬЕГО уравнения Максвелла следует, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле. По теореме Стокса в векторном анализе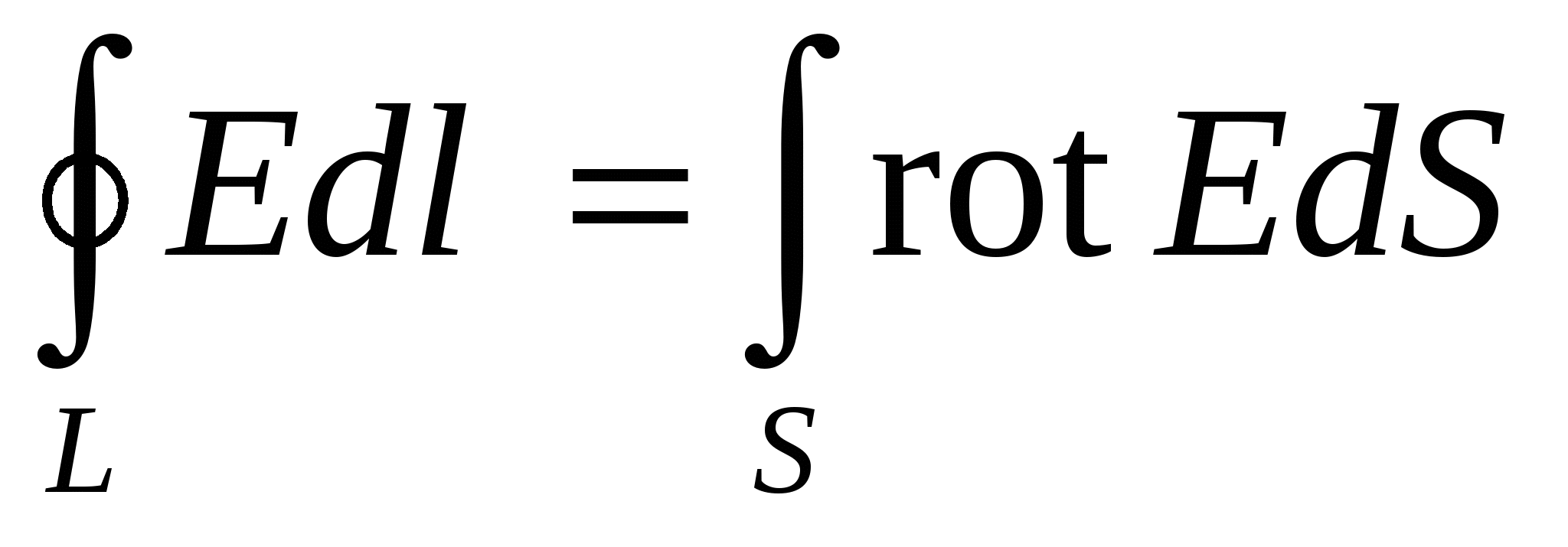 , где ротор вектора Е выражается определителем , где ротор вектора Е выражается определителем
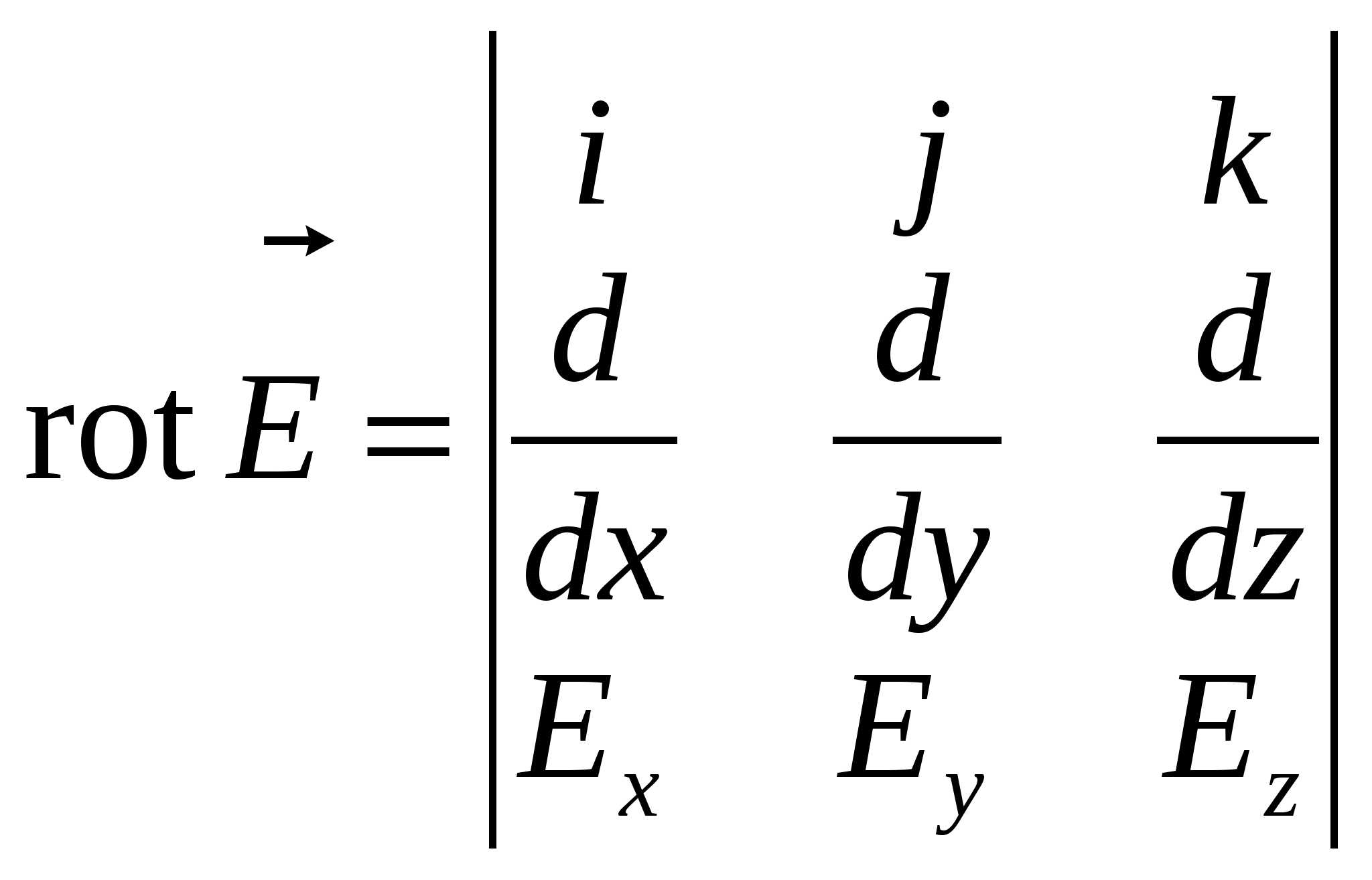
что позволяет записать первое уравнение Максвелла в дифференциальном виде
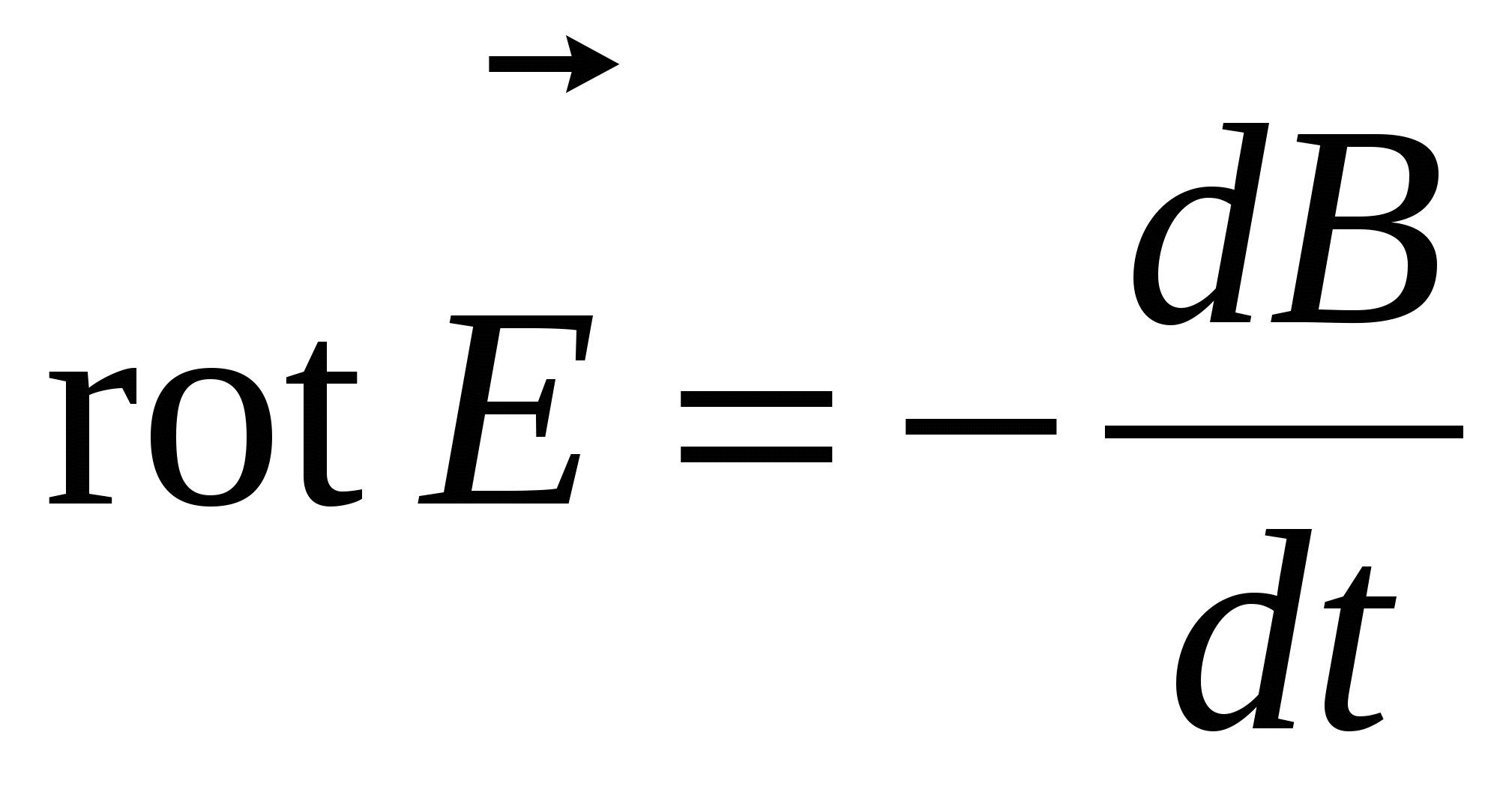
|
 Скачать 1.21 Mb.
Скачать 1.21 Mb.