Вопрос31. Движение заряженных частиц в магнитном поле. Сила Лоренца. Ускорители заряженных частиц.
СИЛА ЛОРЕНЦА
Сила, действующая на заряженные частицы, двигающиеся в магнитном поле, называется силой Лоренца: F=q[v(в), B(в)]; Сила Лоренца всегда перпендикулярна скорости и следовательно направлению перемещения, поэтому она работы не совершает. Сила Лоренца может изменять только направление движения частицы, но не может изменять ее кинетическую энергию. Если на движующуюся частицу действует не только магнитное поле, но и электрическое, то результирующую силу можно расчитать по формуле: F=qE(в)+q[U(в)B(в)] – обобщенная сила Лоренца.
На заряженную частицу в магнитном поле действует сила Лоренца
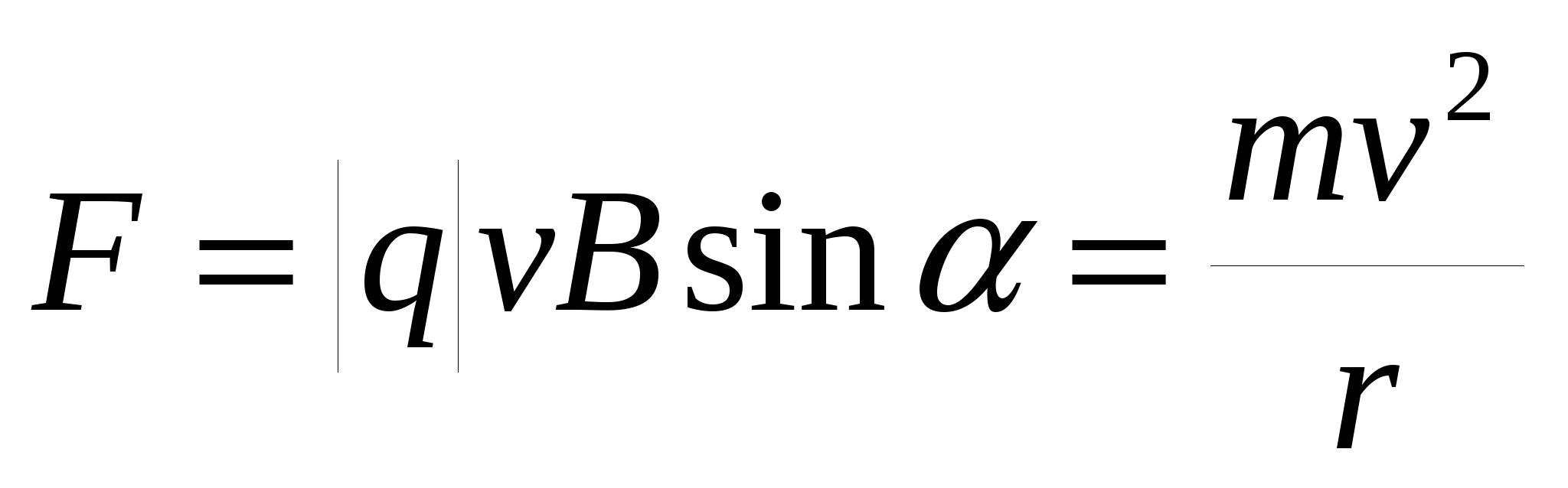
которая направлена перпендикулярно скорости частицы и сообщает нормальное ускорение.
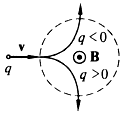
В однородном магнитном поле, направленном перпендикулярно скорости частицы, частица равномерно движется по окружности, плоскость которой перпендикулярно вектору В, а радиус равен
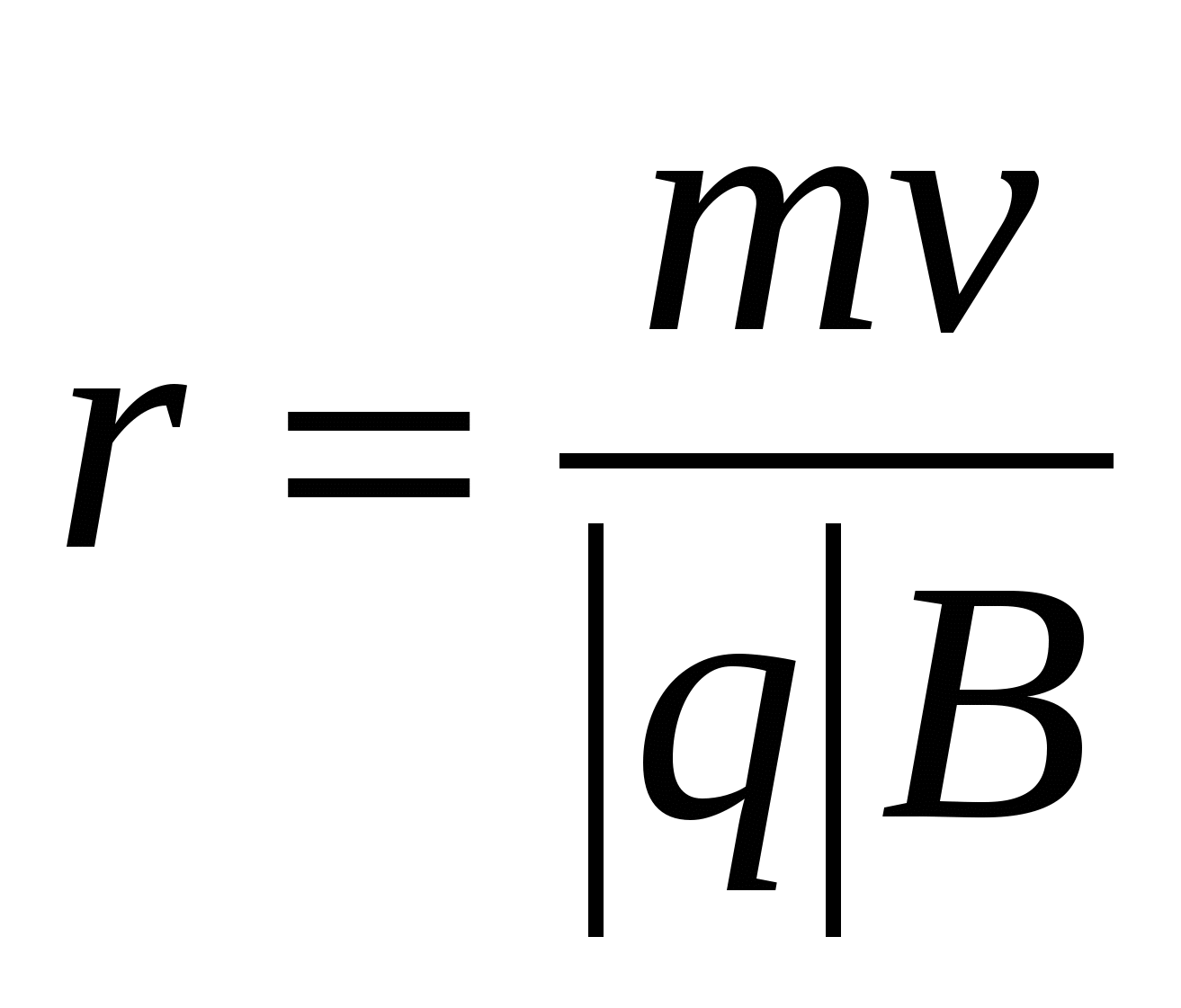
Период вращения заряженной частицы не зависит от ее скорости и равен
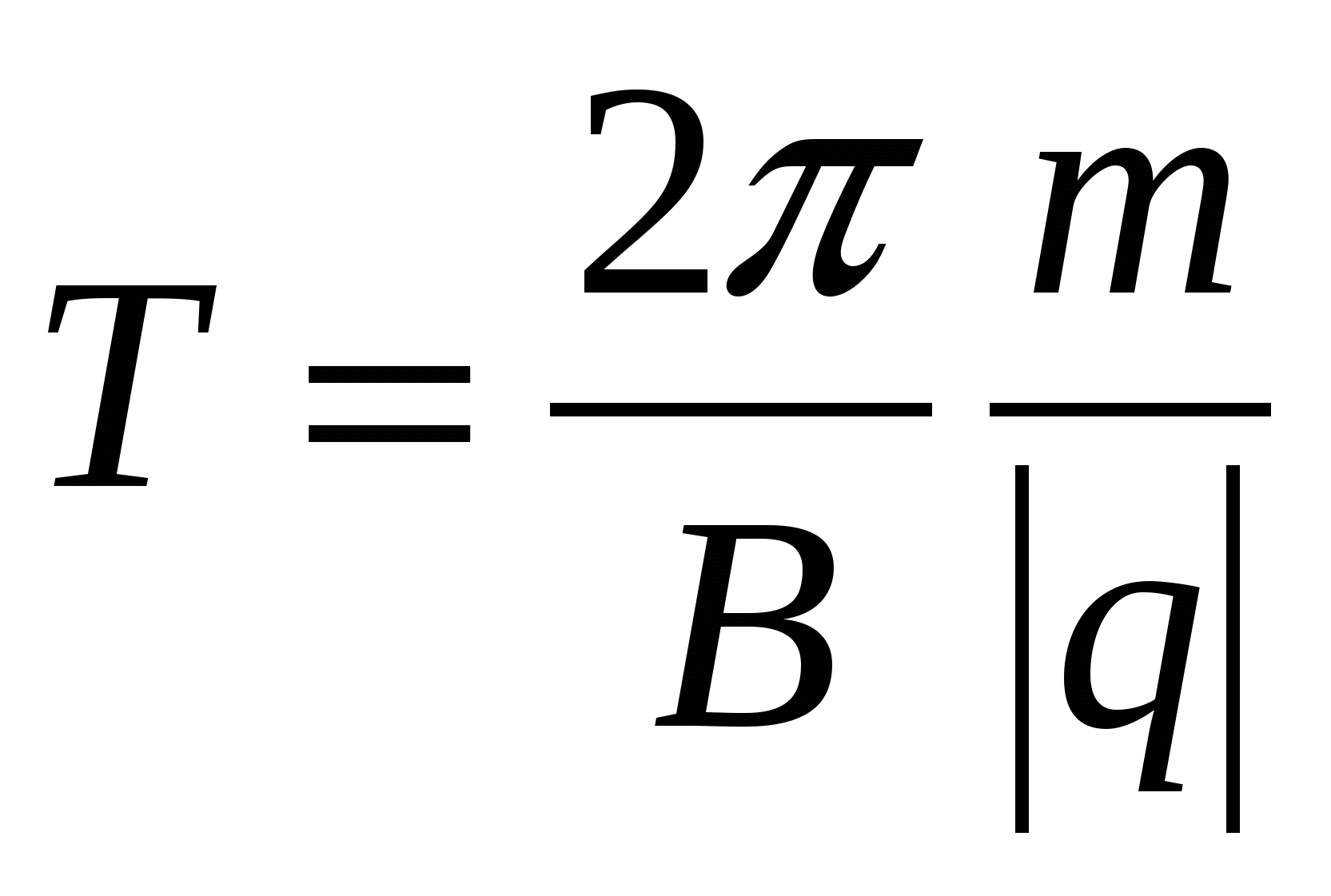
|
Вопрос32. Эффект Холла и его применение.
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов при помещении проводника с постоянным током в магнитное поле.
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течёт электрический ток под действием напряжённости E. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1 не скомпенсирует магнитную составляющую силы Лоренца:
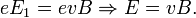
Скорость электронов v можно выразить через плотность тока:
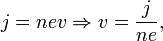
где n — концентрация носителей заряда. Тогда
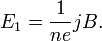
Коэффициент 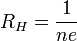 пропорциональности между E1 и jB называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как алюминий, цинк, железо, кобальт), в сильных полях наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твёрдого тела. пропорциональности между E1 и jB называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как алюминий, цинк, железо, кобальт), в сильных полях наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твёрдого тела.
Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле или полупроводнике, что делает его незаменимым методом исследования свойств полупроводников.
На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля.
|
Вопрос33. Явление электромагнитной индукции. Правило Ленца. Закон Фарадея-Ленца (основной закон электромагнитной индукции) и его вывод из закона сохранения энергии.
ЯВЛЕНИЕ ЭЛЕКТРО-МАГ. ИНДУКЦИИ. ПРАВИЛО ЛЕНЦА.
Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемой этим контуром возникает электрический ток, называемый индукционным потоком. Эксперементально установленно, что величина индукции тока не зависит от способов изменения магнитного потока, а определяет лишь скорость изменения. Индукционный ток в проводнике может возникнуть только под действием ЭДС. ЭДС, возникшая в проводнике при изменении магнитного потока, называется ЭДС-индукции. Согласно закону Фарадея: ε инд=k dФm/dt. Направление индукции тока определяется по правилу Ленца. При всяком изменении магнитного потока сквозь поверхность натянутую на замкнутый контур, в нем возникает индукционный ток такого направления, что его магнитное поле препятствует изменению магнитного потока. С учетом правила Ленца закон Фарадея имеет вид: ε инд = - dФm/dt; Поскольку для замкнутого контура dФm=dψ, то ε инд = - dψ/dt
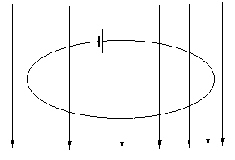
Рассмотрим замкнутый проводящий контур в неоднородном магнитном поле. Если этот контур включить в цепь гальванического элемента, то он придет в движение. Элементарная работа за время dt по перемещению контура будет равна
dA1 = I dФ. Работа, совершаемая током при прохождении по проводнику, определяется законом Джоуля - Ленца dA2 = I2 R dt. Полная работа, совершаемая за это время гальваническим элементом, равна
dA = I dt, где - ЭДС источника тока. В соответствии с законом сохранения энергии: dA = dA1 + dA2, то есть I dt = I dФ + I2 R dt.
Отсюда I = ( dt - dФ) / R dt = (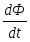 R = (+и) / R, тогда и= R = (+и) / R, тогда и= 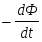 . .
|
Вопрос34. Явление самоиндукции. Индуктивность. Электродвижущая сила самоиндукции. Индуктивность соленоида.
Электрический ток, текущий в замкнутом контуре создает вокруг себя магнитное поле, индукция которого по закону Био-савара-Лапласа пропорциональна току, поэтому сцепленный с контуром магнитный поток будет также пропорционален току в этом контуре. Коэффициентом пропорциональности является величина L – индуктивность.Фm=LI; L=Фm/I
Если ток в контуре будет изменяться, то будет изменяться и сцепленный с контуром магнитный поток, поэтому в нем будет ЭДС, возникновение ЭДС индукции в проводящем контуре при изменении силы тока в нем называется самоиндукцией. ε инд = - dФm/dt= - (L[dI/dt]+J[dl/dt]); L зависит от формы проводника и магнитной проницаемости среды, в которой он находится. Обычно величина L не зависит от силы тока в контуре, поэтому L=const, поэтому ε инд= - L (dI/dt)
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.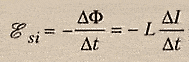
ИНДУКТИВНОСТЬ БЕСКОНЕЧНО ДЛИННОГО СОЛИНОЙДА.
Найдем индуктивность магнитного поля внутри солинойда.
Замкнутый ∫[по L]B(в)dl(в)=μ0 ΣIab;
Замкнутый ∫ [по L] B(в)dl(в)=∫[по AB]B(в)dl(в)+
+∫[по CB]B(в)dl(в) + ∫[CD]B(в)dl(в)+∫[по DA]B(в)dl(в); Интеграл по участку AB равен нулю, т.к. вне солинойда поле практически отсутствует.
Интегралы по участку CD и DA равны по величине и противоположны по знаку => их сумма равна нулю; Замкнутый ∫B(в)dl(в)=∫[по CD]B(в)dl(в).
B и dl совпадают по направлению и кроме этого внутри солинойда B=const (т.к. солинойд бесконечно длинный). Если длина CD=ЭЛ, то замкнутый ∫B(в)dl(в)=Bl=μ0 N J; N – число витков, охватывающих контур. B=μ0 N I / l;
Ф1=BS, S – площадь поперечного сечения солинойда; ψ=NФ1=NBS – магнитный поток; ψ=N S μ0 μ (N/l) I=μ0μ (N(c.2)/ l )SI; L=μ0 μ (N^2 ) V;
|
Вопрос 35. Токи при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т.е. направлены противоположно току, создаваемую источником. При выключение источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
1). Рассмотрим процесс выключения тока в цепи, содержащей источник тока с ЭДС, резистор сопротивления и катушку индуктивностью.
В момент времени отключим источник тока. Ток в катушке индуктивностью начнет уменьшаться, что приведет к возникновению ЭДС самоиндукции, препятствующей, согласно правилу Ленца, уменьшению тока.
Оценим значение ЭДС самоиндукции, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от 1 до 2. Предположим, что мы размыкаем контур, когда в нем течет установившейся ток.
Т.е. при значительном увеличении сопротивления цепи, обладающей большой индуктивностью, ЭДС самоиндукции может во многом раз превышать ЭДС источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это может привести к пробою изоляции и выводу из строя измерительных приборов.
2). При замыкании цепи помимо внешней ЭДС возникает ЭДС самоиндукции, препятствующая, согласно правилу Ленца, возрастанию тока.
Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности называются взаимной индуктивностью контуров.
|
Вопрос36. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
Рассмотрим контур индуктивностью L по которому течек ток I. С данным контуром сцеплен магнитный поток Ф=LI. При изменении тока в контуре на dI, dФ=LdI. При этом совершается работа dA.
Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
П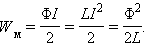 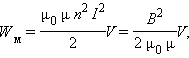 рименим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить: рименим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле.
Ф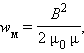 изическая величина (см. рис3.) изическая величина (см. рис3.)
равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.
| |
 Скачать 1.21 Mb.
Скачать 1.21 Mb.