Решение По условию задачи начальная скорость частицы где i,j, орты единичных векторов и тогда модуль начальной скорости
 Скачать 379.86 Kb. Скачать 379.86 Kb.
|
|
Вариант 12 1.12.Скорость частицы зависит от времени по закону 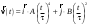 . Через сколько секунд ускорение частицы будет направлено под углом 45 к оси y, если . Через сколько секунд ускорение частицы будет направлено под углом 45 к оси y, если 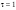 с, А = В = 1 м/c? с, А = В = 1 м/c?
Ускорение – производная скорости по времени 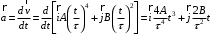 Тангенс угла 450 выразим как 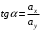 , где , где 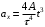 и и 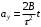 , тогда , тогда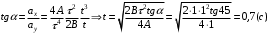 Ответ: t=0,7 с 2-12. Частица начала свое движение из начала координат с начальной скоростью 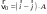 и с ускорением, которое зависит от времени по закону а) и с ускорением, которое зависит от времени по закону а) 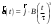 , б) , б) 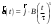 , в) , в) 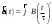 . Каков модуль скорости частицы в момент времени . Каков модуль скорости частицы в момент времени 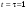 с, если А = 1 м/с, В =1 м/с2. с, если А = 1 м/с, В =1 м/с2.
По условию задачи начальная скорость частицы 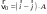 где i,j, – орты единичных векторов и 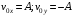 тогда модуль начальной скорости 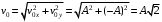 По условию ускорение зависит по времени 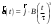 т.е. 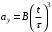 и модуль ускорения и модуль ускорения 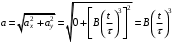 По определению конечная скорость равна 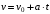 Отсюда получаем 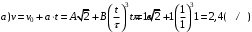 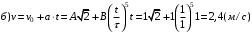 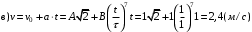 Ответ: а)2,4 м/с; б)2,4 м/с; в)2,4 м/с 3 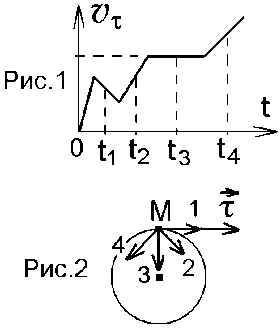 -12э. Материальная точка M движется по окружности со скоростью -12э. Материальная точка M движется по окружности со скоростью  . На рис.1 показан график зависимости проекции скорости . На рис.1 показан график зависимости проекции скорости 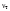 на орт на орт 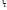 , направленный вдоль скорости , направленный вдоль скорости 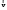 . На рис.2 укажите направление силы, действующей на точку M в момент времени t1: . На рис.2 укажите направление силы, действующей на точку M в момент времени t1:а) 1 б) 2 в) 3 г) 4 Решение: Из графика видно, что проекция скорости vz в момент времени t1 уменьшается, движение точки является равнозамедленным, т.к. участок графика – прямая линия. Тангенциальное ускорение характеризует быстроту изменения скорости по модулю, следовательно, величина тангенциального ускорения не изменяется, вектор тангенциального ускорения направлен против τ. Нормальное ускорение всегда направлено к центру окружности, тогда модуль полного ускорения определяется как 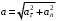 и будет направлен под углом φ к направлению нормального ускорения (см рисунок) и будет направлен под углом φ к направлению нормального ускорения (см рисунок) По второму закону Ньютона сила равна 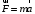 , т.е. имеет такое же направление, как и полное ускорение точки, тогда получаем, что сила в точке М имеет направление 3. , т.е. имеет такое же направление, как и полное ускорение точки, тогда получаем, что сила в точке М имеет направление 3.Ответ: в) 3 4 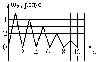 -12э. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным? -12э. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?а) 10 с; б) 1 с; в) 2 с; г) 9 с Решение: По определению 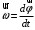 . Отсюда . Отсюда 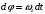 и и 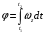 . Используя геометрический смысл интеграла, искомый угол можно найти как площадь фигуры, ограниченной кривой линией. Наибольшая площадь будет ограничена линией над осью времени, т.е. угол поворота тела относительно начального положения будет максимальным в момент времени, равный 2 с . Используя геометрический смысл интеграла, искомый угол можно найти как площадь фигуры, ограниченной кривой линией. Наибольшая площадь будет ограничена линией над осью времени, т.е. угол поворота тела относительно начального положения будет максимальным в момент времени, равный 2 сОтвет: в) 2 с. 5-12э. Теннисный мяч летел с импульсом 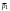 (масштаб и направление указаны на рисунке). В перпендикулярном направлении на короткое время (масштаб и направление указаны на рисунке). В перпендикулярном направлении на короткое время 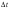 = 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40 Н. Какова стала величина импульса p2 после того, как ветер утих? = 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40 Н. Какова стала величина импульса p2 после того, как ветер утих?а) 5 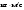 б) 0,5 б) 0,5 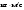 в) 43 в) 43 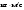 г) 50 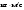 д) 7 д) 7 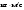
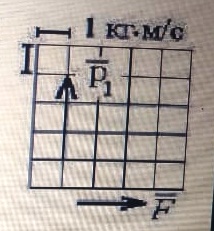 По условию задачи F=const, тогда воспользуемся законом импульса силы в виде: 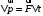 отсюда получаем, что отсюда получаем, что 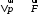 . . в скалярном виде получим изменение импульса мяча 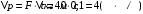 Построим треугольник импульсов: 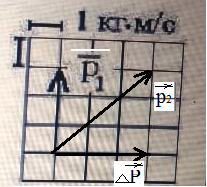 По теореме Пифагора найдем модуль р2 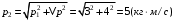 Ответ: а) 5 кг·м/с 6-12. Тело вращается вокруг закрепленной оси с угловой скоростью, зависимость от времени которой задается графиком. Момент инерции тела относительно оси вращения равен I. Найти а) отношение модулей моментов сил; б) на сколько отличаются модули моментов сил, действующих на тело в моменты времени 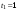 с и с и 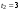 с. с. 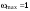 с–1, I = 1 с–1, I = 1 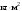
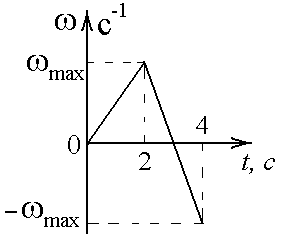 Из второго закона Ньютона, применяемого к вращающимся телам, момент сил определяется формулой 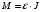 , где ɛ - угловое ускорение, которое определяется из кинематического уравнения , где ɛ - угловое ускорение, которое определяется из кинематического уравнения 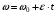 Как видим из графика, начальная угловая скорость равна 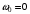 тогда угловое ускорение тогда угловое ускорение 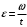 , тогда момент сил , тогда момент сил 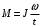 Отношение моментов сил 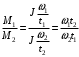 В моменты времени t1=1 c и t2=3 c отношение модулей моментов сил будет равно 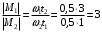 Ответ: отличаются в 3 раза. 7-12. Перпендикулярно однородному тонкому стержню массы m= 1 кги длиной l= 1 мпроходят две параллельные оси. Одна проходит через центр масс стержня С, а другая через точку О, лежащую на расстоянии х = 0,4 м от его конца А. На сколько отличаются моменты инерции стержня относительно этих осей?
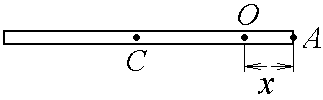 По теореме Штейнера момент инерции стержня 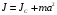 , где , где 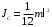 - момент инерции стержня относительно оси, проходящей через середину стержня; а – расстояние от середины стержня до оси вращения, в нашем случае - момент инерции стержня относительно оси, проходящей через середину стержня; а – расстояние от середины стержня до оси вращения, в нашем случае 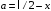 Тогда момент инерции стержня относительно т.O будет равен 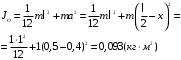 Тогда момент инерции стержня относительно т.С будет равен 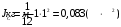 Отсюда 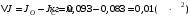 Ответ: 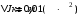 8-12. Тело движется вдоль горизонтальной оси х под действием силы 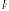 , направленной под углом к оси х. В некоторый момент тело достигает скорости , направленной под углом к оси х. В некоторый момент тело достигает скорости 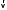 , а мощность силы равна N. Найдите а) косинус угла ; б) синус угла . , а мощность силы равна N. Найдите а) косинус угла ; б) синус угла .F = 1 Н, 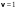 м/с, N= 0,5 Вт. м/с, N= 0,5 Вт.
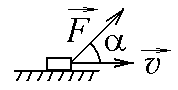 Мощность по определению равна 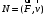 Если вектор силы направлен под углом, то 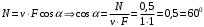 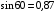 Ответ: 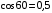 ; ; 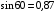 9.12. Небольшая тележка описывает «мертвую петлю» радиусом 2 м, скатываясь с минимальной высоты, обеспечивающей прохождение мертвой петли тележки. На какой высоте от нижней точки петли сила давления тележки на рельсы равна 3/2 силы тяжести тележки. Трением пренебречь.
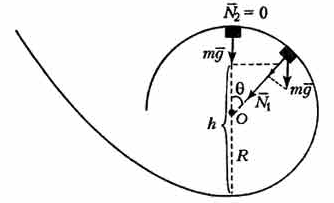 При минимальной энергии, обеспечивающей прохождение всей петли, сила нормальной реакции в верхней точке обращается в ноль. Сначала определим минимально необходимую высоту для того, чтобы тележка прошла петлю. Условием прохождения петли является ненулевая сила реакции опоры во всех точках петли, кроме самой верхней. Для этой верхней точки составляем второй закон Ньютона: 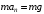 Или 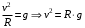 Теперь, когда мы знаем необходимую минимальную скорость в вершине петли  , составим закон сохранения энергии: , составим закон сохранения энергии: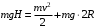 Откуда 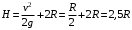 Теперь рассмотрим точку, в которой сила давления на рельсы равна 1,5 силы тяжести тележки. Составим для нее второй закон Ньютона в проекциях на радиальную ось: 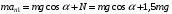 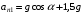 Скорость в этой точке 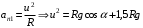 Составим для этой точки закон сохранения энергии: 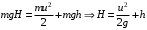 Подставим сюда найденную высоту Н и выразим искомую величину 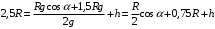 , где , где 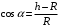 тогда 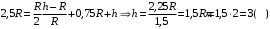 Ответ: h=3 м. 10.12. На наклонной плоскости, синус угла наклона которой к горизонту 0,28, на высоте 2,1 м лежит шайба. Коэффициент трения шайбы о плоскость 0,5. Какую скорость надо сообщить шайбе вниз по наклонной плоскости, чтобы после абсолютно упругого удара об упор, находящийся у основания плоскости, шайба вернулась в исходную точку?g=9,8 м/с2
Для решения задачи применим закон сохранения энергии: 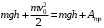 (1) (1)Здесь Атр – это часть механической энергии перешедшая при движении шайбы вниз и обратно во внутреннюю энергию при ударе шайбы об упор. Вычислим работу сил трения. 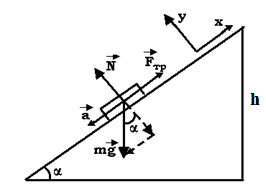 Условие, при котором тело будет двигаться вниз, определим через второй закон Ньютона: 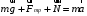 Проекция на ось ох: 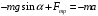 (1) (1)Проекция на ось оу: 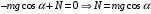 (2) (2)По определению сила трения 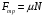 , учитывая (2) получим , учитывая (2) получим 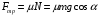 Тогда работа сил трения будет равна 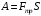 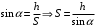 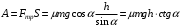 При движении вверх работа силы трения будет такой же, поэтому общая работа 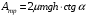 По условию 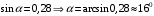 Из (1) выразим скорость скольжения шайбы 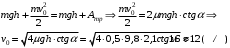 Ответ: v0=12 м/с. |

 - ?
- ?