Ответы информатика(1). Закон (теорема) сложения вероятностей
 Скачать 2.08 Mb.
|
|
Н1: F(x) 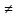 Fтеор(х).Задается уровень значимости, например, α≤0,05. Если хотим проверить, согласуются эмпирические данные с нашим гипотетическим предложением относительно теоретической функции распределения или нет, то используем критерий согласия. Критерий согласия– это критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Рассмотрим один из них, использующий Х2 распределение и получивший название критерий согласия Пирсона. Этот критерий не требует никаких пердположений о параметрах совокупности, из которых извлечена выборка. Это непараметрический критерий. Применим критерий Х2 (хи-квадрат) к проверке нулевой гипотезы Н0, что генеральная совокупность распределена по нормальному закону. Критерий предполагает, что результаты наблюдений группированы в вариационный ряд и разбиты на классы. По выборке объема n построим эмпирическое распределение Fэмп(х): варианты х1, х2, …, хn эмпирические частоты n1, n2, …, nn и сравним его с предполагаемым теоретическим распределением, вычисленным в предположении нормального закона распределения. Теоретические частоты: n1’, n2’, …, nn’/ То есть фактически Н0: nэмп=nтеор’. В качестве критерия проверки нулевой гипотезы примем случайную величину: 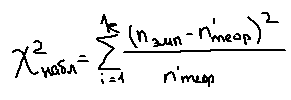 ,где k – число классов. Из таблиц находим Хкрит2(α≤0,05, f=k-3). Сравниваем, если Хнабл2<Хкрит2(α, f) => Н0 – данное распределение подчиняется нормальному закону. Если наоборот, то не подчиняется нормальному закону. 10. Функциональная и корреляционная зависимости. Коэффициент линейной корреляции и его свойства. Функциональная зависимость – это зависимость вида y=f(x), когда каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y. Корреляционная зависимость – это статистическая зависимость, проявляющаяся в том, что при изменении одной из величин изменяется среднее значение другой: 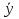 =f(x).Для изучения корреляционной связи данные о статистической зависимости удобно задавать в виде корреляционной таблицы или в виде двумерной выборки.
Схема эксперимента следующая: пусть имеется выборка объема n из генеральной совокупности N. На каждом объекте выборки определяют числовые значения признаков, между которыми требуется установить наличие или отсутствие связи. Таким образом, получаем 2 ряда числовых значений. Для наглядности полученного материала каждую пару можно представить в виде точки на координатной плоскости. По оси абсцисс откладывают значения одного вариационного ряда – xi, а по оси ординат – другого – yi. Такое изображение статистической зависимости называется полем корреляции, или корреляционным полем точек. Оно создает общую картину корреляции. 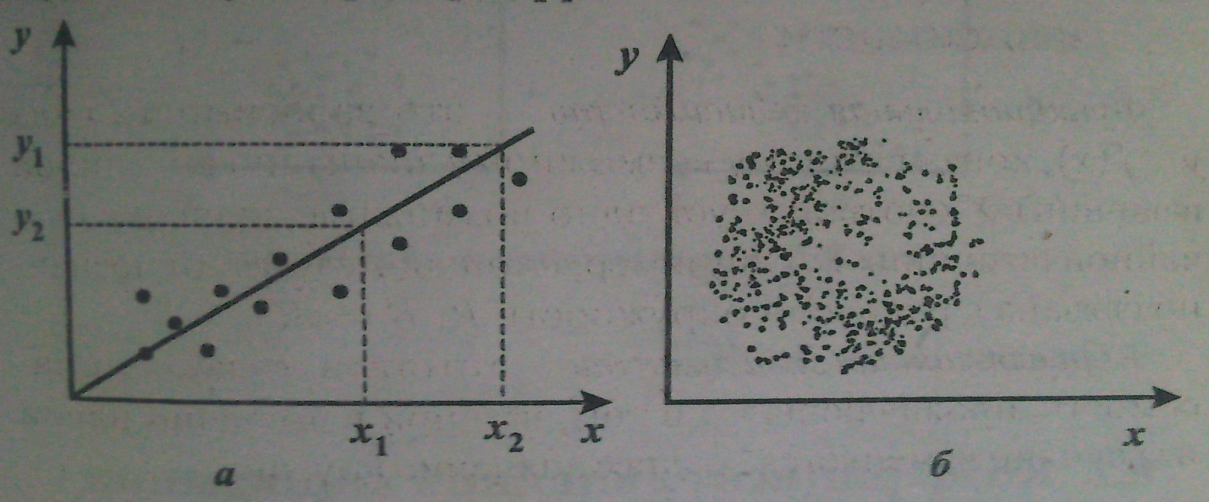 А) точки сгруппированы вдоль некоторого направления, это говорит о наличии линейной корреляционной связи между признаками. Б) точки распределены неравномерно , это говорит о том, что линейная корреляция отсутствует На практике исследователя часто может интересовать не сама зависимость одной переменной от другой, а именно характеристика тесноты связи между ними, которую можно было бы выразить одним числом. Эта характеристика называется выборочным коэффициентом линейной корреляции r. Требования к корреляционному анализу: корреляционный анализ – это метод, используемый, когда данные можно считать случайными и выбранными из совокупностей, распределенных по нормальному закону. Выборочный коэффициент линейной корреляции r характеризует тесноту линейной связи между количественными признаками в выборке: 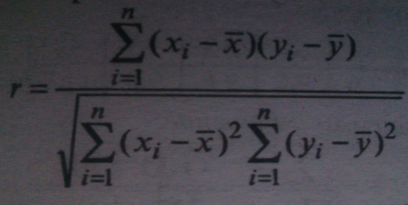 Если r>0, то корреляционная связь между переменными прямая, при r<0 – связь обратная. СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ r: Они проявляются при достаточно большом объеме выборки n.
r<0.3 – слабая связь r=0,3 – 0,5 – умеренная связь r=0,5 – 0,7 – заметная(значительная) r=0,7 – 0,8 – достаточно тесная r=0,8 – 0,9 – тесная(сильная) r> 0,9 – очень сильная
x и y могут взаимозаменяться, не влияя на величину r.
11.Ошибка выборочного коэффициента линейной корреляции. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции. это ответ на вопрос существует ли вообще эта связь. Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра. Выборочный коэффициент линейной корреляции rв – величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина имеет ошибку mr. Чтобы выяснить находятся ли случайные величины X и Y генеральной совокупности в линейной корреляционной зависимости, надо проверить значимость rв Для этого проверяют нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности Н: rген = 0, то есть линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза Н1: rген ≠ 0. ,т.е. эта линейная корреляционная связь имеется. Задаётся уровень значимости, например, α≤0,05 Критерием для проверки нулевой гипотезы является отношение выборочного коэффициента корреляции к своей ошибке: 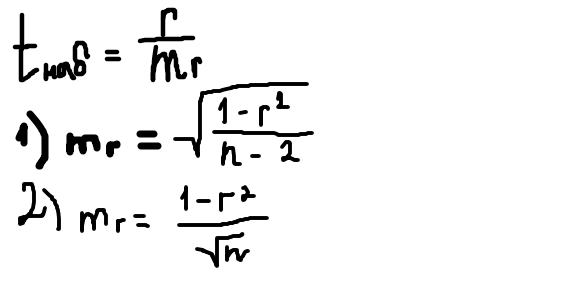 где mr – ошибка коэффициента корреляции. Если объем выборки n<100, то mr = формуле (1), если n>100, то формуле (2). Число степеней свободы проверки критерия равно f=n-2. Гипотезу проверяют по таблицам распределения Стьюдента в соответствии с выбранным уровнем значимости. По таблице критических точек распределения Стьюдента находим tкрит (α,f), определённое на уровне значимости α≤0,05 при числе степеней свободы f=n-2, где n – объём двумерной выборки.Если tнабл>tкрит →Н1 – отвергают нулевую гипотезу и принимают альтернативную: : rген ≠ 0, имеется линейная корреляционная связь между признаками. Если tнабл 12. Выборочное уравнение линейной регрессии. Нелинейная регрессия. Коэффициент корреляции рангов Спирмена. Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватнойдля описания имеющихся данных. Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных. Регрессия – это функция, позволяющая по величине одного признака Х находить среднее ожидаемое (должное) значение другого признака Y, корреляционно связанного с Х. В линейной математической модели уравнение линейной регрессии имеет вид: 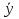=ax+b,где a и b – параметры линейной регрессии Если график регрессии 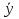=f(х) изображается кривой, то это не линейная регрессия.Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, литературных источников, профессионального мнения и визуального наблюдения расположения точек корреляционного поля. Этот очень важный этап анализа называется спецификацией. Для определения неизвестных параметров регрессии используется метод наименьших квадратов. Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле:.  где  - сумма квадратов разностей рангов, а - число парных наблюдений. При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи. 13. Определение дисперсионного анализа (ДА). Основные понятия и виды ДА. ДА – статистический метод анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, основанный на сравнении оценок дисперсий соответствующих групп выборочных данных. фактор – различные, независимые, качественные показатели, влияющие на изучаемые признаки. Обозначаются факторы А,В,С… факторы, контролируемые и измеряемые в процессе исследования называются регулируемыми. Признаки, изменяющиеся под воздействием тех или иных факторов, называют результативными. Для их обозначения используют X, Y, Z. Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии, определяемой влиянием регулируемого фактора и остаточной дисперсии, обусловленной действием неконтролируемых и случайных причин. С помощью F-критерия устанавливается влияние фактора на признак. 14. Условия проведения дисперсионного анализа (ДА). Однофакторный ДА. Условия применения дисперсионного анализа к выборочным данным:
Схема проведения однофакторного дисперсионного анализа:
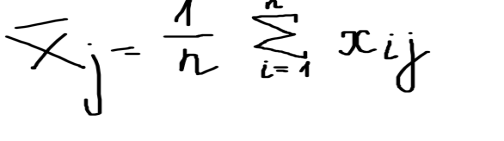 и общее выборочное среднее, где N= n*m :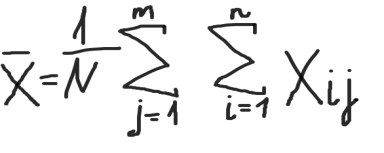 
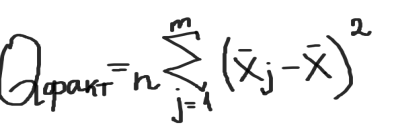 определяется внутригрупповая сумма квадратов, которая показывает отклонение наблюдений хij от соответствующих групповых средних хj и учитывает разбросы значений хij внутри каждой из групп, вызванные случайными признаками при постоянном значении фактора А: 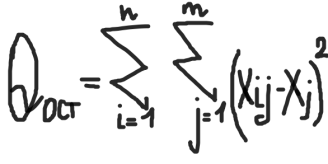 Общая сумма квадратов: 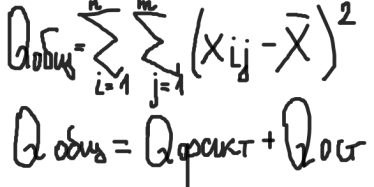 Определение числа степеней свободы для факторного отклонения: fфакт= m-1, для остаточной вариации: fост= N-m, для общего: fобщ= N-1 или fобщ=fфакт+fост Факторная выборочная дисперсия: 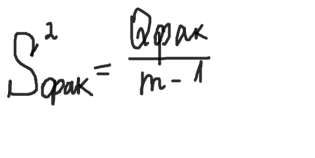 Остаточная выборочная дисперсия: 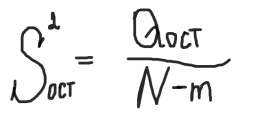 Общая дисперсия: 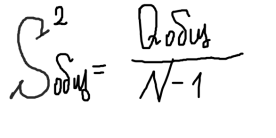 6) определяется эффективность влияния фактора А на результативный признак. Для этого сравнивают расчетный критерий фишера и его табличное значение. Влияние фактора А считается значимым на уровне значимости α, если выполняется неравенство: 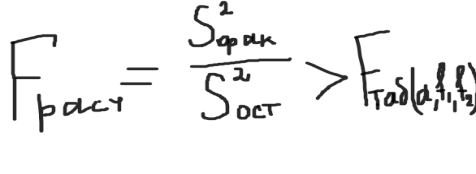 Значение Fтабл(α,f1,f2) находится по таблице для заданного уровня значимости. Если неравенство не выполняется, то влияние фактора А на результативный признак считается несущественным. 15. Анализ двухфакторных комплексов. Понятие о многофакторном комплексе. Влияние 2ух факторов А и В одновременно действующие на признак х. Последовательность этапов двухфакторного анализааналогично схеме однофакторного анализа. Однако в этом анализе необходимо кроме оценки влияния каждого фактора учитывать их совместное действие на результативный признак.Он проводится по схеме:
- вычисляются групповые выборочные средние при постоянном значении фактора А - групповые выборочные значения при постоянном значении фактора В - общее выборочное среднее 3) Расчитываются межгрупповые суммы квадратов отклонений - для фактора А -для фактора В -для совместного действия факторов А и В - внутригрупповая сумма квадратов отклонений для прочих факторов (Qост) -общая сумма квадратов отклонений 4) Нахождение числа степеней свободы (для влияния фактора А, В, для совместного влияния факторов А и В,для прочих факторов(Qост) и для общего варьирования(Qобщ)) 5) Определяются выборочные дисперсии как отношение сумм квадратовотклонений к соответствующим числам степеней свободы  6) Определяется значимость влияния фактора А,В и их совместного действия на результативный признак. Для этого расчетное значение критерия Фишера сравнивается с его табличной величиной. Влияние фактора А считается значимым на уровне значимости α, если выполняется неравенство:  Значение Fтабл(α, f1, f2) находится по таблице фишера-снедекора для заданного значения уровня значимости α и числа степеней свободы f1 и f2. Если какое-либо неравенство не выполняется, то влияние фактора на результативный признак считается несущественным. |