Ответы информатика(1). Закон (теорема) сложения вероятностей
 Скачать 2.08 Mb. Скачать 2.08 Mb.
|
|
1. Случайное событие. Вероятность случайного события. Классическое и статистическое определение вероятности. Понятие о совместных и несовместных событиях. Закон (теорема) сложения вероятностей. Случайное событие – это любой факт, который в результате испытания может произойти или не произойти. Случайное событие – это результат испытания. Испытание – это эксперимент, выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. События обозначаются заглавными буквами латинского алфавита А,В,С. Численная мера степени объективности возможности наступления события называется вероятностью случайного события. Классическое определение вероятности события А: Р(А)=m/n Вероятность события А равна отношению числа случаев, благоприятствующих событию A(m), к общему числу случаев (n). Статистическое определение вероятности Относительная частота событий – это доля тех фактически проведенных испытаний, в которых событие А появилось W=P*(A)= m/n. Это опытная экспериментальная характеристика, где m – число опытов, в которых появилось событие А; n – число всех проведенных опытов. Вероятностью события называется число, около которого группируются значения частоты данного события в различных сериях большого числа испытаний P(A)= 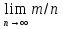 . .События называются несовместными, если наступление одного из них исключает появление другого. В противном случае события – совместные. Сумма двух событий – это такое событие, при котором появляется хотя бы одно из этих событий (А или В). Если А и В совместные события, то их сумма А+В обозначает наступление события А или события В, или обоих событий вместе. Если А и В несовместные события, то сумма А+В означает наступление или события А или события В. 2. Понятие о зависимых и независимых событиях. Условная вероятность, закон (теорема) умножения вероятностей. Формула Байеса. Событие В называется независимым от события А, если появление события А не изменяет вероятности появления события В. Вероятностью появления нескольких независимых событий равна произведению вероятностей этих: P(AB) = P(A)*P(B) Для зависимых событий: P(AB) = P(A)*Р(B/A). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло. Условная вероятность события В - это вероятность события В, найденная при условии, что событие А произошло. Обозначается Р(В/А) Произведение двух событий – это событие, состоящее в совместном появлении этих событий (А и В) Формула Байеса служит для переоценки случайных событий P(H/A) = (P(H)*P(A/H))/P(A) P(H) – априорная вероятность события Н P(H/A) – апостериорная вероятность гипотезы H при условии, что событие А уже произошло P(A/H) – экспертная оценка P(A) – полня вероятность события А 3. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. Нормальный закон распределения непрерывных случайных величин. Случайная величина – это величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений. Дискретная случайная величина – это случайная величина, когда принимает отдельное изолированное, счетное множество значений. Непрерывная случайная величина – это случайная величина, принимающая любые значения из некоторого интервала. Понятие непрерывной случайной величины возникает при измерениях. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Таблица – это простейшая форма задания закона распределения
Требования: Аналитический: 1)F(x)=P(X Функция распределения = интегральная функция распределения. Для дискретный и непрерывных случайных величин. 2)f(x) = F’(x) Плотность распределения вероятностей = дифференциальная функция распределения только для непрерывной случайной велечины. Графический: 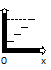 С-ва: 1) 0≤F(x)≤1 С-ва: 1) 0≤F(x)≤12) неубывающая для дискретных случайных величин 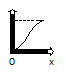 для непрерывных случайных величин для непрерывных случайных величин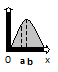 С-ва: 1) f(x)≥0 P(x)= С-ва: 1) f(x)≥0 P(x)=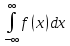 2) площадь S=1 для непрерывных случайных величин Характеристики: 1.математическое ожидание – среднее наиболее вероятное событие 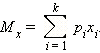 Для дискретных случайных величин. 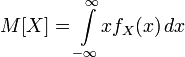 Для непрерывных случайных величин. 2)Дисперсия – рассеяние вокруг математического ожидания Для дискретных случайных величин: D(x)= 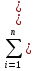 xi-M(x))2*pi xi-M(x))2*piДля непрерывных случайных величин: D(x)= 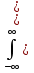 x-M(x))2*f(x)dx x-M(x))2*f(x)dx3)Среднее квадратическое отклонение: σ(х)=√(D(x)) σ – стандартное отклонение или стандарт х – арифметическое значение корня квадратного из ее дисперсии Нормальный закон распределения (НЗР) – закон Гаусса НЗР – это распад вероятностей непрерывной случайной величины, который описывается дифференциальной функцией 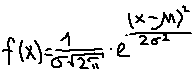 4. Основные понятия математической статистики. Генеральная совокупность и выборка. Статистическое распределение (вариационный ряд). Гистограмма. Полигон частот. Математическая статистика– это раздел математики, изучающий приближенные методы отыскания законов распределения и числовых характеристик по результатам эксперимента. Генеральная совокупность– это множество всех мыслимых значений наблюдений (объектов), однородных относительно некоторого признака, которые смогли быть сделаны. Выборка – это совокупность случайно отобранных наблюдений (объектов) для непосредственного изучения из генеральной совокупности. Статистическое распределение– это совокупность вариант xi и соответствующих им частот ni. Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных га оной прямой, основания которых одинаковы и равны ширине класса, а высота равна или частоте попадания в интервал ni или относительной частоте ni/n. Ширину интервала i можно определить по формуле Стерджеса: I=(xmax-xmin)/(1+3,32lgn), Где xmax – максимальное; xmin – минимальное значение вариант, а их разность носит название вариационный размах; n – объем выборки. 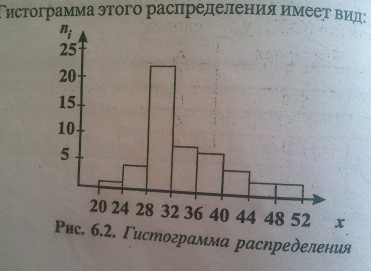 Полигон частот– ломаная линия, отрезки которой соединяют точки с координатами xi, ni. 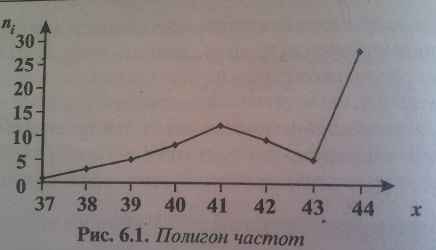 5. Характеристики положения (мода, медиана, выборочное среднее) и рассеяния (выборочная дисперсия и выборочное среднее квадратическое отклонение). Мода (Мо) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости. Для одномодальных распределений мода – это наиболее часто встречающаяся варианта в данной совокупности. Для определения моды интервальных рядов служит формула: M0=xниж+i*((n2-n1)/(2n2-n1+n3)), где хниж – нижняя граница модального класса, т.е. класса с наибольшей частотой встречаемости n2; n2 – частота модального класса; n1 – частота класса, предшествующего модальному; n3 – частота класса, следующего за модальным; i – ширина классового интервала. Медиана (Ме)-это значение признака. Относительно которого ряд распределения делится на 2 равные по объему части. Выборочная средняя– это среднее арифметическое значение вариант статистического ряда Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения: 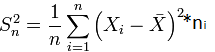 Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии: Sв=√(Sв2) 6. Оценка параметров генеральной совокупности по ее выборке (точечная и интервальная). Доверительный интервал и доверительная вероятность. Числовые значения, характеризующие генеральную совокупность, называютсяпараметрами. Статистическое оценивание может выполняться двумя способами: 1)точечная оценка – оценка, которая дается для некоторой определенной точки; 2)интервальная оценка – по данным выборки оценивается интервал, в котором лежит истинное значение с заданной вероятностью. Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности. Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками. Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки. Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя 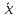 в: в: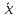 в= в=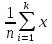 ini, ini,где xi – варианты выборки; ni – частота встречаемости вариант xi; n – объем выборки. Интервальная оценка – это числовой интервал, который определяется двумя числами – границами интервала, содержащий неизвестный параметр генеральной совокупности. Доверительный интервал – это интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности. Доверительная вероятность p – это такая вероятность, что событие вероятности (1-р) можно считать невозможным. α=1-р – это уровень значимости. Обычно в качестве доверительных вероятностей используют вероятности, близкие к 1. Тогда событие, что интервал накроет характеристику, будет практически достоверным. Это р≥0,95, р≥0,99, р≥0,999. Для выборки малого объема (n<30) нормально распределенного количественного признака х доверительный интервал может иметь вид: 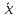 в-m в-m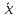 t≤ t≤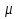 ≤ ≤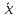 в+m в+m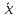 t (р≥0,95), t (р≥0,95), где 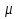 – генеральное среднее; – генеральное среднее; 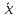 в – выборочное среднее; t – нормированный показатель распределения Стьюдента с(n-1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал; m в – выборочное среднее; t – нормированный показатель распределения Стьюдента с(n-1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал; m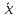 – ошибка выборочной средней. – ошибка выборочной средней.7. Общая постановка задачи проверки гипотез. Параметрические и непараметрические статистические критерии. Общая постановка задачи проверки гипотез: 1. Формулируют (выдвигают) нулевую гипотезу H0 об отсутствии различий между группами, об отсутствии существенного отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др. Сущность нулевой гипотезы H0: разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, то есть эти выборки принадлежат одной генеральной совокупности. 2. Формулируют противоположную нулевой, альтернативную гипотезу H1. 3. Задают уровень значимости α. Уровень значимости α – это вероятность ошибки отвергнуть нулевую гипотезу H0, если на самом деле эта гипотеза верна. При α≤0,05 ошибка возможна в 5% случаев. 4. Для проверки выдвинутой гипотезы используют критерии. Критерий – это случайная величина К. которая служит для проверки H0. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости α. Фактическую величину критерия получают по данным наблюдения Кнабл. 5. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно Ккрит(α,f). 6. Сравнивают Кнабл и Ккрит(α,f). Если Кнабл> Ккрит(α,f), то отвергают H0 и принимают H1. Если Кнабл<Ккрит(α,f), то принимают H0. Это для параметрических критериев. Если использованы непараметрические критерии, то наоборот: если Кнабл> Ккрит(α,f), то принимают H0. 7. Вывод: различие статистически значимо (α≤0,05) или незначимо. Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности. Из которых взяты выборки, подчиняются нормальному закону распределения. Непараметрические критерии применяются, если нет подчинения распределения нормальному закону. Эти критерии обычно заменяют данные выборки знаками (+ или -), рангами (т.е. числами 1; 2; 3;…, описывающими их положение в упорядоченном наборе данных), категориями и т.п. Непараметрический критерий можно использовать, если объем выборки небольшой настолько, что невозможно оценить закон распределения данных. 8. Проверка гипотез относительно генеральных средних и относительно генеральных дисперсий. ОТНОСИТЕЛЬНО СРЕДНИХ: Предположим, что надо сравнить состояние больных до и после лечения. Для этого сравнивают друг с другом две независимые выборки объемом n1 и n2, взятые из нормально распределенных совокупностей с параметрами M(X1) и M(X2). Дополнительно предполагаем, что независимые генеральные дисперсии равны между собой. По этим выборкам найдены соответствующие выборочные средние 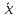 1 и 1 и 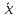 2 и исправленные дисперсии S12 и S22. Уровень значимости задан. 2 и исправленные дисперсии S12 и S22. Уровень значимости задан.
Величину критерия находим по формуле: 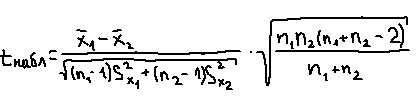 Обычно расчет ведется на ЭВМ. Доказано, что величина tнабл при справедливости нулевой гипотезы имеет t-распределение Стьюдента с f=n1+n2-2 степенями свободы
Если |tнабл| Если наоборот, то отвергается Н0 и принимается H1, различие достоверно. ОТНОСИТЕЛЬНО ДИСПЕРСИЙ: Пусть генеральная совокупность Х1 и Х2 распределены нормально. По независимым выборкам объемом n1 и n1, извлеченных из этих совокупностей, найдены исправленные выборочные дисперсии Sx12 и Sx22. Требуется сравнить эти дисперсии. При заданном уровне значимости α, надо проверить нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.
Из таблицы находим Fкрит(α, f1, f2).
9. Закон распределения случайной величины. Проверка гипотез о законах распределения случайных величин. Выдвигают нулевую гипотезу Н0: неизвестная функция распределения F(x) исследуемой случайной величины X распределена по некоторому теоретическому закону, например, по нормальному закону: H0: F(x)=Fтеор(х). В качестве этой теоретической модели Fтеор(х) может быть рассмотрен любой закон, например, экспоненциальный или биномиальное распределение. Это определяется сущностью изучаемого явления, а также результатами предварительной обработки наблюдений: формой графика распределения, соотношения между выборочными данными. Выдвигается альтернативная гипотеза, что данная генеральная совокупность не распределена по закону Fтеор(х): |

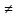 M(X2).
M(X2). σх22.
σх22.