явления перноса в твердых телах. курсовая 1. Закон теплопроводности Физический смысл коэффициента теплопроводности

• Название: Закон теплопроводности Физический смысл коэффициента теплопроводности
• Анкор: явления перноса в твердых телах
• Дата: 07.04.2023
• Размер: 47.5 Kb.
• Имя файла: курсовая 1.docx
• Тип: Закон; #1043744

Содержание

Введение

Явления переноса

Основной закон теплопроводности

Физический смысл коэффициента теплопроводности

Теплопроводность в газах.

Диффузия. Вязкость.

Заключение

Литература

Введение

Беспорядок теплового движения молекул газа, постоянные столкновения между ними приводят к постоянному перемешиванию частиц и изменению их скоростей и энергий. Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения отдельных слоев газа, то движение молекул выравнивает эти неоднородности. В этом случае в газе возникают явления; диффузия, вязкость и теплопроводность.

Целью данной курсовой работы является изучение явления переноса в газах.

В моей курсовой работе анализируются основные особенности процессов переноса в газах, что такое вязкость, диффузия и теплопроводность. Актуальность моей работы состоит в том, что эти явления широко применяется во многих отраслях промышленности. Например, вакуумная техника имеет огромное значение для производства электровакуумных приборов – радиоламп, фотоэлементов и др.

Новизной является то, что я собрал и проанализировал найденный мною материал в одну работу, а также привела к теоретической части несколько примеров и задач на заданную тему.

Под полезностью подразумевается анализ формул и соотношений, формулировка и иллюстрация основных понятий и законов.

1. Явления переноса

В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса. В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движения (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным. В противном случае - это нестационарный процесс. Стационарные процессы возможны только в стационарных внешних условиях. В термодинамически изолированной системе могут возникать только нестационарные явления переноса, направленные на установление равновесного состояния.

Статистическая физика имеет дело с равновесными состояниями и обратимыми процессами (т.е. процессами, при которых система проходит через последовательность равновесных состояний). Наука, изучающая эти процессы, возникающие при нарушениях равновесия, носит название физической кинетики.

При нарушении равновесия система стремится вернуться в равновесное состояние. Этот процесс сопровождается возрастанием энтропии и, следовательно, необратим. Таким образом, процессы, изучаемые физической кинетикой, являются необратимыми.

Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо электрического заряда и т.п. В связи с этим соответствующие процессы носят название явлений переноса. Из сказанного выше вытекает, что явления переноса представляют собой необратимые процессы.

Мы рассмотрим три явления переноса: диффузию, теплопроводность и внутреннее трение, или вязкость, причем ограничимся случаем, когда отклонения от равновесия невелики.

2. Основной закон теплопроводности

Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.

Связь между количеством теплоты Q проходящим за промежуток dt через элементарную площадку dS, расположенную на изотермической поверхности, и градиентом температуры устанавливается гипотезой Фурье, согласно которой

 Q  dSgradTdtTdSdtn/ .(2.1)

Минус в правой части показывает, что в направлении теплового потока температура убывает и grad T является величиной отрицательной. Коэффициент пропорциональности  теплопроводности или более кратко теплопроводностью. Справедливость гипотезы Фурье подтверждено многочисленными опытными данными, поэтому эта гипотеза в настоящее время носит название основного уравнения теплопроводности или закона Фурье.

Отношение количества теплоты, проходящего через заданную поверхность, ко времени называют тепловым потоком. Тепловой поток обозначают q и выражают в ваттах (Вт):

q-T  S (2.2)

n

Если относительное изменение температуры Т на расстоянии средней длины свободного пробега частиц l мало, то выполняется основной закон теплопроводности (закон Фурье): плотность теплового потока q пропорциональна градиенту температуры grad T, то есть

(2.3)

(где  — коэффициент теплопроводности или просто теплопроводности) Отношение теплового потока dq через малый элемент поверхности к площади dS этой поверхности называют поверхностной плотностью теплового потока (или вектором плотности теплового потока), обозначают j и выражают в ваттах на квадратный метр (Вт/м2):

.(2.4)

Вектор плотности теплового потока направлен по нормали к поверхности в сторону убывания температуры. Векторы j и grad T лежат на одной прямой, но направлены в противоположные стороны.

Тепловой поток q, прошедший сквозь произвольную поверхность S, находят из выражения

.(2.5)

Количество теплоты, прошедшее через эту поверхность в течение времени t, определяется интегралом

.(2.6)

Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.

3. Физический смысл коэффициента теплопроводности

Вспомним ещё раз, что основным законом передачи тепла теплопроводностью является закон Фурье. Согласно этому закону количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный тепловому потоку, за время d прямопропорционально температурному градиенту t/n, поверхности dF и времени d:

(3.1)

Коэффициент пропорциональности  называется коэффициентом теплопроводности, при выражении Q в ккал/ч:




Таким образом, коэффициент теплопроводности  показывает, какое количество тепла проходит вследствие теплопроводности в единицу времени


через единицу поверхности теплообмена при падении температуры на 1 град на единицу длины нормали к изотермической поверхности.

Коэффициенты теплопроводности  сплошных однородных сред зависят от физико-химических свойств вещества (структура вещества, его природа). Значения теплопроводности для многих веществ табулированы и могут быть легко найдены в справочной литературе.

Значения коэффициента теплопроводности для некоторых газов, жидкостей и твёрдых тел при атмосферном давлении, зависит от агрегатного состояния вещества (см. табл.), его атомно-молекулярного строения, температуры и давления, состава (в случае смеси или раствора) и т. д.].

Вещество	t,	, вт/(мК)
Газы Водород Гелий Кислород Азот Металлы Серебро Медь Железо Олово Жидкости Ртуть Вода Ацетон Бензол	0 0 0 -3 0 0 0 0   0 20 16  22,5	0,1765 0,1411 0,0237 0,0226   403 86,5 68,2 35,6   0,190 0,167 0,158 6,9

4. Теплопроводность газов

Для идеального газа, состоящего из твёрдых сферических молекул диаметром d, согласно кинетической теории газов, справедливо следующее выражение

(3.4)

где — плотность газа, c_v — теплоёмкость единицы массы газа при постоянном объёме, V — средняя скорость движения молекул. Поскольку J пропорциональна 1/р, а р (р — давление газа), то Т. такого газа не зависит от давления. Кроме того, коэффициент теплопроводности и вязкости связаны соотношением: . В случае газа, состоящего из многоатомных молекул, существенный вклад в дают внутренние степени свободы молекул, что учитывает соотношение:

,

где = ср/c_v, ср — теплоёмкость при постоянном давлении. В реальных газах коэффициент теплопроводности — довольно сложная функция температуры и давления, причём с ростом Т и р значение возрастает. Для газовых смесей может быть как больше, так и меньше коэффициента теплопроводности компонентов смеси, то есть теплопроводности - нелинейная функция состава.

Если газ неравномерно нагрет, т. е. температура в одной его части выше или ниже, чем в другой, то наблюдается выравнивание температуры: более нагретая часть охлаждается, тогда, как более холодная нагревается.

Очевидно, что это связано с потоком тепла от более нагретой части газа к более холодной. Это явление возникновения потока тепла в газеназывается теплопроводностью, В любом теле, в частности в газе, предоставленном самому себе, теплопроводность приводит к выравниванию температур, и этот процесс, конечно, нестационарный. Но часто встречаются и случаи, когда разность температур искусственно поддерживается постоянной.

Например, в электрической лампе накаливания газ, находящийся непосредственно около накаленной нити, имеет высокую температуру (равную температуре самой нити), тогда как газ, прилегающий к стенкам стеклянного баллона лампы, обладает значительно более низкой температурой. Через некоторое время после включения лампы устанавливается постоянная разность температур между нитью и стенками. Это постоянство обеспечивается, с одной стороны, электрической энергией, подводимой к нити из электрической сети, с другой стороны — отдачей тепла от стенок лампы к окружающему ее воздуху. При этих условиях в газе, находящемся в лампе, устанавливается стационарный, т. е. не изменяющийся со временем, поток тепла. Установившаяся стационарная разность температур зависит от теплопроводности газа (для лампы накаливания надо иметь в виду, что кроме отвода тепла через газ в данном частном случае отвод тепла происходит главным образом в результате излучения).

В приведенном примере лампы расчет потока тепла представляет большие трудности, связанные со сложной формой нити и сосуда, вследствие чего распределение температуры в газе тоже оказывается весьма сложным.

Чтобы найти количественные закономерности, характеризующие процесс теплопроводности, мы рассмотрим более простую задачу

Пусть вдоль какого-нибудь направления в газе, например, вдоль осиX,температура меняется отточки к точке,т. е. является функцией v. в то время как в плоскости, перпендикулярной к этой оси, температура всюду одинакова



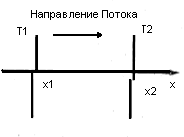
Изменение температуры вдоль оси X характеризуется градиентом температуры .

Смысл градиента температуры заключается в том, что он равен изменению температуры от одной точки к другой, отнесенному к единице расстояния между ними. Существование градиента температуры и является необходимым условием для возникновения теплопроводности. Направление потока тепла совпадает с направлением падения температуры. Если возрастанию х (т. е. dx> 0) соответствует падение температуры (dТ<0), то тепло течет в направлении возрастающего х: поток тепла направлен так, чтобы уменьшить существующий градиент температуры, который его вызвал. Опыт показывает, что поток тепла Qпропорционален градиенту температуры (закон Фурье): (3.5)

При стационарных условиях количество тепла Q, протекающего в единицу времени через газ, равно мощности источника энергии, за счет которого поддерживается заданный градиент температуры. Эта мощность (обычно электрическая) и подлежит измерению при экспериментальном определении коэффициента теплопроводности. В тех случаях, когда газ, в котором существует градиент температуры, предоставлен самому себе, т. е. к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Сначала мы и рассмотрим такую нестационарную теплопроводность. Как мы увидим, закон выравнивания температуры весьма напоминает процесс выравнивания концентрации посредством диффузии.

Диффузия

Диффузия (от лат. diffusio — распространение, растекание), взаимное проникновение соприкасающихся веществ друг в друга вследствие теплового движения частиц вещества. Диффузия происходит в направлении падения концентрации вещества и ведёт к равномерному распределению вещества по всему занимаемому им объёму (к выравниванию химического потенциала вещества).
Самым известным примером диффузии является перемешивание газов или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Диффузия крупных частиц, взвешенных в газе или жидкости (например, частиц дыма или суспензии), осуществляется благодаря их броуновскому движению. В дальнейшем, если специально не оговорено, имеется в виду молекулярная диффузия. Наиболее быстро она происходит в газах, медленнее в жидкостях, ещё медленнее в твёрдых телах, что обусловлено характером теплового движения частиц в этих средах. Траектория движения каждой частицы газа представляет собой ломаную линию, т.к. при столкновениях частицы меняют направление и скорость своего движения. Неупорядоченность движения приводит к тому, что каждая частица постепенно удаляется от места, где она находилась, причём её смещение по прямой гораздо меньше пути, пройденного по ломаной линии. Поэтому диффузионное проникновение значительно медленнее свободного движения (скорость диффузионного распространения запахов, например, много меньше скорости молекул).

Феномен переноса - диффузии - состоит в самопроизвольном взаимном проникновении и смешивании частиц двух контактирующих газов, жидкостей и даже твердых тел. В то же время различается самодиффузия - проникновение атомов и молекул одного и того же вида между молекулами одного типа и гетеродиффузия - проникновение молекул или атомов одного вида между атомами или молекулами другого рода. В химически чистых газах диффузия происходит из-за неодинаковой плотности в разных частях объема газа. В случае газовой смеси причиной диффузии является разница в концентрации отдельных газов в разных частях объема смеси. Если это явление не осложняется изменением температуры по объему газа, то оно заключается в переносе массы газа из мест с более высокой концентрацией данного газа в места с более низкой концентрацией.

Экспериментально установлено, что перенос массы вещества при явлении диффузии подчиняется закону А. Фика.

Масса газа, которая передается в единицу времени через элемент поверхности, взятый внутри газа, площадь которого равна единице, прямо пропорциональна скорости изменения плотности газа r на единицу длины x в направлении нормаль к рассматриваемой области.

Если элемент поверхности выбран так, что нормаль совпадает с направлением самого быстрого уменьшения плотности r, то он численно равен градиенту плотности. Значение D называется коэффициентом диффузии. Коэффициент диффузии - это физическая величина, численно равная массе вещества, переносимого через единицу поверхности за единицу времени с градиентом плотности, равным единице. В системе единиц СИ коэффициент диффузии измеряется в м2 / с, в системе CGS - в см2 / с. Знак минус в формуле (10.5) указывает на то, что массообмен происходит в направлении уменьшения плотности.

Феномен внутреннего трения (вязкости) связан с возникновением сил трения между слоями газа или жидкости, движущимися параллельно друг другу с разными скоростями. Со стороны слоя, движущегося быстрее, на медленный движущийся слой действует ускоряющая сила. И наоборот, медленно движущийся слой замедляет более быстро движущиеся слои газа. Силы трения, возникающие в этом случае, направлены тангенциально к поверхности контакта слоев.

С точки зрения кинетической теории газов причиной внутреннего трения является суперпозиция упорядоченного движения слоев газа с разными скоростями V1 и V2 и хаотического теплового движения молекул, интенсивность которого зависит от температуры. Из-за теплового движения молекулы движутся от слоя B, движущегося со скоростью V2, к слою A, движущемуся со скоростью V1.

В этом случае молекулы из слоя B «переносят» на слой A импульсы mV2 своего упорядоченного движения. Если V1> V2, то такие молекулы при столкновениях с частицами слоя А ускоряют свое упорядоченное движение, а молекулы слоя А замедляются. Напротив, когда молекулы переходят из быстро движущегося слоя A в слой B, они передают большие импульсы mV1, и столкновения между молекулами приводят к ускорению упорядоченного движения молекул слоя B.

Заключение

В своей работе я рассматривал явления переноса в газах. В общем случае я выяснил, что коэффициент теплопроводности для некоторых газов, жидкостей и твёрдых тел при атмосферном давлении, зависит от агрегатного состояния вещества (что видно, если посмотреть таблицу в моей курсовой работе, а лучше, к примеру, книгу о теплопроводности жидкостей и газов где приведены все газы и жидкости и подсчитан для некоторой температуры), его атомно-молекулярного строения, температуры и давления, состава (в случае смеси или раствора).

Если подробно рассматривать газа и жидкости , то как и для газа так и для жидкостей было сделано много различных опытов, впоследствии которых были получены формулы для определения .

Для различных газов, будь он, идеальный газ или реальный газ или ещё какой-то в конечном итоге видно что если к примеру взять газ идеальный, состоящий из твёрдых сферических молекул диаметром d, согласно кинетической теории газов, была получена конкретная формула для определения , если взять реальный газ, то довольно сложная функция температуры и давления, причём с ростом Т и р значение возрастает, это я рассмотрел как пример для идеального и реального газа, (существуют газовые смеси, газ, состоящий из многоатомных молекул, для определения надо воспользоваться внутренними степенями свободы молекул, и другие примеры газов)

Все рассмотренные примеры характеризуются общим свойством — переносом некоторого признака из одних областей системы в другие. Неслучайно поэтому, что явления такого рода называются явлениями переноса. Каждое из них характеризуется своим коэффициентом переноса, и задача теории — уметь их вычислять. В общем случае это очень трудная задача, до сих пор полностью не решенная.

Оказывается, все три коэффициента (теплопроводности, диффузии и вязкости) пропорциональны длине свободного пробега молекул (l ) и средней скорости их теплового движения (υ ): . Такая зависимость коэффициентов переноса от характеристик молекулярного движения очень естественна. Ведь средняя скорость молекул υ определяет скорость переноса того или иного признака в процессе установления равновесия. Длина же свободного пробега l появляется в формуле потому, что после каждого столкновения параметры движения молекулы определяются параметрами системы в тех местах, где эти столкновения происходят, то есть в точках, отстоящих друг от друга на расстояние l. Так, в нашем примере с теплопроводностью величина энергии, передаваемой молекулой при очередном столкновении, определяется разностью температур в тех точках среды, где произошло это и предыдущее столкновение.

В данной курсовой работе были рассмотрены явления переноса в твердых телах. Явления переноса объединяют группу процессов, связанных с выравниванием неоднородностей плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества.

Список используемых источников

1. Нащокин В.В.Техническая термодинамика и теплопередача

2. А.К. Кикоин, И.К. КикоинОбщий Курс Физики – Молекулярная Физика

3. Миснар А. Теплопроводность твердых тел, жидкостей, газов и ихкомпозиций.

4. Интернет - wikipendia.ru (интернет энциклопедия)

1. Ашкрофт Н., Мермин Н. Физика твердого тела: Пер. с англ. В 2-х т. М.: Мир, 1979. Т. 1, Т. 2

2. Городецкий Е.Е. О явлениях переноса //Квант. — 1986. — № 9. — С. 27-29.

3. Епифанов. Г. И. Физика твердого тела. М.: Высшая школа,1977.

4. Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.

5. Шьюмон П., Диффузия в твердых телах, пер. с англ., М., 1966