Лекция 4. Закон термодинамики
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ Первый закон термодинамики устанавливает эквивалентность теплоты и работы при их взаимном превращении, но не указывает направления преобразования энергии и не устанавливает условий и границ их взамопревращений. Если механическую энергию можно полностью преобразовать в тепловую (например, путем трения), то обратное преобразование тепловой энергии в механическую можно осуществить только при соблюдении определенных условий, при этом не вся тепловая энергия превратится в работу. Второй закон термодинамики устанавливает условия преобразования тепловой энергии в механическую и показывает, какую часть теплоты можно превратить в работу. Рассмотрим простейшую схему паросиловой установки, в которой теплота превращается в работу (рис. 3.1).   Рис. 3.1. Схема паросиловой установки В котле 1 за счет теплоты q1, выделившейся при горении топлива, вода превращается в пар. Пар по трубопроводу поступает в пароперегреватель 2, в котором сушится, перегревается и посредством соплового аппарата, где существенно увеличивается его скорость, подается в турбину 3 паровой машины, которая вращает вал электрического генератора 4 – потребителя вырабатываемой механической энергии. В турбине пар, расширяясь, совершает работу. После расширения отработавший пар поступает в конденсатор 5, где конденсируется за счет охлаждающей воды, отдавая последней теплоту конденсации q2. Образовавшийся конденсат насосом 6 перекачивается в сборник конденсата 7, затем насосом 8 через подогреватель конденсата 9 подается в котел 1. Из приведенного примера видно: 1) не вся теплота превратилась в работу:  ; ;отнятая от рабочего тела в конденсаторе теплота не может быть использована для дальнейшего преобразования в механическую энергию; 2) превращение теплоты в работу возможно только при наличии не менее двух источников теплоты: верхнего – топка котла (горячий источник) и нижнего – конденсатора (холодный источник). Полученные выводы были положены в основу второго закона термодинамики, имеющего несколько формулировок: 1. Планк сформулировал его следующим образом: «Невозможно построить периодически действующий двигатель, который производил бы только поднятие груза и охлаждение источника теплоты». 2. Оствальд: «Невозможно построить вечный двигатель второго рода» (двигатель, работающий при наличии только одного источника теплоты). 3. Клаузиус: «Теплота не может переходить от менее нагретого тела к более нагретому телу без компенсации». Второй закон термодинамики первым обосновал Карно. При исследовании принципа работы периодически действующей тепловой машины он установил 3 постулата: Для превращения теплоты q в работу l необходимо иметь не менее двух источников теплоты (холодный и горячий); Не вся подведенная теплота превращается в работу; Чем выше температура горячего источника T1 и чем ниже температура холодного источника T2, тем большая часть подведенной теплоты q будет превращена в работу. 3.1. Круговые процессы или циклы Из изложенного в предыдущем разделе следует, что, имея рабочее тело и источники теплоты, рабочее тело при расширении может преобразовать тепловую энергию в механическую (например, в цилиндре с поршнем). Это преобразование возможно до тех пор, пока давление рабочего тела pраб.т не станет равным давлению окружающей среды pсреды. Когда эти давления становятся равными (pраб. т.= pсреды), дальнейшее преобразование теплоты в работу невозможно. Чтобы такое преобразование было непрерывным, нужно рабочее тело в цилиндре вернуть в исходное состояние, то есть необходимо осуществить круговой процесс, который называется циклом. Рассмотрим этот процесс в pυ-диаграмме. 1 кг газа, расширяясь, из состояния 1 переходит в состояние 2 (процесс 1а2, рис. 3.2). Работа расширения lрасш. = пл.1а2341. Путем сжатия рабочее тело возвращается в исходное состояние 1 по тому же процессу 2а1. При сжатии затрачивается работаlсж= пл.1а2341. Результирующая работа lрез.= lрасш. lсж= 0. Полезная работа не совершается, такой цикл не имеет смысла.   Рис. 3.2. Цикл, при ко- тором полезная работа не совершается Допустим, расширение 1 кг рабочего тела происходит в процессе 1а2 (рис. 3.3а). При этом к телу подводится теплота q1. Сжатие происходит в процессе 2в1, и от рабочего тела отводится теплота q2. Работа расширения lрасш.определяется площадью 1а2341, работа сжатия lсж площадью 1в2341. Результирующая работа lрез= lрасш lсж> 0 определяется площадью цикла 1а2в1. В нашем случае результирующая работа lрезпредставляет собой работу цикла lц. Цикл, в результате которого совершается положительная работа, называется прямым циклом (циклы тепловых двигателей). Степень совершенства прямых циклов характеризуется термическим коэффициентом полезного действия (термический КПД), под которым понимается доля подведенной теплоты, превращенная в работу: 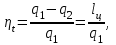 (3.1) (3.1)
где lц = q1 – q2. Термический КПД всегда меньше единицы, и только при q2=0 t=1, чего практически осуществить невозможно. Если в цикле 1в2а1 (рис. 3.3б) расширение происходит в процессе 1а2 с подводом теплоты q2, а сжатие в процессе 2в1 с отводом теплоты q1, lрасш< lсж. Тогда результирующая работаlрез.= lрасш. lсж< 0, то есть на осуществление цикла затрачивается работа. Такие циклы называются обратными (циклы холодильных установок). Степень совершенства обратных циклов характеризуется холодильным коэффициентом 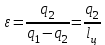 . .Циклы бывают обратимыми и необратимыми. Обратимые циклы состоят только из обратимых процессов. Если хоть один процесс в цикле необратимый, то и цикл будет необратимым. Задачу о том, в каком случае подведенная теплота максимально будет превращаться в работу, впервые решил французский инженер и ученый Сади Карно. Он предложил цикл, который состоит из двух изотерм и двух адиабат (рис. 3.4). Термический КПД цикла Карно имеет наибольшее значение по сравнению с КПД любого цикла, осуществляемого при тех же температурах, и является эталоном при оценке степени совершенства циклов реальных двигателей.  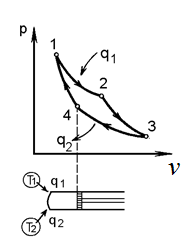 Рис. 3.4. Прямой цикл Карно в координатах рv Для осуществления этого цикла нужно иметь горячий источник теплоты с температурой Т1, холодный источник с температурой Т2, 1 кг идеального газа (рабочего тела), поршень и цилиндр с абсолютно нетеплопроводными стенками. Процессы подвода и отвода теплоты не должны влиять на состояние источников, то есть температуры их должны оставаться постоянными. Рабочее тело с параметрамиp1,v1 (точки 1 в pv-диаграмме), соприкасаясь с горячим источником Т1, получает теплоту q1 и расширяется при Т1=const. Чтобы процесс расширения был обратимым, он должен происходить при отсутствии разности температур между источником и рабочим телом, то есть по изотерме 1–2. В точке 2 горячий источник отключается, и дальнейшее расширение рабочего тела происходит по адиабате 23 за счет внутренней энергии. В результате температура газа понижается до Т2. В точке 3 рабочее тело подключается к холодному источнику с температурой Т2 и сжимается по изотерме 34 при Т2=const, отдавая ему теплоту q2. В точке 4 холодный источник отключается, и дальнейшее сжатие происходит по адиабате 41. Работа, затраченная на сжатие, идет на увеличение внутренней энергии, а это приводит к увеличению температуры до Т1. После этого цикл повторяется.  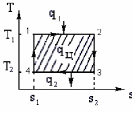 Рис. 3.5. Прямой обратимый цикл Карно в координатах Тs Рис. 3.5. Прямой обратимый цикл Карно в координатах ТsНа тепловой Тs-диаграмме (рис. 3.5) площадь 12s2s11 соответствует количеству подведенной теплоты q1, площадь 43s2s14 – количеству отведенной теплоты q2. Следовательно, q1 = T1(s2 – s1); q2 = T2(s2 – s1). Термический КПД цикла Карно    . (3.2) . (3.2)Формула (3.2) показывает следующее: 1) термический КПД цикла Карно зависит только от температуры горячего и холодного источников теплоты, то есть  ; ;2) при наличии только одного источника теплоту в работу превратить нельзя (Т1=Т2; lц=0, t=0); 3) невозможно превратить всю подведенную теплоту в работу (q1 = lц), то есть термический КПД цикла не может достичь значения, равного единице, так как для этого необходимо, чтобы T1= или Т2=0, что неосуществимо; 4) чем выше температура горячего источника T1и чем ниже температура холодного источника Т2, тем больше КПД и тем большая часть подведенной теплоты превращается в работу; 5) термический КПД цикла Карно не зависит от физических свойств рабочего тела. Последнее положение известно под названием теоремы Карно. Оно следует из того, что формула (3.2) не содержит величин, характеризующих свойства рабочего тела, а использованные для ее вывода выражения q1 и q2 справедливы для любого тела. Обратный цикл Карно, так же, как и прямой, состоит из двух адиабат и двух изотерм, но рабочее тело изменяет свое состояние в направлении против вращения часовой стрелки, в связи с чем изотерма расширения располагается ниже изотермы сжатия (рис. 3.6). Газ с начальным состоянием, определяемым параметрами точки 1, расширяется по адиабате 12 за счет уменьшения внутренней энергии, при этом температура газа понижается от Т1 до Т2. В точке 2 рабочее тело подключается к холодному источнику с температурой Т2 и в изотермическом процессе 23 отбирает теплоту q2 у охлаждаемого нижнего источника тепла. В точке 3 процесс расширения заканчивается и начинается адиабатное сжатие 34, в результате которого температура рабочего тела повышается до температуры горячего источника Т1.  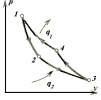 Рис. 3.6. Обратный обратимый цикл Карно в координатах pv В точке 4 рабочее тело подключается к горячему источнику с температурой Т1 и в изотермическом процессе 41 отдает ему теплоту: q1 = q2+lц. Таким образом, в результате затраченной в процессе сжатия 3-4-1 работы lсж произошла передача теплоты от менее нагретого тела к более нагретому. При этом горячему источнику передается не только теплота q2, но и часть превращенной в теплоту работы lц, определяемой площадью цикла 1-2-3-4. Степень совершенства обратного обратимого цикла Карно определяется холодильным коэффициентом 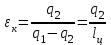 . .Учитывая, что в цикле Карно q1 = T1(s2 – s1), а q2 = T2(s2 – s1), окончательно получим  . (3.3) . (3.3)Чем больше Т2, тем больше . При неизменном значении Т2 цикл экономичнее при более низком значении Т1. 3.2. Общие свойства обратимых и необратимых циклов Термический КПД цикла Карно определяется из выражения (3.1) или (3.2), то есть в цикле Карно 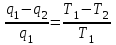 или 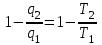 ; ; ; ;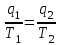 . .В соответствии с принятым правилом знаков величина теплоты q1, подводимой к рабочему телу, считается положительной, а теплоты q2, отводимой от рабочего тела, считается отрицательной. Значит, последнее соотношение можно записать в форме 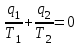 или  (3.4) (3.4)Из выражения (3.4) следует: в обратимом цикле Карно алгебраическая сумма приведенных теплот равна нулю. Рассмотрим произвольный обратимый цикл 1-2-3-4 (рис. 3.7). Разобьем его с помощью адиабат на бесконечное множество элементарных циклов. Каждый из этих циклов образуется двумя адиабатами и двумя элементарными участками основного цикла, которые можно рассматривать как изотермы подвода и отвода теплоты. Таким образом, каждый элементарный цикл является элементарным циклом Карно, для которого в соответствии с выражением (3.4) можно записать:  . .Интегрируя это выражение по верхней ветви подвода теплоты и по нижней ветви отвода теплоты, получим   Рис. 3.7. Произвольный обратимый цикл  или, по аналогии с выражением (3.4) можно записать интегральную сумму и заменить последнее равенство на круговой интеграл:  (3.5) (3.5) В выражениях (3.4) и (3.5) температуры рабочего тела равны температурам источников теплоты, так как мы имеем дело с обратимыми процессами. Количество теплоты, отбираемой от источника, равно количеству теплоты, передаваемой рабочему телу, но знак δqберется относительно рабочего тела, то есть подведенная к рабочему телу теплота положительная, отведенная от рабочего тела – отрицательная. Интеграл (3.5) называется первым интегралом Клаузиуса, и его можно рассматривать как математическое выражение Второго закона термодинамики для обратимых циклов, так как отправным пунктом его доказательства является Второй закон термодинамики. Интеграл (3.5) показывает, что для превращения теплоты в работу нужно иметь горячие (δq>0) и холодные (δq<0) источники теплоты, иначе 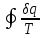 не будет равен нулю. не будет равен нулю.Рассмортим необратимые циклы. Термический КПД обратимого цикла Карно  В этом выражении температура горячего источника Т1 в процессе подвода теплоты равна температуре рабочего тела Т1, температура холодного источника Т2 равна температуре рабочего тела Т2 в процессе отвода теплоты (это условие обратимости процессов). В необратимом цикле Карно Т1 > Т1, а Т2 < Т2. Поэтому процессы подвода и отвода теплоты, а значит, и весь цикл, являются необратимыми. Необратимость вызвана отсутствием температурного равновесия между рабочим телом и источниками теплоты. КПД необратимого цикла Карно 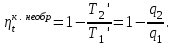 меньше термического КПД обратимого цикла Карно, осуществляемого в том же интервале температур:   . .Учитывая, что q2 теплота отводимая, получим  (3.6) (3.6)где Т1 и Т2 температуры теплоотдатчика и теплоприемника; они не равны температурам рабочего тела при подводе и отводе теплоты. Неравенство (3.6) показывает, что в необратимом цикле Карно алгебраическая сумма приведенных теплот меньше нуля. Как и в предыдущем случае, обобщим полученное неравенство на произвольный необратимый цикл. Для этого необратимый цикл с помощью адиабат разобьем на бесконечное множество элементарных необратимых циклов Карно. Для каждого из этих элементарных циклов можно применить неравенство (3.6) в виде  , ,После интегрирования по участкам подвода и отвода теплоты получим  , ,или 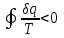 (3.7) (3.7)В этом неравенстве, как и в неравенстве (3.6), температура относится не к рабочему телу, а к теплоотдатчикам и теплоприемникам, и знак qберется относительно рабочего тела. Неравенство (3.7) называется вторым интегралом Клаузиуса, и его можно рассматривать как математическое выражение второго закона термодинамики для необратимых циклов. Объединяя формулы (3.5) и (3.7), получим неравенство  (3.8) (3.8)называемое аналитическим выражением II закона термодинамики. Знак равенства относится к обратимым, а знак неравенства – к необратимым циклам. 3.3. Изменение энтропии в обратимых и необратимых процессах Выражение  , характеризующее обратимые циклы, показывает, что интеграл элементарной приведенной теплоты по замкнутому контуру равен нулю. Следовательно, подынтегральная величина является полным дифференциалом некоторой функции состояния, которая ранее была обозначена символом s и названа энтропией. Её дифференциал для элементарного обратимого процесса записывается в виде , характеризующее обратимые циклы, показывает, что интеграл элементарной приведенной теплоты по замкнутому контуру равен нулю. Следовательно, подынтегральная величина является полным дифференциалом некоторой функции состояния, которая ранее была обозначена символом s и названа энтропией. Её дифференциал для элементарного обратимого процесса записывается в виде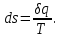 (3.9) (3.9)Проинтегрировав выражение (3.9), можно определить изменение энтропии в обратимом процессе 1 – 2: 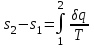 . (3.10) . (3.10)Так как процесс обратимый, температура в формулах (3.9) и (3.10) относится как к источникам теплоты, так и к рабочему телу.   Рис. 3.8. Произвольный Рис. 3.8. Произвольныйнеобратимый цикл Чтобы определить изменение энтропии в необратимых процессах, рассмотрим необратимый цикл (рис. 3.8), который состоит из обратимого процесса (2-4-1) и необратимого (1-3-2), условно изображенного пунктирной линией. Для необратимого цикла согласно неравенству (3.7) 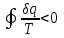 или  (3.11) (3.11)В обратимом процессе 2-4-1  . .Подставив это выражение в неравенство (3.11), получим  . .Отсюда следует, что изменение энтропии в необратимом процессе будет: 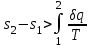 . (3.12) . (3.12)Объединяя выражения (3.10) и (3.12), запишем  . (3.13) . (3.13)Энтропия функция состояния, ее изменение не зависит от характера процесса, а определяется только начальным и конечным состояниями. В рассматриваемом случае начало и конец обратимого и необратимого процессов совпадают, следовательно, изменение энтропии в этих процессах будет одним и тем же. Формулы (3.10) и (3.12) показывают, что в обратимых процессах 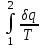 равен изменению энтропии s2s1, а в необратимых равен изменению энтропии s2s1, а в необратимых 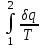 меньше изменения энтропии s2s1. меньше изменения энтропии s2s1.Формулы (3.10) – (3.12), полученные из выражения (3.8), также являются математическим выражением второго закона термодинамики для обратимых и необратимых процессов. Для элементарного необратимого процесса согласно неравенству (3.12)  (3.14) (3.14)Объединяя неравенства (3.9) и (3.14), получим  . (3.15) . (3.15)Знак равенства относится к обратимым, а знак неравенства к необратимым процессам. В неравенстве (3.14) q – элементарное количество теплоты, полученной рабочим телом от источника теплоты; Т – абсолютная температура источника теплоты, при которой она подводится. 3.4. Принцип возрастания энтропии изолированной системы Изолированная система – это система, которая не обменивается теплотой с окружающей средой (q = 0). Если в изолированной системе протекают обратимые процессы, то из уравнения ds = q/T видно, что ds = 0; s = const. Энтропия изолированной системы остается постоянной. Если же в изолированной системе протекают необратимые процессы, то из выражения ds>q/T получим ds>0; то есть происходит увеличение энтропии. Таким образом, энтропия изолированной системы либо остается неизменной (ds = 0, s=const), либо увеличивается (ds>0), но никогда не уменьшается, хотя энтропия отдельных тел, входящих в изолированную систему, может и увеличиваться, и уменьшаться, и оставаться постоянной. Но для всей системы ds 0. Увеличение энтропии изолированной системы при протекании в ней необратимых процессов называется принципом возрастания энтропии. Увеличение энтропии изолированной системы не имело бы особого значения, если бы оно не сопровождалось уменьшением работоспобности системы. Принцип возрастания энтропии является общим выражением второго закона термодинамики, показывающим деградацию (обесценивание) энергии при протекании необратимых процессов. Допустим, изолированная система состоит из двух участков (источников теплоты) с температурами T1 и T2, T1>T2. Необратимым путем, то есть при конечной разности температур, теплота передается от горячего источника к холодному, при этом температура горячего источника понижается, при этом ее способность совершать работу снижается, то есть энергия деградирует, а энтропия системы растет. Через некоторое время температуры выравниваются, система приходит в состояние равновесия, и рост энтропии прекращается, достигнув своего максимального значения. Таким образом, в равновесном состоянии система имеет максимум энтропии и полностью деградированную энергию (не способную совершать работу). Энергия в пределах системы теряет свою работоспособность. Рассмотрим изолированную систему, в которой имеются два источника теплоты Т1 и Т2 и 1 кг рабочего тела (рис. 3.9).    Рис. 3.9. Изолированная система, в которой теплота преобразуется в работу в обратимом и необратимом процессах А Б Подключая рабочее тело к источникам попеременно, превратим теплоту в работу. Для этого в первом случае (А) от источника с температурой Т1 в обратимом процессе отводим теплоту q1 к рабочему телу и посредством цикла Карно преобразуем её в работу l, при этом источнику Т2 отводится теплота q2. Во втором случае (Б) используем промежуточный источник с температурой Т1 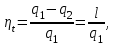 получим l = q1t. В первом случае (А) 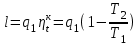 . .Во втором случае (Б)  . .Потеря работы в результате такого необратимого процесса передачи теплоты от источника T1 источнику Т1 составит 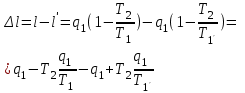 или 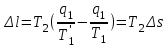 (3.16) (3.16)Это уравнение называется уравнением ГюиСтодолы. Оно устанавливает, что уменьшение работоспособности изолированной системы, в которой протекают необратимые процессы, равно произведению температуры нижнего источника на изменение энтропии этой системы. Чем больше необратимость процессов, тем больше увеличение энтропии, то есть рост энтропии является мерой необратимости процесса, мерой потери работоспособности, мерой деградации энергии. Эксергия. Различные виды энергии имеют неодинаковую практическую пригодность, а также неодинаковую техническую ценность, отнесенную к единице энергии. В качестве всеобщего показателя практической энергетической пригодности (качества) различных форм переноса энергии принята их способность к совершению работы. Второй закон термодинамики утверждает, что, для того чтобы превратить теплоту в работу, нужно иметь не менее двух источников теплоты верхний (горячий) и нижний (холодный), и что не вся теплота может быть превращена в работу. В реальных условиях в качестве нижнего источника теплоты, как правило, используется окружающая среда. Поэтому температура окружающей среды является важным параметром при техническом осуществлении тепловых циклов и оценке практической пригодности энергии. Практическая энергетическая пригодность источника теплоты или рабочего тела равна нулю, если параметры их состояния соответствуют параметрам окружающей среды. Поэтому состояние термодинамического равновесия источника теплоты или рабочего тела с окружающей средой принимается за начало отсчета (нулевой уровень) при рассмотрении их практической энергетической пригодности. Например, окружающая среда располагает неограниченным количеством тепловой энергии, но практическая пригодность этой теплоты равна нулю. Чем ближе параметры источника теплоты к параметрам окружающей среды, тем меньше его практическая пригодность. Различные виды энергии и теплота способны максимально превращаться в работу при выполнении следующих условий: процессы, связанные с превращением энергии, во-первых, должны быть обратимыми, во вторых, должны протекать до состояния равновесия с окружающей средой. Полученная при этих условиях максимальная работа и есть эксергия. Эксергия обозначается как Eх, измеряется в джоулях (Дж). Удельная эксергия  Дж/кг. Дж/кг.Различают эксергию рабочего тела в потоке, эксергию неподвижного рабочего тела и эксергию теплоты. Энергией рабочего тела, способной превращаться в работу, является: в потоке – энтальпия, в неподвижном теле – внутренняя энергия. Энтальпия и внутренняя энергия, как и теплота, не способны полностью превращаться в работу в круговом процессе. Поэтому и возникло понятие эксергии. Эксергия это превратимая часть энергии, то есть та часть энергии, которая может превращаться в работу при сформулированных выше условиях. Непревратимая часть энергии называется анергией. Эксергия теплоты. Рассмотрим систему, которая состоит из теплоотдатчика с температурой Т, теплоприемника (окружающая среда с температурой То) и рабочего тела массой 1 кг. Располагаемое количество теплоты q. Эксергия теплоты это максимальная работа, которую можно получить из этой теплоты. Она равна работе обратимого цикла Карно: 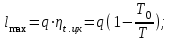 то есть эксергия теплоты определяется из выражения  (3.22) (3.22)Эксергия рабочего тела в потоке. Определить эксергию рабочего тела в потоке значит определить максимальную работу, которую может совершать рабочее тело в потоке при обратимом переходе из состояния с параметрами р и Т в состояние равновесия с окружающей средой с параметрами ро, То. Чтобы процесс был обратимым, он должен протекать по изотерме при температуре окружающей среды. Но для этого надо температуру рабочего тела предварительно понизить до температуры окружающей среды, не допуская необратимости. Это можно сделать, исключив теплообмен. Поэтому сначала путем адиабатного расширения (рис. 3.11, 3.12, процесс 1-а) охлаждаем рабочее тело до температуры окружающей среды То, затем по изотерме а0 понижаем давление до давления ро. Максимальная работа lmax = lад.+lТ. Работу потока в адиабатном процессе lад., которая в pv-диаграмме характеризуется площадью аbf1а, определяем из уравнения 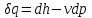 . (3.23) . (3.23)Для этого интегрируем выражение (3.23) по адиабате 1а:  , ,где  – элементарная работа потока. В адиабатном процессе  , ,следовательно, 
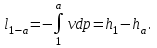 (3.24) (3.24)Превращенная в работу энтальпия h1-ha в Тs-диаграмме изображается заштрихованной площадью 1sasbb1. Работа в изотермическом процессе определяется также из выражения (3.23) путем интегрирования его по изотермическому процессу а-0:  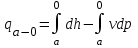 или 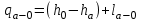 (3.25) (3.25)В изотермическом процессе а-0  . .Подставим это выражение в формулу (3.25) и получим 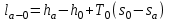 (3.26) (3.26)Работа в изотермическом процессе lа-0 в pv-диаграмме изображается площадью 0аbс0, теплота и энтальпия, превращенные в эту работу, – площадью 0аsas00 в Ts-диаграмме. Просуммировав уравнения (3.24) и (3.26), получим максимальную работу, или эксергию рабочего тела в потоке:  или  , (3.27) , (3.27)так как sa = s1. Эксергия неподвижного рабочего тела. Допустим, рабочее тело находится в цилиндре с подвижным поршнем. Параметры рабочего тела u, s, v, T, p. Параметры окружающей среды u0, s0, v0, T0, p0. Задача определения эксергии неподвижного рабочего тела, как и для потока, сводится к определению максимальной работы, которую может произвести система при обратимом переходе всех ее параметров в состояние равновесия с окружающей средой. В данном случае мы рассматриваем закрытую систему, то есть обмен веществом через границы системы исключен. Среда и система взаимодействуют только в форме теплоты (термическое взаимодействие) и в форме работы (деформационное взаимодействие). Максимальная работа, совершаемая на элементарном участке процесса при термическом взаимодействии:  при деформационном взаимодействии l. Часть деформационной работы l= podv затрачивается на преодоление давления окружающей среды. Поэтому с пользой может быть использована только часть деформационной работы: 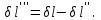 Таким образом, эксергия, или максимальная полезная работа системы на элементарном участке процесса  Из первого закона термодинамики: 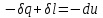 , ,а из второго закона термодинамики:  . .Следовательно, 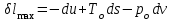 . .После интегрирования по процессу получим 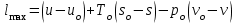 или  . (3.28) . (3.28)Если все процессы, связанные с преобразованием энергии, протекают обратимо, то эксергия системы остается неизменной. Эксергия в начале процесса равна эксергии в конце процесса:  . .Если при этом часть энергии преобразуется в работу, работа lmax будет максимальной: 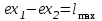 Если же в системе протекают необратимые процессы, то происходит потеря эксергии: 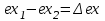 , ,где  – потеря удельной эксергии из-за необратимости процесса. Если при этом часть энергии превращается в работу, работа l не будет максимальной: – потеря удельной эксергии из-за необратимости процесса. Если при этом часть энергии превращается в работу, работа l не будет максимальной: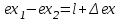 Потеря эксергии теплоты  ; ;где  – удельная работа, совершающаяся в цикле Карно, а – удельная работа, совершающаяся в цикле Карно, а потеря удельной эксергии теплоты. потеря удельной эксергии теплоты.Если цикл полностью обратимый,  , ,то есть  и ex = 0. и ex = 0.  Рис. 3.13. Диаграмма потери энергии в результате необратимого теплообмена Следовательно, с помощью обратимого цикла Карно можно превращать теплоту или часть её в работу без потерь, то есть без обесценивания энергии. Рассмотрим необратимый процесс теплообмена между двумя источниками теплоты, при этом принимаем l=0, аq1=q2=q(рис. 3.13):  . (3.29) . (3.29)Источник теплоты с температурой Т1 отдает теплоту q, при этом его энтропия уменьшается на  . .Источник с температурой Т2 воспринимает то же количество теплоты q, и его энтропия увеличивается на  . .Удельная энтропия системы изменится на 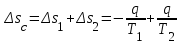 . .Подставив это выражение в формулу (3.29), получим 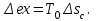 (3.30) (3.30)Потеря удельной эксергии теплоты определяется произведением абсолютной температуры окружающей среды на приращение энтропии системы от необратимости процесса. В диаграмме Tsпотеря эксергии изображается заштрихованной площадью прямоугольника. Потеря эксергии тем больше, чем больше приращение энтропии, вызванное необратимостью процесса. Потеря эксергии рабочего тела в потоке: 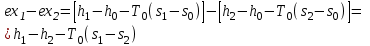 , , где 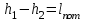 – удельная полезная работа в адиабатном потоке; – удельная полезная работа в адиабатном потоке;− 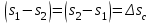 – приращение удельной энтропии системы. Тогда – приращение удельной энтропии системы. Тогда или  , , . (3.31) . (3.31)Таким образом, потеря эксергии потока и потеря эксергии теплоты описываются одинаковыми уравнениями (3.31) и (3.30). 3.7.Эксергетический баланс и эксергетический КПД При исследовании совершенства тепловых процессов путем составления энергетического (теплового) баланса не учитывается качество различных видов энергии. Поэтому энергетический баланс не дает возможности установить процессы, снижающие степень совершенства тепловой установки, и не позволяет произвести количественную оценку этих процессов. Для того, чтобы выявить и количественно оценить причины снижения совершенства процесса и получить информацию о возможности повышения этого совершенства, нужен эксергетический анализ тепловых процессов. Для этого сначала составляют материальный и энергетический балансы, а затем эксергетический. Материальный баланс основан на законе сохранения массы, а энергетический – на законе сохранения энергии. Закона сохранения эксергии не существует, поэтому эксергетический баланс вводится искусственно. Для этого исследуемую систему мысленно отделяют контрольной поверхностью, через которую происходит обмен энергией и веществом с окружающей средой, учитывают в нем внутренние потери эксергии, которые возникают в результате необратимых процессов, протекающих в пределах выделенной системы, и записывают входящие и выходящие потоки эксергии. Общее уравнение эксергетического баланса имеет вид  , (3.32) , (3.32)где Ех1– эксергия веществ, поступающих в систему; Ех2 эксергия веществ, отводимых от системы; ∆Ехи – приращение эксергии системы; 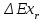 приращение эксергии внешнего источника тепла, участвующего в теплообмене с окружающей средой; приращение эксергии внешнего источника тепла, участвующего в теплообмене с окружающей средой; L – работа, совершаемая системой;  – внутренние потери эксергии в результате необратимости процессов в системе. – внутренние потери эксергии в результате необратимости процессов в системе.При составлении баланса нужно стремиться к возможно более подробной дифференциации потерь эксергии, чтобы получить как можно более подробную информацию о путях повышения совершенства процесса. Подводимые и отводимые потоки эксергии также нужно делить на составляющие. Эксергетический баланс, как и любой другой, можно представить графически, при этом ширина полос будет пропорциональна значениям представляемых величин. Величины, входящие в уравнение эксергетического баланса, могут служить для определения эксергетического КПД. При расчете термического КПД не учитывается различное качество видов энергии. Поэтому термический КПД является показателем, позволяющим сравнивать только однотипные процессы, но не определяет степень совер шенства процесса. При расчете эксергетического КПД как полезный эффект, так и расходы, связанные с проведением процесса, выражаются с помощью эксергии или работы. Благодаря правильной оценке качества различных видов энергии, эксергетический КПД является мерой степени совершенства процесса. Чем меньше необратимость рассматриваемых изменений, тем больше эксергетический КПД. В пределе для идеального обратимого процесса он равен единице, для необратимого – нулю:  , ,где  сумма потоков эксергии, которые определяют получаемый эффект; сумма потоков эксергии, которые определяют получаемый эффект;  сумма потоков эксергии, которые определяют затраты. сумма потоков эксергии, которые определяют затраты.Для реальных процессов 0 <  <1. Сравнивая эксергетический КПД двух однотипных процессов, мы видим, что в процессе с более низким КПД существует возможность увеличения степени совершенства либо путем снижения необратимости в каком-либо звене процесса, либо путем улучшения использования выходящих продуктов. <1. Сравнивая эксергетический КПД двух однотипных процессов, мы видим, что в процессе с более низким КПД существует возможность увеличения степени совершенства либо путем снижения необратимости в каком-либо звене процесса, либо путем улучшения использования выходящих продуктов. Чтобы установить наиболее выгодный путь увеличения совершенства исследуемого процесса, нужно сравнить потери эксергии в отдельных звеньях процесса, а потом изучить возможности уменьшения тех потерь, которые наиболее заметно влияют на совершенство процесса. Например, эксергетический анализ показывает, что эксергетический КПД парового котла даже при самых современных технических решениях очень мал (не превышает 50 %). Вызвано это, прежде всего, необратимостью процесса горения и необратимостью теплообмена между продуктами сгорания и рабочим телом. Это говорит о том, что общий принцип, на котором основан данный тепловой процесс, выбран не наилучшим образом. Нужно менять принцип реализации данного процесса, то есть изменить принцип использования химической энергии топлива. Этот измененный принцип пытаются реализовать в магнито-гидродинамических (МГД) генераторах, в которых происходит непосредственное преобразование химической энергии топлива в электрическую. | ||||||||||