Реферат на тему Законы Фика. реферат. "Законы Фика. Скорость диффузии. Коэффициент диффузии. Примеры."
 Скачать 46.97 Kb.
|
|
Министерство образования и науки Российской Федерации ФГАОУ ВПО “УрФУ имени первого Президента России Б.Н. Ельцина” Кафедра Физической и коллоидной химии Реферат на тему: “Законы Фика. Скорость диффузии. Коэффициент диффузии. Примеры.” Выполнила: Маслова В. А. Руководитель: Маскаева Л. Н. Группа: ФО-210007 Екатеринбург, 2023 Законы Фика. Если в составе молекул вещества имеется примесь молекул другого типа, и эта примесь в объеме распределена неоднородно (например, примесь вводится искусственно в какой-то точке объема), то из-за хаотического движения молекул примесь начнет стремиться к 3 равномерному пространственному распределению. Возникнет перенос вещества примеси – его диффузия. Когда смешиваемые вещества близки (например, отличаются лишь изотопным составом), или когда можно следить за самими молекулами вещества (такие экспериментальные методы сейчас существуют), говорят о самодиффузии. Математическое описание диффузионных процессов было дано в 1855 году Фиком. Он сформулировал два закона основанных на законах теплопроводности: Первый закон Фика: характеризует скорость диффузии атома из одного вещества в другое при постоянном потоке во времени этих атомов и неизменном градиенте их концентрации: Заметим, что для газов и жидкостей молекулярную диффузию следует отличать от процессов конвекции – перемещения макроскопических объемов вещества из-за градиентов давления. Процессы конвекции приводят обычно к гораздо более быстрому распространению примеси вещества в объеме. Будем считать, что конвекция отсутствует, давление и температура везде одинаковы, и рассмотрим в газе случай одномерной диффузии – когда примесь другого вещества распределена неравномерно вдоль некоторой оси х, с концентрацией n(х) – рис. 9.1. Далее, пусть имеет место стационарная ситуация, когда распределение n(х) от времени не зависит. Это означает, что справа имеется источник примесного вещества, а слева – его сток. 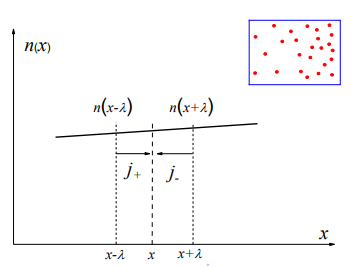 Рис. 9.1. зависимость от координаты х концентрации примеси n(x). Выделим перпендикулярную оси х единичную площадку с некоторой координатой х. Найдем поток молекул через эту площадку. Как уже отмечалось, для газа размер области локального равновесия порядка длины свободного пробега λ. Тогда можно говорить о локальных плотностях примеси в точках с координатами x и x : соответственно о n (x ) и n (x ) . Поток через площадку в газе определяется произведением средней скорости v и локальной плотности, потоки j+ слева в положительном направлении оси х и справа j- в отрицательном направлении этой оси соответственно будут (для потоков используем обозначения в виде строчных букв, чтобы подчеркнуть, что речь идет о движении молекул малых примесей): 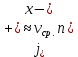 ) ,  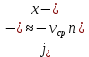.Здесь мы пренебрегаем численным коэффициентом порядка единицы, возникающим из-за того, что молекулы могут достигать площадку под разными углами – см. п. 3.1. Это связано с тем, что для разных углов будет разное значение локальной плотности. Результирующий поток j в направлении оси х есть сумма этих двух потоков: 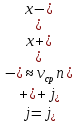 (появляющийся численный коэффициент в виде двойки также здесь опускаем). Мы видим, что диффузионный поток пропорционален градиенту концентрации dn/dx: 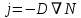 (1)Знак « - » указывает на то, что диффузия идет в сторону уменьшения концентрации N. J – вектор плотности потока атомов вещества, D – коэффициент диффузии, 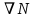 - вектор градиента концентрации диффундирующих атомов.Коэффициент диффузии D – определяет плотность потока атомов вещества при заданном градиенте концентрации [D] =  , так как диффузионный поток атомов перемещается в направлении выравнивания концентрации, коэффициент D является мерой скорости, с которой система способна при условиях выровнять разность концентраций.Эта скорость зависит от подвижности диффундирующих атомов кристаллической решетки полупроводника. Скорость диффузии зависит в общем случае от выбранного кристаллографического направления. Градиент концентрации при объемной диффузии имеет три составляющие по координатным осям, если глубина диффузии значительно меньше поперечных размеров площади, на которой она происходит, то можно принять, что диффузия идет в одном направлении, в этом случае уравнение Фика становится одномерным: 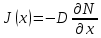 (2)J(x) – плотность потока или число атомов вещества, переносимых в единицу времени через единицу площади; 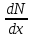 - градиент концентрации диффундирующей примеси в направлении диффузии.Коэффициент диффузии D в газе можно представить также как: 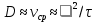 ,Где 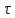 - среднее время между столкновениями.Отметим, что малая концентрация диффундирующей примеси предполагает, что процесс действительно происходит в стационарных условиях, так как при больших концентрациях кроме градиента концентрации возникал бы еще и градиент давления. Однако в случае самодиффузии диффундирующие молекулы могут присутствовать не в виде примеси, а в полностью гомогенной среде. Второй закон Фика: определяет скорость накопления растворимой примеси в любой плоскости перпендикулярной к распространению диффузии. Для одномерного случая второй закон Фика: 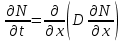 (3)где 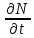 - изменение концентрации диффундирующего вещества во времени.Выражение (3) учитывает возможность зависимости D от концентрации примеси, так как частота обмена местами атомов зависит от структуры полупроводника, если считать, что D=const, то выражение (3) примет вид: 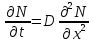 (4)при этом предполагается, что температура диффузионного процесса должна быть постоянной, но если концентрации диффундирующей примеси велики, то D зависит от концентрации и это необходимо учитывать в уравнении (3). Скорость диффузии Диффузия представляет собой физический процесс взаимного проникновения атомов и молекул одного вещества между такими же структурными элементами другого вещества. Итогом этого процесса становится выравнивание уровня концентрации в проникающих соединениях. Скорость диффузии зависит от нескольких факторов: Температуры тела Агрегатного состояния исследуемого вещества В различных газах, где существуют очень большие расстояние между молекулами, скорость диффузии будет самой большой. В жидкостях, где расстояние между молекулами заметно меньше, скорость также уменьшает свои показатели. Самая маленькая скорость диффузии отмечается в твердых телах, поскольку в молекулярных связях наблюдается строгий порядок. Атомы и молекулы сами совершают незначительные колебательные движения на одном месте. Скорость протекания диффузии увеличивается при росте окружающей температуры. Основной формулой скорости диффузии является: 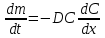 ,Такую формулу представил в виде математического описания Фик. Согласно ей, скорость диффузии прямо пропорциональна градиенту концентрации и площади, через которую осуществляется процесс диффузии. Коэффициент пропорциональности определяет диффузию вещества. Известный физик Альберт Эйнштейн вывел уравнения для коэффициента диффузии: 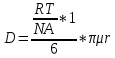 ,Где R – это универсальная газовая постоянная, T – абсолютная температура, r – радиус диффундирующих частиц D – коэффициент диффузии, 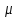 – вязкость средыИз этих уравнений следует, что скорость диффузии будет возрастать: При повышении температуры При повышении градиента концентрации Скорость диффузии уменьшается: При увеличении вязкости растворителя При увеличении размера диффундирующих частиц Если молярная масса увеличивается, тогда коэффициент диффузии уменьшается. В этом случае скорость диффузии также уменьшается. Коэффициент диффузии Коэффициентом диффузии называют физическую величину, которая численно равна количеству диффундирующего вещества, которое проникает за единицу времени через единицу поверхности, если разность плотностей на двух поверхностях, находящихся на расстоянии равном единице длины, равна единице. 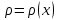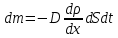Процесс диффузии двухкомпонентной системе для одномерного случая  описывают при помощи закона Фика: (5)Где dm – количество диффундирующего вещества первой составляющей, которая за отрезок времени dt переносится через элементарную площадь dS в направлении нормали x к этой площадке в сторону убыли первого компонента. 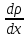 — градиент плотности. D — коэффициент диффузии. Для газов при нормальных условиях коэффициент диффузии лежит внутри интервала: 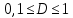 (см2/с). Для жидкостей коэффициент диффузии примерно в 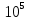 . |