Красители Гуро и Фонга. шухриддин. Закраска методами Гуро и Фонга. Закраска методом Гуро
 Скачать 68.63 Kb. Скачать 68.63 Kb.
|
|
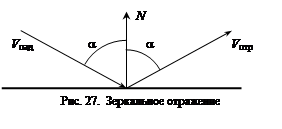
Закраска методами Гуро и Фонга. Закраска методом Гуро. Затенение по Гуро – это метод линейной интерполяции функции освещенности в пределах одной грани. Он был разработан в 1971 и носит имя своего изобретателя. Это простой и эффективный метод придает ощущения изогнутости для ровного полигона. Этот метод также часто используется для со- кращения глубины прорисовываемой сцены путем имитации исчезновения удаленных объектов в тумане. Полигоном в трехмерной графике принято считать участок поверхности, имеющий как минимум три вершины лежащие в одной плоскости. Полигон может иметь произвольное количество вершин, но в трехмерной компьютерной графике в большинстве случаев используют именно треугольные полигоны. Во-первых, три вершины всегда однозначно определяют положение плоскости в пространстве, а четвертая вершина может лежать вне пределов плоскости, и ее положение придется всегда проверять, что вызовет дополнительные трудности. Во-вторых, из треугольников всегда можно получить любой другой многоугольник . Пусть задана плоская грань v1v2v3 (рис.6.1). Найдем значение освещенности в каждой ее вершине, используя формулы 6.1 или 6.2. Обозначим получившиеся значения через I1,I2,I3. Рисуя грань v1v2v3 построчно, будем находить значения освещенности в концах каждого горизонтального отрезка путем линейной интерполяции значений вдоль ребер. Так освещенность в точке А (рис.6.1) вычисляется по следующей формуле: Р 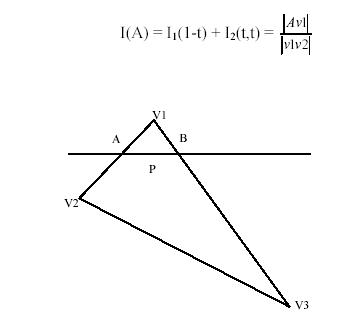 ис. 6.1. Вычисление освещенности в точке A При построении растрового представления отрезка АВ будем считать, что интенсивность пикселей изменяется линейно от I(A) в точке A до I(B) в точке B. Ниже приводится алгоритм, осуществляющий построение горизонтального отрезка с изменением интенсивности от Ia до Ib. 1. Получить координаты точек А и В (xa и xb). 2. Рассчитать по формуле значения интенсивности в этих точках ia и ib. 3. Ввести промежуточное значение интенсивности i и присвоить ему начальное значение равное ia. 4. По формуле приведенной ниже рассчитать приращение интенсивности при переходе из одной точки к другой вдоль оси Х. di = (ib - ia)/(xb – xa + 1) 5. Ввести промежуточное значение х для перехода от точки к точке по оси Х. Присвоить х в качестве начального значения ха. 6. В цикле отрисовать всю линию на каждом шаге наращивая значение х (пока не дойдем до точки хb) и значение i на приращение di, рассчитанное по формуле. Этот алгоритм рассчитан на то, что цветам от ia до ib соответствует набор промежуточных цветов с линейно изменяющейся интенсивностью, например, когда вся палитра состоит из оттенков одного или нескольких цветов. Подобный метод билинейной интерполяции используется в ряде графических систем, например в OpenGL. Метод Гуро гарантирует создание непрерывной функции освещенности вдоль грани объекта, но эта функция не является гладкой (дифференцируемой) на границах граней. Следующий метод строит более гладкую функцию освещенности объекта. Закраска методом Фонга. Аппроксимация Фонга, или затенение по Фонгу , носят название по имени своего изобретателя - Ву Тонг Фонга. Этот метод дает более точные результаты при затенении многоугольников по сравнению с затенением Гуро. Суть алгоритма Фонга заключается в определении нормали к поверхности в каждой вершине многоугольника и последующей интерполяции вектора по всему полигону поверхности. Далее для каждого пикселя необходимо вычислить значение яркости, основываясь на значениях вектора нормали в этом пикселе. Этот процесс требует больше времени, чем вышеописанные методы, и его программная реализация плохо подходит для использования в играх, рассчитанных на домашний компьютер. Поэтому большинство компьютерных программ используют значительно упрощенный вариант аппроксимаций. Затенение по Фонгу – это достаточно популярный метод для реализации затенения, особенно в программе 3D Studio. Однако, несмотря на то, что этот метод значительно точнее затенения Гуро, он по-прежнему не является физически точным. Затенение по Фонгу – это приближенная реализация физической модели света. Каждый одиночный пиксел имеет собственное значение яркости, просчитанное при использовании интерполированного вектора нормали. Просчет затенения по Фонгу включает вычисление двух квадратных корней, реализацию двух операций деления, четырех операций умножения. Кроме этого используется значительное количество операций сложения для каждого пикселя, а алгоритм не является целочисленным. Р 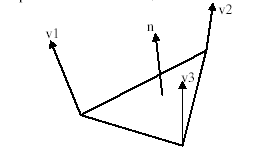 ис. 6.2. Вычисление вектора нормали во внутренней точке Затенение по Фонгу основывается на том, что количество света, отраженного от поверхности прямо пропорционально косинусу угла между нормалью к поверхности и направлением света. При этом не имеет значения, под каким углом вы смотрите на поверхность. Реально очень немногие поверхности обладают такими идеальными свойствами. Наиболее подходящими являются поверхности, имеющие микроскопические шероховатости, например, хорошо отшлифованное дерево. Большинство поверхностей также обладают некоторой степенью спектрального отражения. Затенение по Фонгу не разделяет их между собой. Оно также не учитывает тот факт, что яркость обратно пропорциональна квадрату расстояния от источника света. Рассмотрим полигон. В каждой вершине полигона мы имеем вектор нормали к поверхности, частью которой полигон является (v1, v2, v3). Эти векторы интерполированы по всей площади полигона, подобно тому, как это делалось для затенения Гуро. В затенении Гуро, однако, используется только одно значение -shade (это скалярная величина). Здесь же оперируем вектором с тремя значениями Vx, Vy и Vz (три значения, три координаты – определяющие положение вектора в пространстве). Возьмем пиксель на этом полигоне (рис. 6.2). Вектор нормали, соответствующий этому пикселю на поверхности равен n. Луч падает на полигон вдоль вектора l. Количество света, отраженного от данного пикселя, является функцией скалярного произведения векторов, дающих в результате число, определяющее длину результирующего вектора. Скалярное произведение вектора n(x,y,z) и вектора l(x,y,z) может производиться по любой из двух формул: n*l = nxlx + nyly + nzlz n*l = |n|*|l| cosθ , где θ (тетта) - угол между векторами. Нам больше подходит второй вариант, т.к. он оперирует с длинами (величинами) векторов и углом между ними. Величина нормали к поверхности равна 1. А величина вектора падающего света приводится к 1 и будет иметь значения от 0 до 1. Значение 1 соответствует самому яркому свету. Далее результатом вычисления данной функции будет значение в диапазоне от -1 до 1, где 1 соответствует максимальной яркости. Понятия отрицательного света не существует, поэтому значения меньше 0 следует заменять на 0. Если затем умножить данное значение на величину яркости света (brightness), то получаем значение яркости рассматриваемого пикселя. Методы Гуро и Фонга для закрашивания поверхностей. Методы прямой и обратной трассировки лучей Закрашивание поверхностей Рассмотрим методы закрашивания объектов, моделируемых многогранниками и полигональными сетками. Они основаны на моделях отражения света. Зеркальное отражение. Угол между нормалью и падающим лучом равен углу между нормалью и отраженным лучом. Оба луча и нормаль располагаются в одной плоскости (рис. 27). Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственного цвета такая поверхность не имеет. Световая энергия падающего
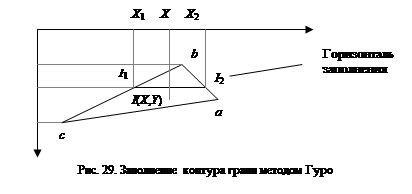
луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеяние не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0,5 мкм. Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны: чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие. При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов падения луча, близких к 90°. Рекомендуемые материалы Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos a)p, где a – угол отклонения от линии идеально отраженного луча. Показатель p находится в диапазоне от 1 до 200 и зависит от качества полировки. Соотношение можно записать следующим образом: Is = I Ks cos pa, где I – интенсивность излучения источника; Ks – коэффициент пропорциональности. Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности: Id = I Kd cos q, где I – интенсивность источника света; Kd – коэффициент, который учитывает свойства материала поверхности. Значение Kd находится в диапазоне от 0 до 1. Интенсивность отраженного света не зависит от расположения наблюдателя. Матовая поверхность имеет свой цвет. Наблюдаемый цвет определяется комбинацией собственного цвета поверхности и цвета излучения источника света. Поскольку в природе не существует идеально зеркальных или полностью матовых поверхностей, то при изображении объектов средствами КГ обычно моделируют сочетание зеркального и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузного и зеркального компонентов: Iотр = I (Kd cos q + Ks cos pa), где константы Kd, Ks определяют отражательные свойства материала. Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов q и a. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой: Iотр = Ia Ka + I (Kd cos q + Ks cos pa), где Ia – интенсивность рассеянного света, Ka – константа, определяющая рассеиваюшие свойства поверхности. Следует учесть тот факт, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использования такого правила вызывает определенные сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой Iотр = Ia Ka + I (Kd cos q + Ks cos pa)/(R + k), где R – расстояние от центра проекции до поверхности, k – константа, подбираемая эмпирически. Определение цвета закрашивания точек объектов в соответствии с описанной моделью. Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонентов. Коэффициенты Ka и Kd различны – они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент Ks будет одинаковым для всех компонентов цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонентов. Метод Гуро Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения числа граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней – такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить число граней, что приводит к существенному замедлению визуализации – чем больше граней, тем меньше скорость рисования объектов. Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа. 1. Вычисляются нормали к каждой грани. 2. Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 28). 3. На основе нормалей в вершинах вычисляются значения интенсивности в вершинах согласно выбранной модели отражения света. 4. 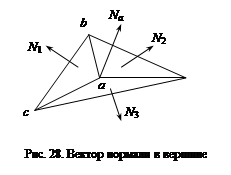 Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах. Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.Вектор нормали в вершине (a) равен: Na = (N1 + N2 + N3) / 3. Интерполированные значения интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно определять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 29).
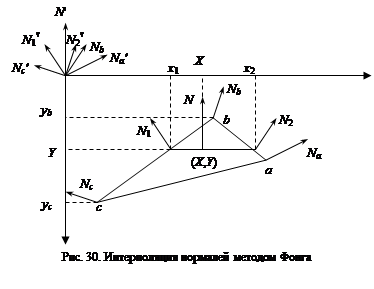
Интерполированная интенсивность I в точке (X, Y) определяется исходя из пропорции (I - I1) / (X - X1) = (I2 - I1) / (X2 - X1). Отсюда I = I1 + (I2 - I1) (X - X1) / (X2 - X1). Значения интенсивностей I1 и I2 на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах: (I1 - Ib) / (Y - Yb) = (Ic - Ib) / (Yc - Yb) (I2 - Ib) / (Y - Yb) = (Ia - Ib) / (Ya - Yb) или I1 = Ib + (Ic - Ib) (Y - Yb) / (Yc - Yb) I2 = Ib + (Ia - Ib) (Y - Yb) / (Ya - Yb) Метод Фонга Метод Фонга аналогичен методу Гуро, но при его использовании для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей (рис. 30).
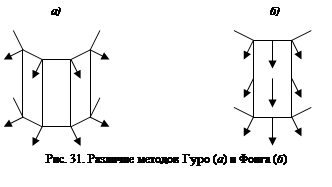
1. Определяются нормали к граням. 2. По нормалям к граням определяются нормали в вершинах. 3. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали. 4. По направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света. Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'a, N'b и N'c, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям Na, Nb и Nc в вершинах a, b и c. Сначала найдем N'1 и N'2: 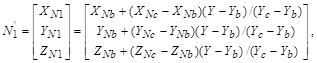 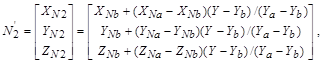 где XNa, YNa, ZNa, XNb, YNb, ZNb, XNc, YNc, ZNc – координаты векторов N'a, N'b и N'c. Теперь найдем координаты вектора N': 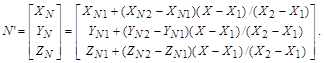 Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N. Метод Фонга сложнее метода Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций (рис. 31). Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркаль
ных поверхностей. Методы трассировки лучей Прямая трассировка. В методе прямой трассировки генерируется пучок лучей, выходящих из источника во всевозможных направлениях. Большинство лучей, испущенных источником, не попадает в приемник, а значит, и не влияет на формируемое в нем изображение. Лишь очень малая часть лучей после всех отражений и преломлений в конце концов попадает в приемник, создавая изображение сцены в его рецепторах. На шероховатых поверхностях возникает множество диффузно отраженных лучей. Все их нужно программно генерировать и отслеживать, что лавинообразно усложняет задачу трассировки. Прохождение луча в неидеальной среде сопровождается рассеянием и поглощением световой энергии на ее микрочастицах. Эти физические процессы чрезвычайно трудно адекватно моделировать на ЭВМ с ее конечными вычислительными ресурсами. На практике ограничиваются применением коэффициента затухания энергии луча на единицу пройденного им расстояния. Аналогично вводятся коэффициенты уменьшения энергии луча при его отражении и преломлении на поверхности раздела сред. С учетом этих коэффициентов отслеживается уменьшение энергии всех первичных и вторичных лучей в процессе их блуждания в пространстве сцены. Как только энергия некоторого луча становится меньше заданного абсолютного уровня или уменьшается в заданное число раз, трассировка данного луча прекращается. Таким образом, главными недостатками метода прямой трассировки являются его большая трудоемкость и малая эффективность. При реализации метода большая часть работы по расчету пересечений лучей с объектами оказывается проделанной впустую. Обратная трассировка. Метод обратной трассировки разработан в 80-х годах. Основополагающими считаются работы Уиттеда и Кея. Для отсекания лучей, не попавших в приемник, достаточно рассматривать наблюдателя в качестве источника обратных лучей. Первичным лучом будет считаться луч V от наблюдателя к какой-либо точке на поверхности объекта. По рассмотренным выше методикам рассчитываются вторичные, третичные и т.д. лучи. В результате для каждого первичного луча строится дерево трассировки, ветви которого составляют вторичные лучи. Ветвление трассы заканчивается, если: ● луч выходит за пределы сцены, ● луч встречается с непрозрачным телом, поглощающим свет, ● луч попадает в источник света, ● интенсивность луча падает ниже порога чувствительности, ● число расщеплений первичного луча становится слишком большим для имеющихся машинных ресурсов. Результирующая прямая световая энергия (цвет и интенсивность), попавшая в приемник из направления V, слагается из энергий терминальных вершин дерева с учетом их потерь при распространении в оптических средах. Метод обратной трассировки фактически аккумулирует все лучи, в действительности приходящие в приемник из определенного направления независимо от их начала. Это позволяет видеть и изображать на экране: ● непрозрачные объекты, поглощающие обратные лучи; ● прозрачные объекты, через которые благодаря преломлению наблюдателю видны другие объекты; ● отражения объектов на зеркальных поверхностях, в том числе и блики, соответствующие попаданию обратных лучей в источник света; ● тени, образующиеся в точках поверхности, заслоненных от источника другими объектами; ● другие разнообразные оптические эффекты. Количество "зондирующих" обратных лучей, подвергаемых трассировке, ограничено числом точек на поверхностях объектов сцены, видимых из точки расположения наблюдателя и перебираемых с конечным шагом, зависящим от разрешения экрана. Благодаря этому объем вычислительных затрат в методе обратной трассировки существенно уменьшается по сравнению с методом прямой трассировки. Возможно комбинирование обоих методов для оптимизации алгоритмов и снижения их трудоемкости. Алгоритмы трассировки носят характер рекурсивной процедуры, которая вызывает саму себя при появлении вторичного луча (анализируемый луч отражается или преломляется). Большая часть вычислений при реализации методов трассировки приходится на расчет пересечений лучей с поверхностями, в связи с чем они применяются для изображения оптических эффектов в сценах с небольшим числом объектов. При практической реализации метода обратной трассировки вводят нижеприведенные ограничения. Некоторые из них необходимы, чтобы можно было в принципе решить задачу синтеза изображения, а некоторые ограничения позволяют значительно повысить быстродействие трассировки. Ограничения метода обратной трассировки: 1. Среди всех типов объектов выделим источники света. Они могут только излучать свет, но не могут его отражать или преломлять. Обычно рассматриваются точечные источники. 2. Свойства отражающих поверхностей описываются суммой двух компонентов: диффузного и зеркального. 3. Зеркальность, в свою очередь, также описывается двумя составляющими. Первая (reflection) учитывает отражение от других объектов, не являющихся источниками света. Строится только один зеркально отраженный луч r для дальнейшей трассировки. Вторая компонента (specular) означает световые блики от источников света. Для этого направляются лучи на все источники определяются углы, образуемые этими лучами с зеркально отраженным лучом обратной трассировки (r). При зеркальном отражении цвет точки поверхности определяется цветом того, что отражается. В простейшем случае зеркало не имеет собственного цвета поверхности. 4. При диффузном отражении учитываются только лучи от источников света. Лучи от зеркально отражающих поверхностей игнорируются. Если луч, направленный на данный источник света, закрывается другим объектом, значит, данная точка объекта находится в тени. При диффузном отражении цвет освещенной точки поверхности определяется собственным цветом поверхности и цветом источников света. 5. Для прозрачных (transparent) объектов обычно не учитывается зависимость коэффициента преломления от длины волны. Иногда прозрачность вообще моделируют без преломления, т.е. направление преломленного луча t совпадает с направлением падающего луча. 6. Для учета освещенности объектов светом, рассеиваемым другими объектами, вводится фоновая составляющая (ambient). 7. Для завершения трассировки вводят некоторое пороговое значение освещенности, которое уже не должно вносить вклад в результирующий цвет, либо ограничивают число итераций. Положительные черты метода обратной трассировки: ● универсальность, применимость для синтеза изображений достаточно сложных пространственных сцен. Воплощает многие законы оптики. Просто реализуются разнообразные проекции; ● даже усеченные варианты данного метода позволяют получить достаточно реалистичные изображения. Например, если ограничиться только первичными лучами (из точки проецирования), то это дает удаление невидимых точек. Трассировка уже одного-двух вторичных лучей дает тени, зеркальность, прозрачность; |