Метод Монте-Карло. Замечания руководителя Содержание
 Скачать 64.6 Kb. Скачать 64.6 Kb.
|
Замечания руководителяСодержаниеЗамечания руководителя 3 1 Общая характеристика работы. 5 1.2 Актуальность работы. 5 2 Цель и задачи работы. 6 3 Метод Монте-Карло. 7 3.1 Сущность метода Монте-Карло. 7 3.2 Оценка погрешности метода Монте—Карло 9 3.3 Случайные числа 11 3.4 Разыгрывание дискретной случайной величины 12 3.5 Разыгрывание противоположных событий 14 3.6 Разыгрывание полной группы событий 15 4 Информационная безопасность и метод Монте-Карло. 16 5 Заключение 28 6 Список информационных источников. 29 1 Общая характеристика работы.1.2 Актуальность работы.При расчете систем с отказами крайне важно использовать тот метод моделирования системы, который наиболее точно может описать данную систему. Метод Монте-Карло уже давно применяется для расчета экономических рисков, но его функциональные возможности могут позволить рассчитывать и риски в современных информационных системах. Хотя данный метод почти и не применяется при расчете рисков, он имеет большую значимость при описании систем. Применимость данного метода к системам с отказами крайне сближает его с информационными системами, где данный критерий имеет не последнюю роль в жизнедеятельности системы. Поэтому крайне важно адаптировать метод Монте-Карло применительно к рискам информационной безопасности. 2 Цель и задачи работы.Цель данной работы заключается в изучении метода имитационного моделирования Монте-Карло и получении практических навыков по применению данного метода для расчета систем массового обслуживания с отказами. Из поставленной цели, задачами данной работы следующие: Рассмотреть общие принципы метода Монте-Карло Применить метод Монте-Карло применительно к информационной безопасности. Рассчитать систему массового обслуживания с отказами методом Монте-Карло. Разработать код приложения реализующего метод Монте-Карло. 3 Метод Монте-Карло.3.1 Сущность метода Монте-Карло.ЭВМ позволяют легко получать так называемые псевдослучайные числа (при решении задач их применяют вместо случайных чисел); это привело к широкому внедрению метода Монте-Карло во многие области науки и техники (статистическая физика, теория массового обслуживания, теория игр и др.). Данный метод используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т. д.). Сущность метода Монте—Карло состоит в следующем: требуется найти значение 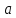 некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно 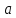 : :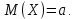 Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое 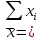 )/n )/nи принимают х в качестве оценки (приближенного значения) a* искомого числа 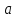 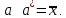 Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину X, как найти ее возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания 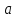 его оценкой его оценкой 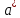 . .Отыскание возможных значений случайной величины X (моделирование) называют «разыгрыванием случайной величины». 3.2 Оценка погрешности метода Монте—КарлоПусть для получения оценки a* математического ожидания a случайной величины X было произведено n независимых испытаний (разыграно n возможных значений X) и по ним была найдена выборочная средняя х, которая принята в качестве искомой оценки: а* = х. Ясно, что если повторить опыт, то будут получены другие возможные значения X, следовательно, другая средняя, а значит, и другая оценка а*. Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно, возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы 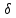 допускаемой ошибки с заданной вероятностью (надежностью) допускаемой ошибки с заданной вероятностью (надежностью) 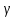 : :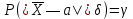 Интересующая нас верхняя граница ошибки б есть не что иное, как «точность оценки» математического ожидания по выборочной средней при помощи доверительных интервалов. Рассмотрим следующие три случая. Случайная величина X распределена нормально и ее среднее квадратическое отклонение 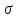 известно. В этом случае с надежностью известно. В этом случае с надежностью 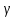 верхняя граница ошибки: верхняя граница ошибки: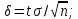 (*) (*)где n—число испытаний (разыгранных значений X); t — значение аргумента функции Лапласа, при котором Ф(t) = 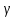 /2, /2, 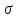 — известное среднее квадратическое отклонение X. — известное среднее квадратическое отклонение X.Случайная величина X распределена нормально, причем ее среднее квадратическое отклонение 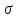 неизвестно. В этом случае с надежностью неизвестно. В этом случае с надежностью 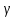 верхняя граница ошибки: верхняя граница ошибки: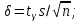 (**) (**)где n — число испытаний; s—«исправленное» среднее квадратическое отклонение, 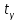 – табличное значение. – табличное значение.Случайная величина X распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (n>30) с надежностью, приближенно равной 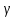 , верхняя граница ошибки может быть вычислена по формуле (*), если среднее квадратическое отклонение , верхняя граница ошибки может быть вычислена по формуле (*), если среднее квадратическое отклонение 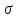 случайной величины X известно; если же случайной величины X известно; если же 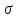 неизвестно, то можно подставить в формулу (*) его оценку s—«исправленное» среднее квадратическое отклонение либо воспользоваться формулой (**). Заметим, что чем больше n, тем меньше различие между результатами, которые дают обе формулы. Это объясняется тем, что при неизвестно, то можно подставить в формулу (*) его оценку s—«исправленное» среднее квадратическое отклонение либо воспользоваться формулой (**). Заметим, что чем больше n, тем меньше различие между результатами, которые дают обе формулы. Это объясняется тем, что при 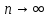 распределение Стьюдента стремится к нормальному. распределение Стьюдента стремится к нормальному. Замечание. Для того чтобы найти наименьшее число испытаний, которые обеспечат наперед заданную верхнюю границу ошибки 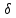 , надо выразить n из формул (*) и (**): , надо выразить n из формул (*) и (**):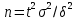 , , 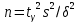 . .3.3 Случайные числаРанее было указано, что метод Монте—Карло основан на применении случайных чисел; дадим определение этих чисел. Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0, 1). Случайными числами называют возможные значения г непрерывной случайной величины R, распределенной равномерно в интервале (0, 1). В действительности пользуются не равномерно распределенной случайной величиной R, возможные значения которой, вообще говоря, имеют бесконечное число десятичных знаков, а квазиравномерной случайной величиной R*, возможные значения которой имеют конечное число знаков. В результате замены R на R* разыгрываемая величина имеет не точно, а приближенно заданное распределение. 3.4 Разыгрывание дискретной случайной величиныПусть требуется разыграть дискретную случайную величину X, т. е. получить последовательность ее возможных значений 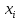 (i= 1, 2, .... n), зная закон распределения X: (i= 1, 2, .... n), зная закон распределения X: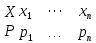 Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0, 1), а через 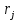 (j=1, 2, ...) — ее возможные значения, т. е. случайные числа. (j=1, 2, ...) — ее возможные значения, т. е. случайные числа.Разобьем интервал 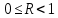 на оси Or точками с координатами на оси Or точками с координатами 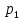 , , 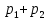 , … , , … , 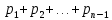 на n частичных интервалов на n частичных интервалов 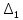 , ,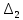 ,…, ,…, 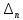 : :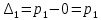 , ,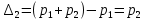 , ,… 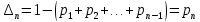 . .Видно, что длина частичного интервала с индексом i равна вероятности с тем же индексом: 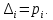 Теорема. Если каждому случайному числу 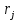 (0 ≤ (0 ≤ 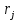 < 1), которое попало в интервал < 1), которое попало в интервал 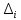 , ставить в соответствие возможное значение , ставить в соответствие возможное значение 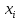 , то разыгрываемая величина будет иметь заданный закон распределения: , то разыгрываемая величина будет иметь заданный закон распределения: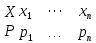 Доказательство. Так как при попадании случайного числа 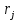 в частичный интервал в частичный интервал 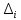 разыгрываемая величина принимает возможное значение разыгрываемая величина принимает возможное значение 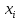 , а таких интервалов всего n, то разыгрываемая величина имеет те же возможные значения, что и X, а именно , а таких интервалов всего n, то разыгрываемая величина имеет те же возможные значения, что и X, а именно 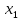 , ... , , ... , 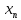 . .Вероятность попадания случайной величины R в интервал 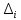 равна его длине, а в силу (*) для равна его длине, а в силу (*) для 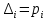 . Таким образом, вероятность попадания R в интервал . Таким образом, вероятность попадания R в интервал 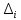 , равна , равна 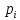 . Следовательно, вероятность того, что разыгрываемая величина примет возможное значение . Следовательно, вероятность того, что разыгрываемая величина примет возможное значение 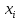 также равна также равна 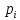 (поскольку в случае попадания случайного числа (поскольку в случае попадания случайного числа 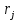 в интервал в интервал 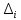 разыгрываемая величина принимает возможное значение разыгрываемая величина принимает возможное значение 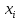 ,). Итак, разыгрываемая величина имеет заданный закон распределения. ,). Итак, разыгрываемая величина имеет заданный закон распределения.Правило. Для того чтобы разыграть дискретную случайную величину, заданную законом распределения 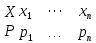 надо: 1) разбить интервал (0, 1) оси Or на n частичных интервалов: 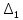 — (0; — (0; 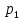 ), ), 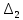 — ( — (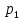 ; ; 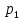 + +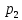 ), … , ), … , 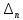 — ( — (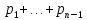 ; ; 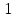 ); );2) выбрать (например, из таблицы случайных чисел) случайное число 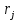 . .Если 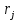 попало в частичный интервал попало в частичный интервал 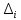 , то разыгрываемая дискретная случайная величина приняла возможное значение , то разыгрываемая дискретная случайная величина приняла возможное значение 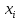 . .3.5 Разыгрывание противоположных событийПусть требуется разыграть испытания, в каждом из которых событие А появляется с известной вероятностью р и, следовательно, не появляется с вероятностью q = 1 - р. Введем в рассмотрение дискретную случайную величину X с двумя возможными значениями (для определенности примем 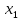 =1, =1, 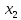 = 0) и соответствующими им вероятностями = 0) и соответствующими им вероятностями 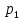 — р, — р, 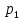 = q. Условимся считать, что если в испытании величина X приняла возможное значение = q. Условимся считать, что если в испытании величина X приняла возможное значение 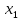 =1, то событие А наступило; если X = =1, то событие А наступило; если X =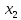 = 0, то событие А не наступило, т. е. появилось противоположное событие = 0, то событие А не наступило, т. е. появилось противоположное событие 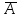 . .Таким образом, разыгрывание противоположных событий А и 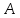 сведено к разыгрыванию дискретной случайной величины X с заданным законом распределения: сведено к разыгрыванию дискретной случайной величины X с заданным законом распределения: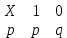 Для разыгрывания X надо интервал (0, 1) разбить точкой р на два частичных интервала: 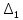 — (0, р) и — (0, р) и 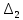 — (р, 1). Затем выбирают случайное число — (р, 1). Затем выбирают случайное число 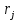 . Если . Если 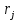 попадает в интервал попадает в интервал 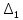 , то X — , то X — 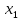 (наступило событие A); если (наступило событие A); если 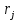 попадает в интервал попадает в интервал 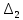 , то Х = , то Х =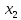 = 0 (событие А не наступило). = 0 (событие А не наступило).Правило. Для того чтобы разыграть испытания, в каждом из которых вероятность появления события равна р и, следовательно, вероятность наступления противоположного события А равна 1—р, надо выбрать (например, из таблицы случайных чисел) случайное число 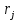 (j=1, 2, ...); если (j=1, 2, ...); если 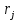 < р, то событие А наступило; если < р, то событие А наступило; если 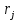 ≥ р, то появилось противоположное событие А. ≥ р, то появилось противоположное событие А.3.6 Разыгрывание полной группы событийРазыгрывание полной группы n (n > 2) несовместных событий 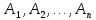 , вероятности которых , вероятности которых 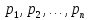 известны, можно свести к разыгрыванию дискретной случайной величины X со следующим законом распределения (для определенности примем известны, можно свести к разыгрыванию дискретной случайной величины X со следующим законом распределения (для определенности примем 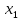 = 1, = 1, 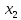 = 2, ...., = 2, ...., 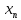 = n): = n):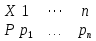 Действительно, достаточно считать, что если в испытании величина X приняла значение 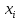 = i(i — 1, 2, ..., n), то наступило событие = i(i — 1, 2, ..., n), то наступило событие 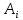 . Справедливость этого утверждения следует из того, что число n возможных значений X равно числу событий полной группы и вероятности возможных значений . Справедливость этого утверждения следует из того, что число n возможных значений X равно числу событий полной группы и вероятности возможных значений 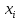 и соответствующих им событий и соответствующих им событий 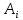 одинаковы: Р(Х = одинаковы: Р(Х = 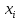 ) = P( ) = P(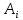 )= )=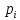 . Таким образом, появление в испытании события А равносильно событию, состоящему в том, что дискретная случайная величина X приняла возможное значение . Таким образом, появление в испытании события А равносильно событию, состоящему в том, что дискретная случайная величина X приняла возможное значение 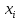 . .Правило. Для того чтобы разыграть испытания, в каждом из которых наступает одно из событий 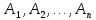 полной группы, вероятности которых полной группы, вероятности которых 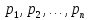 известны, достаточно разыграть дискретную случайную величину X со следующим законом распределения: известны, достаточно разыграть дискретную случайную величину X со следующим законом распределения: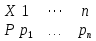 Если в испытании величина X приняла возможное значение 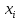 = i, то наступило событие = i, то наступило событие 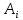 . .4 Информационная безопасность и метод Монте-Карло.Как известно в экономике, как и во многих других науках, используется имитационное моделирование. Одним из используемых методов является метод “Монте-Карло”. В общем случае имитационное моделирование Монте-Карло – это процедура, с помощью которой математическая модель определения какого-либо финансового показателя подвергается ряду имитационных прогонов с помощью компьютера. В ходе процесса имитации строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами. Процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Результаты имитации собираются и анализируются статистически, с тем, чтобы оценить меру риска. Возможности этого метода не должны ограничиваться только экономической сферой. Благодаря использованию случайных сценариев и величин он так же может быть использован в проектировании систем безопасности всевозможных компьютеризированных систем от внешних и внутренних атак. Метод имитационного моделирования Монте-Карло создает дополнительную возможность при оценке риска за счет того, что делает возможным создание случайных сценариев. Применение анализа риска использует богатство информации, будь она в форме объективных данных или оценок экспертов, для количественного описания неопределенности, существующей в отношении основных переменных проекта и для обоснованных расчетов возможного воздействия неопределенности на эффективность проекта. Результат анализа риска выражается не каким-либо единственным значением показателя защищенности, а в виде вероятностного распределения возможных значений этого показателя. Следовательно, потенциальный заказчик системы, с помощью метода Монте-Карло будет обеспечен полным набором данных, характеризующих риски проекта. На этой основе он сможет принять взвешенное решение об использовании именно ее. Процесс анализа риска может быть разбит на следующие стадии. Прогнозная модель; Подготовка модели, способной прогнозировать расчет эффективности проекта; Распределение вероятности (шаг 1); Определение вероятностного закона распределения случайных переменных; Распределение вероятности (шаг 2); Установление границ диапазона значений переменных; Условия корреляции; Установление отношений коррелированных переменных; Имитационные прогоны; Генерирование случайных сценариев, основанных на наборе допущений; Анализ результатов; Статистический анализ результатов имитации; Процесс анализа риска. Таким образом, данный метод является универсальным и довольно эффективным для решения задач и статистического анализа в системах, оперирующих случайными величинами (в случае защиты систем зачастую имеются лишь вероятности развития тех или иных сценариев). Поэтому и должны рассматриваться возможности его применения не только в экономической практике, но и в сфере компьютерной и сетевой безопасности. 5. Практическая часть Оценим надежность простейшей системы методом Монте-Карло. Условие: Система состоит из трех блоков, соединенных последовательно. Первый блок содержит 2 элемента: A, B. Второй блок содержит 3 элемента: C, D, E. Третий блок содержит 1 элемент: F. а) Найти оценку P* надежности системы, зная вероятность безотказной работы P(A) = 0,8, P(B) = 0,9, P(C) = 0,7, P(D) = (0,75), P(E) = 0,75, P(F) = 0,6 б) Найти абсолютную погрешность 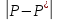 , где P – надежность системы вычисленная аналитически. Произвести 30 испытаний. , где P – надежность системы вычисленная аналитически. Произвести 30 испытаний.Решение: Выберем из таблицы приложения 9 случайные числа. Если случайное число меньше вероятности события, то событие наступило и наоборот. Разыграем события A, B, C, D, E, F, состоящие в безотказной работе соответственно элементов A, B, C, D, E, F. Результаты испытания буду записывать в таблицу 1.
Произведя 30 испытаний, получу, что в 15 из них система работала безотказно. В качестве оценки искомой надежности P приму относительную частоту P*=15/30=0,5 Далее найду надежность системы P аналитически. Вероятности безотказной работы первого, второго и третьего блоков равны: 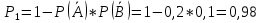 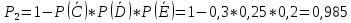 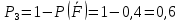 Вероятность безотказной работы системы будет равно 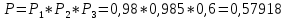 Вычислю абсолютную погрешность 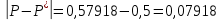 5 ЗаключениеВ ходе выполнения данной курсовой работы был изучен метод имитационного моделирования Монте-Карло, рассчитана система массового обслуживания с отказами, имеющая три узла, и разработан код программы, реализующий метод Монте-Карло для расчета данных систем. В практической части для системы были получены значения оценки вероятности безотказной работы устройства за время длительностью 6 часов и среднее время безотказной работы устройства. Данные полученные программой и найденные эмпирическим путем совпадают, учитывая погрешность. 6 Список информационных источников.Таха Х.А. Введение в исследование операций (6-е издание, 2001). Кремер Н.Ш. (ред.)_Исследование операций в экономике(2005). Гмурман В.Е Теория вероятностей и математическая статистика 2003 -479с. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (3-е издание, 1979). Бэрон Шварц, MySQL. Оптимизация производительности, 2010 год. Джеймс Р. Грофф, Пол Н. Вайнберг, SQL: Полное руководство, 2001 год. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
