Замечательные точки математики. Замечательные точки треугольника. Замечательные точки треугольника Теория Теорема 1
 Скачать 265.77 Kb. Скачать 265.77 Kb.
|
|
Замечательные точки треугольника Теория: Теорема 1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Теорема 2. ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла. 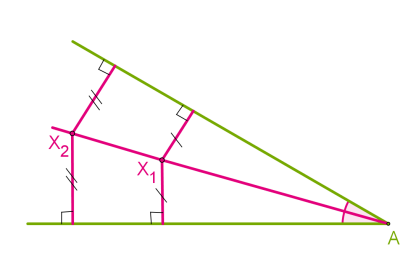 Теорема 3. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. Теорема 4. (обратная) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. 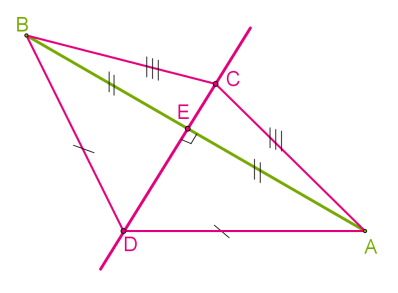 Первая замечательная точка треугольника — точка пересечения биссектрис Теорема 5. Биссектрисы треугольника пересекаются в одной точке. 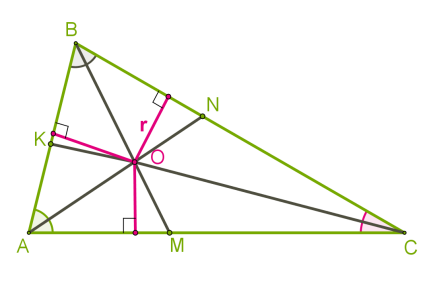 AN, BM — биссектрисы, O — точка их пересечения. Является ли биссектрисой CK? Если точка O равноудалена от сторон AB и AC и от сторон BA и BC, то она лежит на биссектрисе угла ∡C, так как равноудалена от сторон угла. Эта точка и есть центр вписанной в треугольник окружности, всегда находится в треугольнике. Вторая замечательная точка треугольника — точка пересечения серединных перпендикуляров сторон треугольника Теорема 6. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.  Допустим, точка O — точка пересечения двух серединных перпендикулярах сторон AB и BC. Она равноудалена от точек A и B, и от точек B и C. Следовательно, она лежит на серединном перпендикуляре стороны AC, так как равноудалена от её конечных точек. Эта точка и есть центр описанной около треугольника окружности, находится в треугольниках с острыми углами, вне треугольника с тупым углом и на гипотенузе прямоугольного треугольника. Третья замечательная точка треугольника — точка пересечения медиан Теорема 7. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.  Точка пересечения медиан является центром тяжести треугольника. Четвёртая замечательная точка треугольника — точка пересечения высот треугольника Теорема 8. Высоты треугольника или их продолжения пересекаются в одной точке. 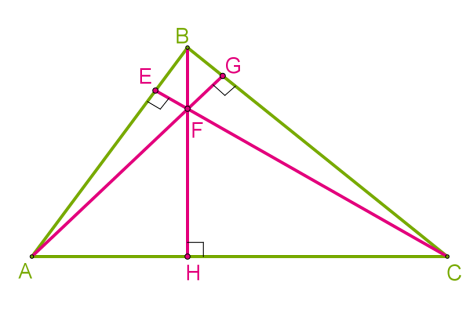  Точку пересечения высот называется ортоцентром треугольника. В 1765 году немецкий математик Эйлер доказал, что в любом треугольнике ортоцентр, центр тяжести и центр описанной окружности лежат на одной прямой, названой позже прямой Эйлера.  В двадцатых годах XIX века французские математики Понселе, Брианшон и другие установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же окружности. 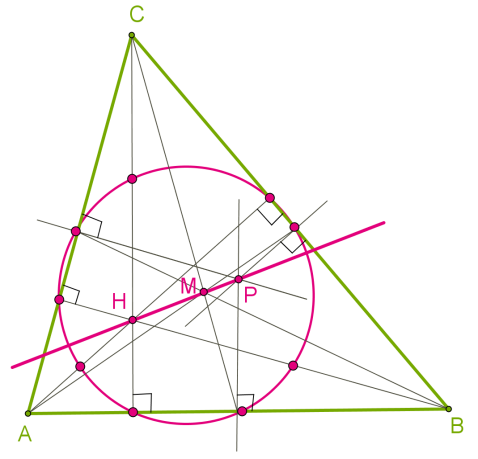 |
