Высшмат. Решение Белоусов. Решение. У равнение прямой, проходящей через точкиАиВ запишется в виде
 Скачать 140.38 Kb. Скачать 140.38 Kb.
|
|
Задание 1. Решение. Уравнение прямой, проходящей через точки А и В запишется в виде 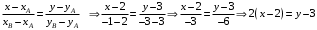 Уравнение прямой 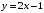 . Найдём точку пересечения этой прямой с осью абсцисс . Найдём точку пересечения этой прямой с осью абсцисс . .Прямая пересекает ось абсцисс в точке 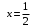 . .Ответ 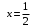 Задание 2. Вершины треугольника А(3,-3), В(5,-1). Точка пересечения высот из этих вершин N(4, 3). Найти площадь треугольника. Решение. Сделаем схематический чертёж.  Высота АЕ проходит через точки А и N, её уравнение 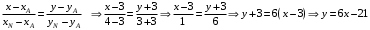 Угловой коэффициент прямой 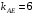 , сторона ВС , сторона ВС 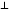 АЕ, следовательно, угловой коэффициент прямой ВС равен АЕ, следовательно, угловой коэффициент прямой ВС равен 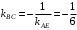 . Запишем уравнение стороны ВС . Запишем уравнение стороны ВС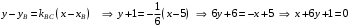 Высота ВD проходит через точки В и N, её уравнение 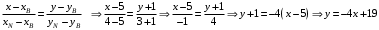 Угловой коэффициент прямой 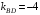 , сторона АС , сторона АС 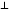 ВD, следовательно, угловой коэффициент прямой АС равен ВD, следовательно, угловой коэффициент прямой АС равен 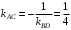 . Запишем уравнение стороны АС . Запишем уравнение стороны АС . .Стороны АС и ВС пересекаются в точке С, найдём координаты точки С из системы уравнений: 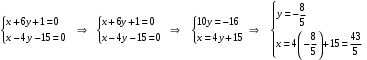 Координаты точки Координаты точки 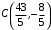 . Известны все три вершины треугольника, площадь треугольника найдём по формуле . Известны все три вершины треугольника, площадь треугольника найдём по формуле 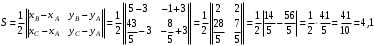 Ответ 4,1 кв. ед. Задание 3. Найти каноническое уравнение эллипса по следующим данным: эксцентристет равен 0,6; расстояние между фокусами 6. Решение. Каноническое уравнение эллипса имеет вид 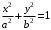 , ,где  и и 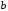 полуоси эллипса. Расстояние между фокусами равно полуоси эллипса. Расстояние между фокусами равно 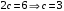 . .Полуось  -большая, -большая,  , тогда эксцентриситет равен , тогда эксцентриситет равен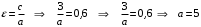 Найдём  Нашли каноническое уравнение 1-ого эллипса 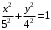 Полуось 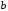 -большая, -большая, 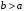 , тогда эксцентриситет равен , тогда эксцентриситет равен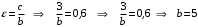 Найдём 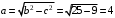 Нашли каноническое уравнение 2-ого эллипса 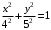 Ответ. 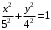 , , 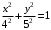 Задание 4. Найти уравнение плоскости, проходящей через точку М(1,1,1) перпендикулярно плоскостям, уравнения которых заданы: 2x-4y+z+2=0 и 4x-2y-z=0 Решение. Искомая плоскость перпендикулярна к двум заданным плоскостям и её нормальный вектор будет перпендикулярен к нормальным векторам, заданных плоскостей. Следовательно, нормальный вектор искомой плоскости будет коллинеарен векторному произведению нормальных векторов заданных плоскостей. Нормальные вектора заданных плоскостей : 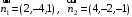 , ,Тогда 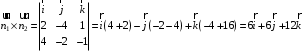 . .В качестве нормального вектора искомой плоскости возьмём вектор 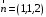 , уравнение плоскости, проходящей через точку М с нормальным вектором , уравнение плоскости, проходящей через точку М с нормальным вектором 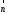 , запишется в виде , запишется в виде 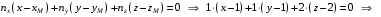 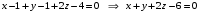 Ответ. 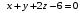 Задание 5. Найти уравнение прямой, проходящей через точку М(1,01) перпендикулярно прямым, уравнения которых заданы: x/1=y/2=z/2 и (x-1)/2=(y+1)/2=z/1 Решение. Искомая прямая перпендикулярна к двум заданным прямым и её направляющий вектор будет перпендикулярен к направляющим векторам заданных прямых. Следовательно, направляющий вектор искомой прямой будет коллинеарен векторному произведению направляющих векторов заданных прямых. Направляющие вектора заданных прямых : 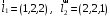 , ,Тогда  . .В качестве направляющего вектора искомой прямой возьмём вектор 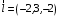 , уравнение прямой, проходящей через точку М с направляющим вектором , уравнение прямой, проходящей через точку М с направляющим вектором 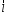 , запишется в виде , запишется в виде 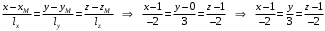 Ответ. 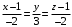 |
