психология задания 2-8. Занятие Решение задачи с помощью электронной таблицы Excel и системы компьютерной математики Mathcad
 Скачать 312.01 Kb. Скачать 312.01 Kb.
|
|
Практическое занятие № 2. Решение задачи с помощью электронной таблицы Excel и системы компьютерной математики Mathcad Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения y = 0,8551Ln(x) + 4,6586 переменной из нескольких уже известных значений. В состав M. Excel входит набор средств анализа данных (пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для анализа данных следует указать входные данные и выбрать параметры; анализ будет выполнен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде. Средства, включенные в пакет анализа данных, доступны через команду Анализ данных меню Сервис. Если этой команды нет в меню, необходимо загрузить надстройку Пакет анализа. Цель работы: проанализировать влияние функционально-технологических свойств рецептурных смесей на основе регрессионно-факторного анализа. Пример: В лабораторных условиях было исследовано влияние ферментного препарата глюкозооксидазы (х2) в сочетании с аскорбиновой кислотой (х1) на качество хлеба (табл.). Необходимо с помощью ЭВМ рассчитать, какой фактор (х1 или х2) оказывает большее влияние на пористость хлеба; построить эмпирическую линейную модель зависимости пористости хлеба y от фактора х1 или х2, оказывающего на него большее влияние; выявить, как изменится пористость хлеба, если величину глюкозооксидазы увеличить на 30% от среднего значения выборки. Таблица 2.1- Влияние ферментного препарата глюкозооксидазы в сочетании с аскорбиновой кислотой на качество хлеба
1. Создадим шаблон-таблицу в M. Excel. 2. Определим, какой фактор (количество аскорбиновой кислоты х1 или количество глюкозооксидазы х2) оказывает большее влияние на пористость хлеба с помощью коэффициента регрессии. Для этого построим матрицу коэффициентов корреляции: Сервис → Анализ данных → Корреляция (рис. 2.1). 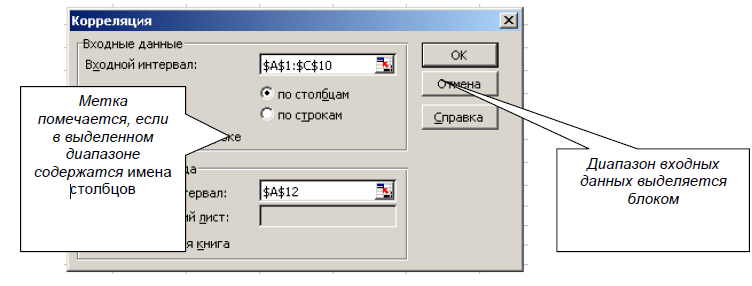 Рисунок 2.1 – Определение матрицы коэффициентов корреляции Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция). Коэффициент корреляции, как ковариационный анализ, характеризует область, в которой два измерения изменяются вместе. Коэффициент масштабируется таким образом, что его значение не зависит от единиц, в которых выражены переменные двух измерений. Таблица 2.2.- Матрица коэффициентов корреляции
Любое значение коэффициента корреляции должно находится в диапазоне от –1 до +1 включительно. Чем ближе по модулю коэффициент корреляции rхук 1, тем теснее связь между х и у. Если │rх1у│>│rх2у│, то фактор х1 оказывает большее влияние на у, чем х2. В результате имеем: rх1у = 0,304572452 – связь (между х1 и у) слабая; rх2у = -0,88317– связь (между х2 и у) умеренная обратная (т.е. с увеличением количества глюкооксидазы, пористость хлеба уменьшается). Значит │rх1у│<│rх2у│, поэтому фактор х1 оказывает меньшее влияние на у, чем х2. Следовательно, будем строить эмпирическую зависимость Метка помечается, если в выделенном диапазоне содержатся имена столбцов Диапазон входных данных выделяется блоком пористости хлеба у от количества глюкооксидазы х2. Построим эмпирическую модель зависимости пористости хлеба у от количества глюкооксидазы х2. Для этого используем встроенный пакет регрессионного анализа: Сервис → Анализ данных → Регрессия (рис. 2.2). 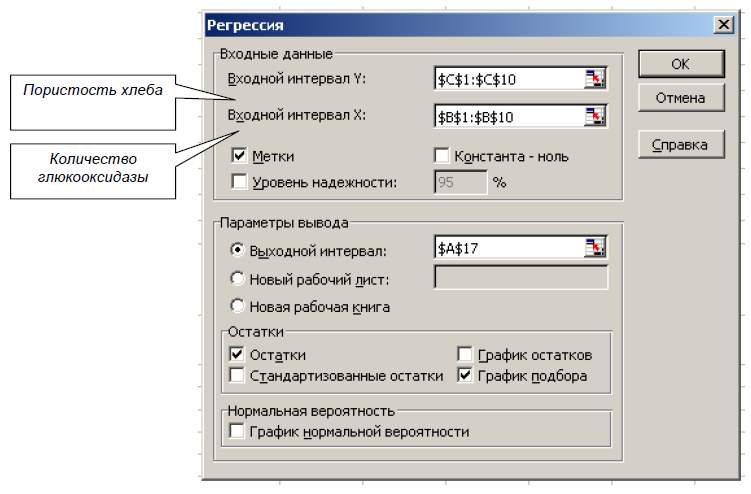 Рисунок 2.2 – Вид окна пакета «Регрессия» Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Получили зависимость: y=87,3– 29,1х2. Коэффициент детерминации R2=0,78, т.е. доля вариации у объясняется лишь на 78% вариацией (есть смысл «улучшить» модель для вычисления значения). Для добавления линии тренда к ряду данных следует: активизировать построенную на основе ряда данных диаграмму, т. е. щелкнуть в пределах области диаграммы. В главном меню появится пункт Диаграмма; после щелчка на этом пункте на экране появится меню, в котором следует выбрать команду Добавить линию тренда. Эти же действия легко реализуются, если навести указатель мыши на график, соответствующий одному из рядов данных, и щелкнуть правой кнопкой мыши; в появившемся контекстном меню выбрать команду Добавить линию тренда. На экране появится диалоговое окно Линия тренда с раскрытой вкладкой Тип (рис. 2.3). 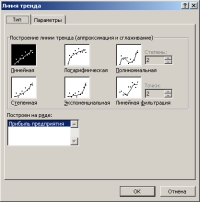 Рисунок 2.3 -Диалоговое окно Линия тренда с раскрытой вкладкой Тип После этого необходимо: Выбрать на вкладке Тип необходимый тип линии тренда (по умолчанию выбирается тип Линейный). Для типа Полиномиальная в поле Степень следует задать степень выбранного полинома. 1. В поле Построен на ряде перечислены все ряды данных рассматриваемой диаграммы. Для добавления линии тренда к конкретному ряду данных следует в поле Построен на ряде выбрать его имя. 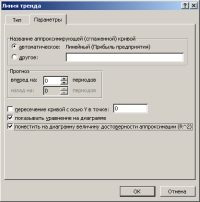 Рисунок 2.4 – Линия тренда При необходимости, перейдя на вкладку Параметры (рис. 2.4), можно для линии тренда задать следующие параметры: изменить название линии тренда в поле Название аппроксимирующей (сглаженной) кривой. задать количество периодов (вперед или назад) для прогноза в поле Прогноз; вывести в область диаграммы уравнение линии тренда, для чего следует включить флажок показать уравнение на диаграмме; вывести в область диаграммы значение достоверности аппроксимации R2, для чего следует включить флажок поместить на диаграмму величину достоверности аппроксимации (R^2); задать точку пересечения линии тренда с осью Y, для чего следует включить флажок пересечение кривой с осью Y в точке; щелкнуть на кнопке OK, чтобы закрыть диалоговое окно. Для того, чтобы начать редактирование уже построенной линии тренда, существует три способа: воспользоваться командой Выделенная линия тренда из меню Формат, предварительно выбрав линию тренда; выбрать команду Формат линии тренда из контекстного меню, которое вызывается щелчком правой кнопки мыши по линии тренда; двойным щелчком по линии тренда. На экране появится диалоговое окно Формат линии тренда (рис. 2.5), содержащее три вкладки: Вид, Тип, Параметры, причем содержимое последних двух полностью совпадает с аналогичными вкладками диалогового окна Линия тренда. На вкладке Вид, можно задать тип линии, ее цвет и толщину.  Рисунок 2.5 - Формат линии тренда Для удаления уже построенной линии тренда следует выбрать удаляемую линию тренда и нажать клавишу Delete. Достоинствами рассмотренного инструмента регрессионного анализа являются: относительная легкость построения на диаграммах линии тренда без создания для нее таблицы данных; достаточно широкий перечень типов предложенных линий трендов, причем в этот перечень входят наиболее часто используемые типы регрессии; возможность прогнозирования поведения исследуемого процесса на произвольное (в пределах здравого смысла) количество шагов вперед, а также назад; возможность получения уравнения линии тренда в аналитическом виде; возможность, при необходимости, получения оценки достоверности проведенной аппроксимации. К недостаткам можно отнести следующие моменты: построение линии тренда осуществляется лишь при наличии диаграммы, построенной на ряде данных; процесс формирования рядов данных для исследуемой характеристики на основе полученных для нее уравнений линий тренда несколько загроможден: искомые уравнения регрессий обновляются при каждом изменении значений исходного ряда данных, но только в пределах области диаграммы, в то время как ряд данных, сформированный на основе старого уравнения линии тренда, остается без изменения; в отчетах сводных диаграмм при изменении представления диаграммы или связанного отчета сводной таблицы имеющиеся линии тренда не сохраняются, то есть до проведения линий тренда или другого форматирования отчета сводных диаграмм следует убедиться, что макет отчета удовлетворяет необходимым требованиям. Линиями тренда можно дополнить ряды данных, представленные на диаграммах типа график, гистограмма, плоские ненормированные диаграммы с областями, линейчатые, точечные, пузырьковые и биржевые. Нельзя дополнить линиями тренда ряды данных на объемных, нормированных, лепестковых, круговых и кольцевых диаграммах. Пример: Регрессионно-факторный анализ технологических моделей. Цели работы: проанализировать влияние функционально-технологических свойств рецептурных смесей на основе регрессионно-факторного анализа. Таблица 1 - Влияние ферментного препарата глюкозооксидазы в сочетании с аксорбиновой кислотой на качество хлеба
Таблица 2 - Матрица коэффициентов корреляции
Вывод: количество глюкозооксидазы оказывает большое влияние на пористость хлеба, поскольку значение его коэффициента корреляции по модулю близко к единице. Эмпирическая модель зависимости пористости хлеба y от количества аскорбиновой кислоты x1 ВЫВОД ИТОГОВ
Дисперсионный анализ
ВЫВОД ОСТАТКА
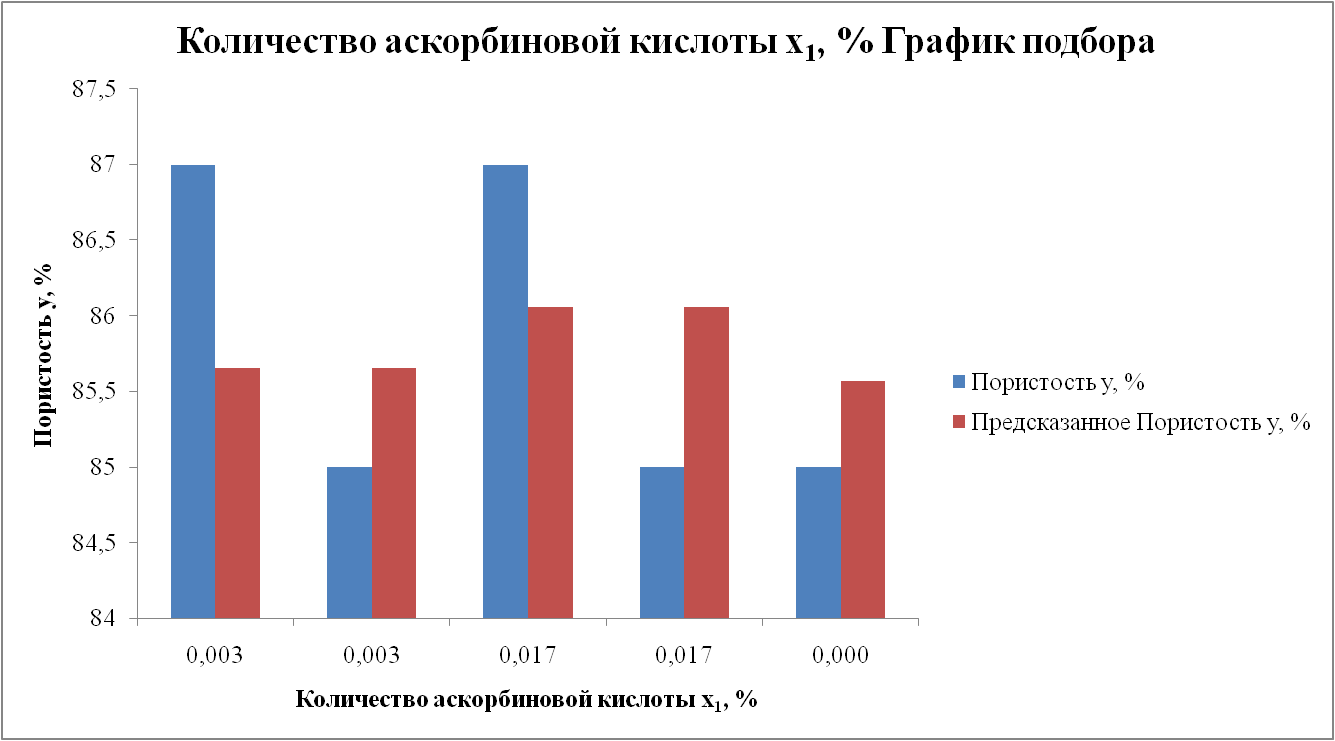 Эмпирическая модель зависимости пористости хлеба y от количества глюкозооксидазы x2 ВЫВОД ИТОГОВ
Дисперсионный анализ
ВЫВОД ОСТАТКА
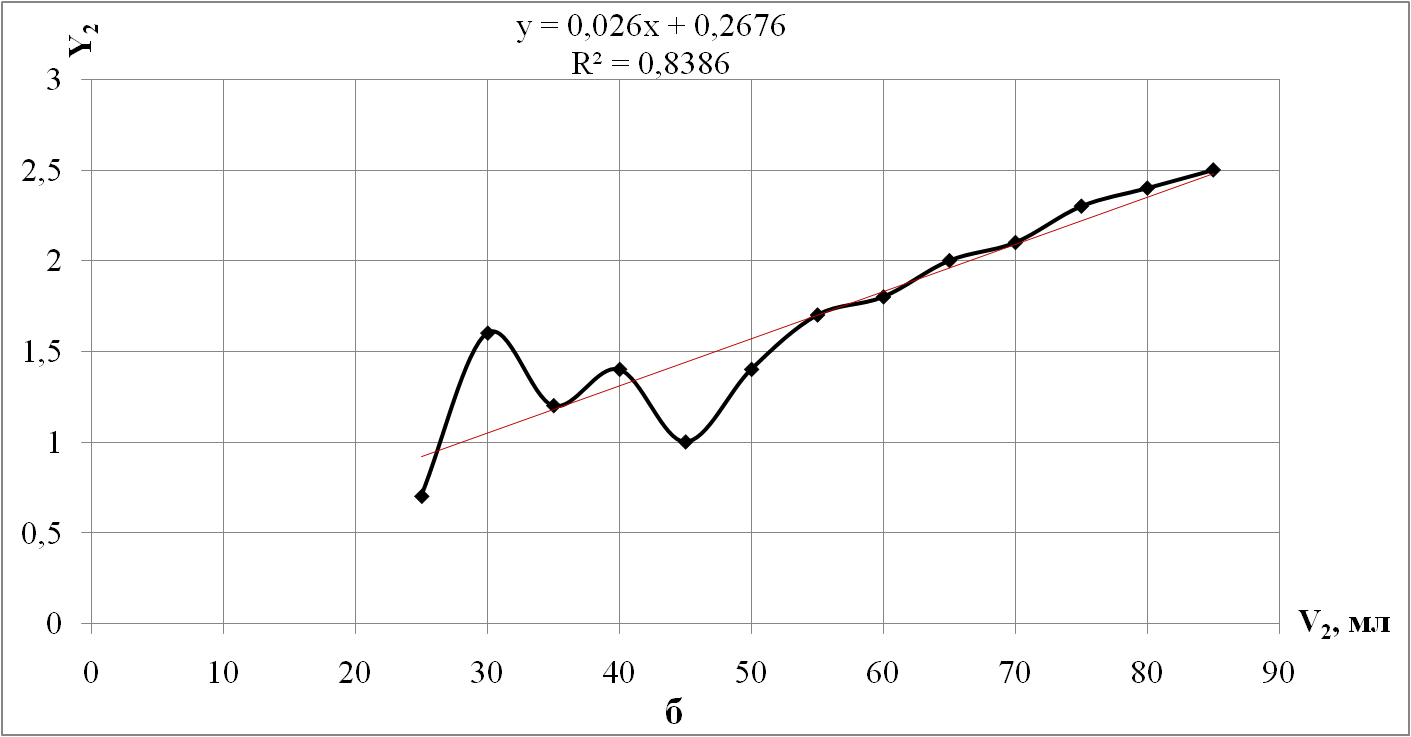 Задание: Определить, какой фактор (количество аскорбиновой кислоты х1 или количество глюкозооксидазы х2) оказывает большее влияние на пористость хлеба с помощью коэффициента регрессии. В качестве исходных данных брать таблицу 2.1. Отчет о проделанной работе должен содержать: Название практического занятия _______________________________________________________________________________________________________________________________ Цель и задачи _______________________________________________________________________________________________________________________________ Алгоритм работы _______________________________________________________________________________________________________________________________ Исходные данные _______________________________________________________________________________________________________________________________ Расчет, графики _______________________________________________________________________________________________________________________________ Результаты расчета и выводы по работе _______________________________________________________________________________________________________________________________ Ответы на контрольные вопросы ____________________________________________________________________________________________________________________________________ Контрольные вопросы Дайте понятие статической модели? Дайте понятие динамической модели? Приведите пример модели с распределенными параметрами. Приведите пример модели с сосредоточенными параметрами. При решении, каких задач используются динамические и статические модели? Какие виды экспериментов вы знаете? В чем преимущество активного эксперимента? Какие переменные называются факторами? Что такое факторное пространство? Дайте понятие поверхности отклика? В виде, какого уравнения чаще представляются уравнения регрессии? Какие методы расчета коэффициентов уравнения регрессии вы знаете? Поясните сущность метода наименьших квадратов? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
