Семинар. ПЗ1. Занятие 1 примеры заданий с решениями i. Алгебра высказываний

• Название: Занятие 1 примеры заданий с решениями i. Алгебра высказываний
• Анкор: Семинар
• Дата: 02.05.2023
• Размер: 40.93 Kb.
• Имя файла: ПЗ1.docx
• Тип: Занятие; #1102307

^{Практическое занятие №1}

ПРИМЕРЫ ЗАДАНИЙ С РЕШЕНИЯМИ
I.Алгебра высказываний
1. Определить, какие предложения являются высказываниями:

а) Ты пойдешь завтра на занятия?

б) Сегодня идёт снег.

в) Число 7 является чётным.

г) Числа 7 и 77.

Решение:

1) Выясним, является ли данная запись предложением.

В задании запись под буквой г) не является предложением, поэтому его не рассматриваем.

2) Выясним, является ли данное предложение — утверждением (повествовательным предложением).

В задании запись под буквой а) не является утверждением (это вопросительное предложение), поэтому его не рассматриваем.

3) Выясним, можно ли однозначно сказать каким является утверждение — истинным либо ложным.

В задании запись под буквой б) не позволяет однозначно определить логическое значение, поэтому его не рассматриваем.

В задании запись под буквой в) позволяет однозначно определить логическое значение. Это высказывание, которое является ложным.
2. Запишите формулу для данного высказывания: «Если я сдам экзамен по математике и физике, то получу подарок от родителей и буду получать стипендию».

Решение:

1) Выделим различные простые высказывания и обозначим их различными буквами:

А: Я сдам экзамен по математике.

В: Я сдам экзамен по физике.

С: Получу подарок от родителей.

D: Буду получать стипендию.

2) Определить логические операции, встречающиеся в высказывании: импликация и конъюнкция.

3) Обозначить их соответствующими символами: , .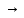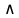

4)Записать последовательно буквы и символы, расставляя скобки по смыслу: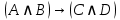
3. Определить логическое значение сложного высказывания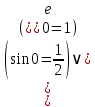

.

Решение:

1)  Определим простые высказывания, их логические значения:

A: ;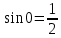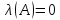

B: ;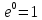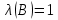

C: ;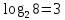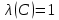

D: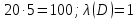
2)  Определим логические операции, их значения:

Дизъюнкция: .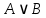

Логическое значение: .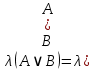

Конъюнкция: .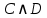

Логическое значение: .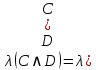

Импликация: .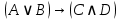

Логическое значение: .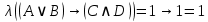

Вывод: Логическое значение высказывания равно 1, то есть высказывание является истинным.
4. Построить таблицу истинности для формулы алгебры высказываний: 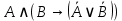. Определить вид формулы.

Решение:

1)Определим количество различных букв в формуле: в формуле две различных буквы А и В, то есть два высказывания.

2) Определим количество строчек в таблице истинности по формуле 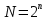(где N — число строк, n — число высказываний): в таблице истинности 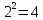строчки.

3) Определим последовательность операций: отрицание А, отрицание В, дизъюнкция, импликация, конъюнкция.

4) Строим таблицу истинности (столбцы и комбинации 1, 0) и заполняем таблицу истинности (логические значения операций, результирующий столбец):

1	2	3	4	5	6	7 (результирующий столбец)
1	1	0	0	Используем значения 3 и 4 столбцов	Используем значения 2 и 5 столбцов	Используем значения 1 и 6 столбцов
1	0	0	1	1	1	1
0	1	1	0	1	1	0
0	0	1	1	1	1	0

Вывод: Так как результирующий столбец содержит 1 и 0, то формула выполнимая.
5. Определите, являются ли формулы равносильным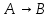и и .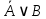

Решение:

1)Строим одну таблицу истинности для формул:

1	1	0	1	1
1	0	0	0	0
0	1	1	1	1
0	0	1	1	1

2) Сравниваем результирующие столбцы (последние столбцы в таблицах).
Вывод: Количество и последовательность 1 и 0 результирующих столбцов совпадает, следовательно, формулы равносильные.

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ НА ЗАНЯТИИ
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
1.1. Используя определение, укажите, какие из предложений являются высказываниями. Определите логическое значение высказывания.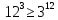

1. 
   
   
2. 
   Мариус Петипа — российский и французский балетмейстер.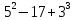
   
3. 
   
   
4. 
   Через две точки на плоскости можно провести более одной прямой.
   
5. 
   Длина отрезка 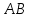равна длине отрезка .
   
6. 
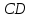   На улице сегодня солнечно?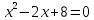
   
7. 
   
   

1.2. Используя определение, укажите отрицание, конъюнкцию, дизъюнкцию, импликацию, эквиваленцию высказываний. Определите их логическое значение. Запишите высказывания с помощью формул.

а) Если 12 делится на 4, то 12 делится на 2.

б) 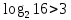 тогда и только тогда, когда .

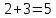в) Неверно, что 100 больше 7.

г) 15 делится на 5 и на 2.

д) Квадратное уравнение имеет один или два действительных корня.

е) Логарифмическая функция чётна и непрерывна.

ж) Если прямые на плоскости имеют более одной точки пересечения, то они совпадают.

з) Неверно, что 123 делится на 11.
1.3. Определите логическое значение сложных высказываний: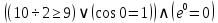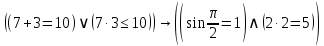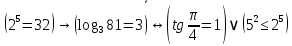

1. 
   ;
   
2. 
   ;
   
3. 
   ;
   

г) ;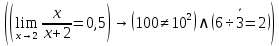

д) .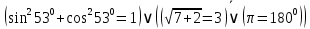
1.4. Найдите истинностное значение высказывания С, если известно истинностное значение сложного высказывания: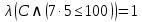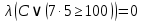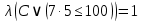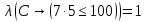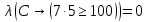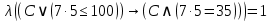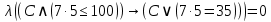

1. 
   ;
   
2. 
   ;
   
3. 
   ;
   
4. 
   ;
   
5. 
   ;
   
6. 
   ;
   
7. 
   .
   

1.5. Определите, является ли последовательность символов формулой. Если не является — объясните почему. Для каждой формулы выпишите всевозможные подформулы.

а) б)	в) г)
д)

1.6. Постройте таблицу истинности для следующих формул алгебры высказываний. Определите вид формулы.

а)  ; б)  ; в)  ;

г) ; д) .

1.7. Укажите формулы, равносильные данной :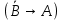

а)  ;	б)  ;
в)  ;	г)  .

1.8. Решите задачу. На вопрос: «Кто из трех студентов сдал экзамен?» получен верный ответ — «Если сдал первый, то сдал и третий, но не верно, что если сдал второй, то сдал и третий». Кто сдал экзамен?

ДОМАШНЕЕ ЗАДАНИЕ № 1
№ 1. Следующее сложное высказывание разбейте на простые и запишите составное высказывание, используя знаки логических связок.

1. 
   Не верно, что, если сегодня пятница, то завтра будет понедельник или вторник.
   
2. 
   Если 25 делится на 5, то 5 не делится на 25, и если 10 не делится на 2, то 2 не делится на 10.
   
3. 
   Две прямые пересекаются тогда и только тогда, когда 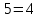, показательная функция возрастает и не пересекает ось ординат.
   
4. 
   11 простое число или если 100 делится на 10, то 100 делится и на 5.
   

№ 2. Высказывание P означает «сегодня идет дождь», Q — «сегодня ясно», R — «сегодня идет снег», S — «вчера было пасмурно». Расшифруйте и запишите следующие высказывания:

а) ;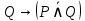

б) ;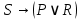

в) ;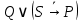

г) .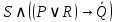
№ 3. Постройте таблицу истинности следующих высказываний. Определите вид формулы.

а)  ;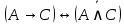

б)  .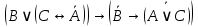
№ 4. Сформулируйте отрицания следующих предложений в утвердительной форме, т.е. так, чтобы они не начинались со слов «неверно, что».

а) Число 10 делится на 5 и на 2.

б) Две прямые на плоскости параллельны или пересекаются.

в) Если треугольник равнобедренный, то он прямоугольный.

г) Если число делится на 6, то оно делится на 2 и на 3
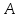
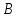
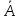
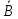
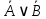
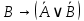
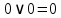
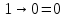
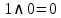
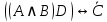
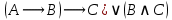
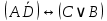
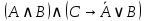
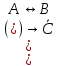
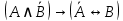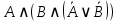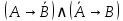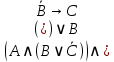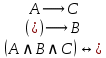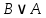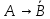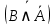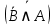