Практическая работа №2 по математике. Практическое задание №2. Занятие 2 Десятичные дроби
 Скачать 118.19 Kb.
|
|
Практическое занятие 2 Десятичные дроби 1. Чтобы обратить десятичную дробь в обыкновенную дробь, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе единице с нулями, причем нулей должно быть столько, сколько цифр справа запятой. Например,  2. Чтобы обратить обыкновенную дробь в десятичную, достаточно разделить числитель на знаменатель по правилу деления десятичной дроби на целое число. Например,  Заметим что при этом может получиться бесконечная десятичная дробь. Например,  3. Бесконечная десятичная дробь, в которой начиная с некоторого разряда, цифры повторяются, называется периодической. Например, 0,333..., 0,6777...; Любую обыкновенную дробь можно записать в виде конечной десятичной дроби, либо бесконечной периодической дроби. Повторяющаяся группа цифр (заключенная в скобках) называется периодом дроби. Можно было бы вместо 0,(27) написать 0,2(72), но эта запись была бы длиннее. Теорема. Если в разложение знаменателя несократимой дроби на простые множители не входят цифры 2 и 5, то при обращении этой дроби в бесконечную десятичную, получится чистая периодическая дробь, т.е. период начинается разу после запятой. Если же в разложение знаменателя входят цифры 2 или 5, то периодическая дробь будет смешанной (между запятой и периодом будет столько цифр, сколько единиц в наибольшем показателе числа 2 или 5). Например, 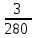 – это несократимая дробь. Разложим знаменатель на простые множители.  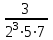, видим в знаменателе и 2, и 5. Значит, наша дробь представима в виде бесконечной периодической дроби, причем дробь будет смешанной, и цифр перед первым периодом будет 3 (так как видим 23).Теорема. Каждую бесконечную периодическую десятичную дробь (чистую или смешанную) можно записать в виде дроби 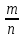 .Рассмотрим на конкретных примерах. Пусть дана периодическая десятичная дробь 0,(24), то есть 0,242424…24… Обозначим соответствующее ей число через а. а = 0, 2424…24… Если перенести запятую на две цифры право, число а увеличится в 100 раз, и мы получим 100а = 24,2424…24… 100а = 24+0,2424…24… 100а = 24+а 99а = 24 а = 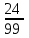 = 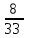Точно также обращается в обыкновенную дробь любая чистая периодическая десятичная дробь. Аналогично выводится правило для обращения в обыкновенную дробь смешанной периодической десятичной дроби. Переведем 0,5(21) в обыкновенную Пусть 0,5(21) = х. 0,5(21)=0,52121…21…= х Умножим обе части на 10 5,2121…21.. = 10х 10х = 5+0,2121…21… По предыдущему правилу 0,2121…21… = 0,(21) = 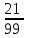 10х = 5+ 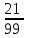10х = 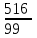 х = 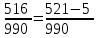 Правило перевода бесконечной периодической дроби в обыкновенную таково: Чтобы обратить чистую периодическую десятичную дробь в обыкновенную, надо из числа стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после десятоок дописать столько нулей,сколько цифр между запятой и первым периодом. Например,  Упражнения с решениями. Обратить периодическую дробь в обыкновенную: а) 0,(3); б) 0,2(1); в) 0,2(19); г) 3,(73) д) 2,2(41) Решение: а) Числитель искомой дроби равен периоду данной дроби, т.е. 3, а знаменатель содержит цифру 9 столько раз, сколько цифр в периоде, т.е. один раз. Итак,  б) Числитель дроби есть разность между числом, стоящим после запятой (включая период 1), и числом, стоящим до периода (после запятой). Знаменатель содержит цифру 9 один раз (так как после одна цифра) и один нуль (столько цифр между запятой и периодом). Итак,  в)  г)  д)  Задания для самостоятельного решения.  |