Лаб работа. ЛАБОРАТОРНОЕ ЗАНЯТИЕ 6. Занятие 6 Резервирование замещением в режиме облегченного (теплого) резерва и в режиме ненагруженного (холодного) резерва

• Название: Занятие 6 Резервирование замещением в режиме облегченного (теплого) резерва и в режиме ненагруженного (холодного) резерва
• Анкор: Лаб работа
• Дата: 28.10.2021
• Размер: 131 Kb.
• Имя файла: ЛАБОРАТОРНОЕ ЗАНЯТИЕ 6.doc
• Тип: Занятие; #257965

ЛАБОРАТОРНОЕ ЗАНЯТИЕ №6

Резервирование замещением в режиме облегченного (теплого) резерва и в режиме ненагруженного (холодного) резерва.

Теоретические сведения.

В этом случае резервные элементы находятся в облегченном режиме до момента их включения в работу. Надежность резервного элемента в этом случав выше надежности основного элемента, так как резервные элементы находятся в режиме недогрузки до момента их включения в работу.

Вероятность отказа резервированной системы с облегченным резервированием определяется соотношением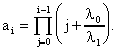

(5.1)

где

(5.2)

Здесь ₁ - интенсивность отказа резервного элемента в режиме недогрузки до момента включения его в работу ; ₀ - интенсивность отказа резервного элемента в состоянии работы; m - кратность резервирования или количество резервных элементов. Вероятность безотказной работы системы с облегченным резервированием определяется формулой

(5.3)

Определим среднее время безотказной работы системы с облегченным резервированием. Имеем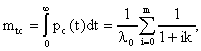

(5.4)

где

(5.5)

Определим частоту отказов f_c(t) системы с облегченным резервированием.

Имеем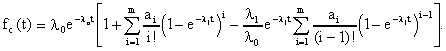

(5.6).

Определим интенсивность отказов _с(t) системы с облегченным резервированием.

Получим

(5.7)

При ₁ =0 имеем режим ненагруженного (холодного) резерва. Вероятность отказа резервированной системы с ненагруженным резервированием определяется соотношением

(5.8)

Вероятность безотказной работы системы с ненагруженным резервом определяется формулой

(5.9)

Определим среднее время безотказной работы системы с ненагруженным резервом. Имеем

(5.10)

Определим частоту отказов f_c(t) системы с ненагруженным резервом.

Имеем

(5.11)

Определим интенсивность отказов _с(t) системы с ненагруженным резервом.

Получим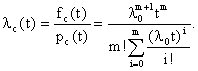

(5. 12)

Решение типовых задач.

Задача 1. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента m_t = 1000 час. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти вероятность безотказной работы системы Р_с(t), среднее время безотказной работы системы m_tс, а также частоту отказов f_c(t) и интенсивность отказов _с (t)

в момент времени t = 50 час в следующих случаях:

а) нерезервированной системы,

б) дублированной системы при включении резерва по способу замещения (ненагруженный резерв).

Решение:

а)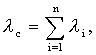

где _с - интенсивность отказов системы, _i - интенсивность отказов i - го элемента; n = 10,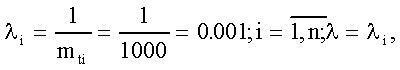



ед/час ,

p_c(t)= ;

f_c(t)=_c(t)p_c(t) ;

f_c(50)=_{c =0.01e}^-0.0150610-3 1/час ; _c(50)=0.01 ед/час .

б) m_tc= ; m=1 ;

m_tc= =200 час .

Определяем Р_c(t) по формуле



Так как ₀=_с , то

P_c(t)=e^-сt(1+_ct) .

Определяем f_c(t). Имеем

Определяем _c (t) . Получим _c(t)=

0пределяем P_c(50), f_c(50), _c(50).Имеем

p_c(50)=e^-0.0150(1+0.0150)=e^-0.51.5=0.91

f_c(50)=0.01^{2 *}50e^(-0.01*50) =310 ^-3ед/час ,

_c(50)= ед/час .

Задача 2. Радиопередатчик имеет интенсивность отказов ₀=0,4*10^-3 ед/час. Его дублирует такой же передатчик, находящийся до отказа основного передатчика в режиме ожидания (в режиме облегченного резерва). В этом режиме интенсивность отказов передатчика ₁= 0,06*10^-3 ед/час. Требуется вычислить вероятность безотказной работы передающей системы в течение времени t = 100 час., а также среднее время безотказной работы m_tс, частоту отказов f_c(t) и интенсивность отказов _с(t).

Решение. В рассматриваемом случае кратность резервирования m = 1. Используя формулу (5.З), получим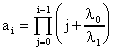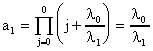

;

; .

Тогда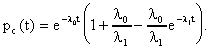

(5.13)

Из (5.13) имеем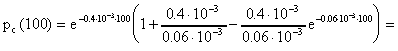



0.96[1+6.67-6.67(1-0.006)]0.998 .

Определим m_tс по формуле (5.4.). Получим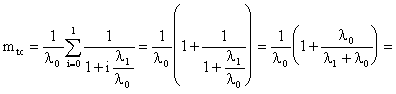



= 4668 час .

Определим f_c(t) . Имеем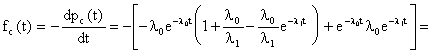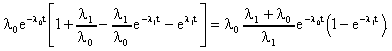



=

Перепишем (5.13) в виде



Определим _с(t). Получим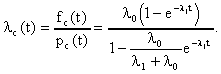



Задача 3. Вероятность безотказной работы преобразователя постоянного тока в переменный в течении времени t=1000 час. равна 0,95, т. е. Р(1000) = 0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включается в работу при отказе первого (режим ненагруженного резерва). Требуется рассчитать вероятность безотказной работы и среднее время безотказной работы системы, состоящей из двух преобразователей, а также определить частоту отказов f_c(t) и интенсивность отказов _с(t) системы.

Решение. В рассматриваемом случае кратность резервирования m = 1. Используя формулу (5.9), получим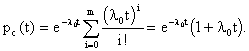

(5.14)

Так как для отдельного преобразователя имеет место экспоненциальный закон надежности, то

, (5.15)

где Р(t)- вероятность безотказной работы преобразователя; ₀ - интенсивность отказов преобразователя в состоянии работы.

Из (5.15) имеем

P(1000)=e^-o*1000 =0,95 .

Из приложения П.7.14 [1] получим ₀*1000=0,051,

откуда ₀=0,051/10000,5*10^-4 ед/час.

Тогда из (5.14) имеем

P_c(1000)=0,95(1+0,05)=0,9975 .

Определим m_tc по формуле (5.10). Получим

m_tc = (m+1)/₀=2/₀=2/(0,5*10^-4) = 40000 час .

Отметим, что среднее время безотказной работы нерезервированного преобразователя равно

m_tc =1/₀=20000 час.

Определим частоту отказов f_c(t) по формуле (5.11). Имеем



Определим _с(t). Получим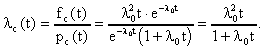



Задачи для самостоятельного решения.

Задача 4. Система состоит из двух одинаковых элементов. Для повышения ее надежности конструктор предложил дублирование системы по способу замещения с ненагруженным состоянием резерва. Интенсивность отказов элемента равна 0,510^-3 ед/час. Требуется определить вероятность безотказной работы системы P_c(t), среднее время безотказной работы m_tc , частоту отказов f_c(t) , интенсивность отказов _с(t).

Задача 5. Схема расчета надежности изделия приведена на рис.5.2. Необходимо определить вероятность безотказной работы P_c(t), частоту отказов f_c(t), интенсивность отказов _с(t) изделия. Найти _с(t) при t = 0.

Задача 6. Передающее устройство состоит из одного работающего передатчика (интенсивность отказов =8*10^-3 1/час) и одного передатчика в облегченном резерве (₀ = 8*10^-4 1/час) . Требуется определить вероятность безотказной работы устройства P_c(t) , среднее время безотказной работы устройства m_tc. Определить Pc(t) при t = 20 час.

Задача 7. В радиопередающем канале связной системы используется основной передатчик П₁, два передатчика П₂ и П₃, находящиеся в ненагруженном резерве. Интенсивность отказов основного работающего передатчика равна ₀=10^-3 1/час. С момента отказа передатчика П₁ в работу включается П₂, после отказа передатчика П₂ включается П₃. При включении резервного передатчика в работу его интенсивность отказов становится равной ₀. Считая переключатель абсолютно надежным, определить вероятность безотказной работы

P_c(t) радиопередающего канала, среднее время безотказной работы m_tc канала. Определить также P_c(t) при t=100 час.

Задача 8. Устройство автоматического поиска неисправностей состоит из двух логических блоков. Среднее время безотказной работы этих блоков одинаково и для каждого из них равно m_t= 200 час. Требуется определить среднее время безотказной работы устройства m_tc для двух случаев: а) имеется ненагруженный резерв всего устройства; б) имеется ненагруженный резерв каждого блока.