Главная страница
Навигация по странице:

  • Пример

  • Задача

    		•

    Практическое задание. Занятие Методы составления первоначального плана поставок


    Скачать 0.81 Mb.
    НазваниеЗанятие Методы составления первоначального плана поставок
    Дата04.04.2023
    Размер0.81 Mb.
    Формат файлаdocx
    Имя файлаПрактическое задание.docx
    ТипЗанятие
    #1037593
    страница3 из 4
    1   2   3   4

    Особый случай построения первоначального плана поставок


    Выше мы отмечали, что при построении первоначального плана поставок должно соблюдаться следующее правило: число отмеченных клеток в таблице поставок равняется сумме чисел строк и столбцов минус единица.

    Однако иногда это правило нарушается. Рассмотрим пример для которого это правило не соблюдается. Это, так называемый, особый случай.

    Пример 3. У поставщиков 𝐴!, 𝐴!, 𝐴! сосредоточено соответственно 80, 30, 40

    единиц некоторого однородного груза. Этот груз необходимо доставить

    потребителям 𝐵!, 𝐵!, 𝐵! в количестве 60, 20 и 70 единиц соответственно.

    Стоимость перевозок единицы груза от поставщиков к потребителям задается

    матрицей коэффициентов затрат
    1
    3
    5



    𝐶 =
    3
    3
    2
    .




    4
    1
    2




    Необходимо построить первоначальный план поставок методом северо- западного угла и вычислить их суммарную стоимость.

    Решение.
    Рассмотрим алгоритм решения.

    Шаг 1. Для клетки (1,1): 𝑥!! = min 𝑀!, 𝑁! = min 80, 60 = 60. Исключаем из решения первый столбец.

    60

    20

    70

    80
    1

    60
    3
    5


    30
    3
    3
    2


    40
    4
    1
    2

    Шаг 2. Для клетки (1,2): 𝑥!" = min 𝑀!, 𝑁! = min 80 − 60, 20 = 20.

    Исключаем из решения второй столбец и первую строку одновременно. Это

    приведет к нарушению правила о котором говорилось в начале параграфа 3.

    60

    20

    70

    80
    1

    60
    3

    20
    5


    30
    3
    3
    2


    40
    4
    1
    2

    Поэтому в первой строке или во втором столбце одну пустую клетку надо перевести в отмеченные с нулевым объемом поставок. Пусть это будет клетка (2,2). Так поступают всякий раз, когда на одном шаге приходится исключать одновременно и строку, и столбец.

    60

    20

    70

    80
    1

    60
    3

    20
    5


    30
    3
    3

    0
    2


    40
    4
    1
    2

    Далее решение задачи производится по обычной схеме. Окончательно получаем следующую таблицу поставок

    60

    20

    70

    80
    1

    60
    3

    20
    5


    30
    3
    3



    2









    0






    30


    40
    4
    1
    2




    40



    Суммарную стоимость всех поставок вычислим по формуле

    nm

    Fcijxij160 320 30 2 30 2 40 260.

    j1 i1

    Задача 3. У поставщиков 𝐴!, 𝐴!, 𝐴! сосредоточено соответственно 80, 30, 50

    единиц некоторого однородного груза. Этот груз необходимо доставить

    потребителям 𝐵!, 𝐵!, 𝐵! в количестве 20, 60 и 80 единиц соответственно.

    Стоимость перевозок единицы груза от поставщиков к потребителям задается

    матрицей коэффициентов затрат
    1
    3
    4



    𝐶 =
    3
    1
    2
    .




    4
    1
    2




    Необходимо построить первоначальный план поставок методом северо- западного угла и вычислить их суммарную стоимость.

    Практическое занятие 3.

    Системы массового обслуживания

    1. Процесс гибели и размножения

    В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов − процесс гибели и размножения. Название этого процесса связано с биологией, где этот процесс представляет собой математическую модель численности особей в популяции. Размеченный граф состояний этого процесса представлен на рис. 1.



    Рис. 1. Размеченный граф состояний процесса гибели и размножения

    Рассматривается многоканальная СМО, которая содержит n каналов и пребывает в состояниях:

    𝑆! – все каналы свободны;

    𝑆! – один канал занят;

    𝑆! – два канала заняты и т.д.

    Переход из одного состояния в другое происходит с соответствующими интенсивностями, как указано для n возможных состояний системы на размеченном графе (рис. 1).

    Переходы в рассматриваемой системе могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния 𝑆! возможны переходы только в состояние 𝑆!!! или в состояние 𝑆!!! .

    Предполагается, что все потоки событий, переводящие систему по стрелкам графа, являются простейшими.

    Составим и решим систему алгебраических уравнений для предельных вероятностей.

    Согласно правилу составления таких уравнений имеем: для состояния 𝑆! : 𝑝!𝜆!" =𝑝!𝜆!";

    для состояния 𝑆! : 𝑝!𝜆!"+𝑝!𝜆!" =𝑝!(𝜆!"+𝜆!").

    После раскрытия скобок во втором выражении и учете первого равенства слагаемые 𝑝!𝜆!" и 𝑝!𝜆!" взаимно уничтожаются. После этого уравнение для состояния 𝑆! принимает следующий вид:

    𝑝!𝜆!" =𝑝!𝜆!".

    Записывая аналогичные уравнения для предельных состояний других состояний, можно получить следующую систему алгебраических уравнений:

    𝑝!𝜆!" =𝑝!𝜆!";

    𝑝!𝜆!" =𝑝!𝜆!";

    ⋯

    𝑝!!!𝜆!!!,! =𝑝!𝜆!,!!!;

    ⋯

    𝑝!!!𝜆!!!,! =𝑝!𝜆!,!!!,

    к которой добавляется условие нормировки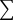

    !

    𝑝! =1.

    !!!

    Решеная полученную систему уравнений, можно получить

    𝜆!" 𝜆!"𝜆!" 𝜆!!!,! ⋯ 𝜆!"𝜆!" !!

    𝑝! =1+𝜆!"+𝜆!"𝜆!"+𝜆!,!!! ⋯ 𝜆!"𝜆!" ;

    𝜆 𝜆 𝜆 𝜆 𝜆 𝜆

    𝑝! 𝜆!" 𝜆!"𝜆!" 𝜆!,!!! ⋯ 𝜆!"𝜆!" . (1)
    1   2   3   4

    написать администратору сайта