Практическое задание. Занятие Методы составления первоначального плана поставок

• Название: Занятие Методы составления первоначального плана поставок
• Дата: 04.04.2023
• Размер: 0.81 Mb.
• Имя файла: Практическое задание.docx
• Тип: Занятие; #1037593
• страница: 4 из 4

Пример 1. Найти предельные вероятности для процесса гибели и размножения, размеченный граф состояний которого имеет следующий вид (на графе указаны интенсивности потоков)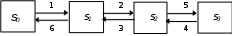



Решение. Для решения примера воспользуемся формулами (1):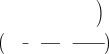

!!

^{𝑝! = 1+}𝜆_𝜆!!""_+𝜆𝜆!!""𝜆𝜆!!""⁺_𝜆𝜆!!,"!𝜆𝜆!!""𝜆𝜆!!""

1 2 ∙ 1 5 ∙ 2 ∙ 1 ^!! 36

= 1+ + + ==0,706;

6 3 ∙ 6 4 ∙ 3 ∙ 6 51

𝑝! 𝜆!" 6 ;

𝑝! 𝜆!"𝜆!" 3 ∙ 6 ;

𝑝! =𝜆𝜆!!,"!𝜆𝜆!!""𝜆𝜆!!""𝑝! =54 ∙∙ 23 ∙∙ 61𝑝! =0,098.

Одноканальная СМО с отказами

Пусть СМО имеет один канал обслуживания, на вход которой поступает простейший поток заявок с интенсивностью λ. Заявки обслуживаются с некоторой интенсивностью µ. Образование очереди не допускается. Если заявка застала обслуживающий канал занятым, то она покидает систему обслуживания.

Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром µ.

Среднее время обслуживания одной заявки 𝑡_обсл =¹𝜇.

Необходимо определить предельные вероятности состояний СМО и показатели ее эффективности. СМО имеет два состояния: 𝑆_! – канал свободен;

𝑆_! – канал занят.

Размеченный граф состояний одноканальной СМО с отказами представлен на рисунке.

	λ
S0		S1

μ

Систему уравнений для предельных состояний СМО в этом случае можно записать следующим образом

𝑝𝑝_!!𝜆𝜇==𝑝𝑝_!!𝜇𝜆;.

Поскольку уравнения совпадают, то имеем одно уравнение к которому добавляется условие нормировки

𝑝_!+𝑝_! =1.

Тогда предельные вероятности равны

𝜇 𝜆

𝑝_! =𝜆+𝜇 ; 𝑝_! =𝜆+𝜇.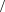

Отметим, что время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром µ. Поэтому среднее время обслуживания одной заявки 𝑡_обсл =¹𝜇.

Определим показатели эффективности работы одноканальной СМО с отказами:

1. 
   вероятность отказа 𝑝_отк (вероятность того, что заявка покинет систему необслуженной) равна предельной вероятности состояния 𝑆_!
   

𝜆

𝑝_отк =𝑝_! =𝜆+𝜇 ;

2. 
   относительная пропускная способность Q (вероятность того, что заявка будет обслужена) равна предельной вероятности состояния 𝑆_!
   

𝜇

𝑄=𝑝_! =𝜆+𝜇 ;

3. 
   абсолютная пропускная способность A (среднее числу заявок, которое СМО может обслужить в единицу времени) равна произведению Q на интенсивность потока заявок λ
   

𝜇 ∙ 𝜆

𝐴=𝑄 ∙ 𝜆=.

𝜆+𝜇

Пример 2. Имеется одноканальная телефонная линия. Заявка-вызов поступившая в момент, когда линия занята, получает отказ. Простейший поток заявок поступает с интенсивностью λ = 50 звонков в час. Средняя продолжительность разговора три минуты. Определить показатели эффективности работы СМО.

Решение. Поскольку средняя продолжительность разговора три минуты (3/60 = 0,05 часа), то интенсивность обслуживания заявки будет равна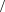

𝜇=1 𝑡обсл =1 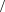0,05=20звоков час .

Определим показатели эффективности работы СМО:

1. 
   вероятность отказа 𝑝_отк
   

𝜆 50

𝑝_отк =𝜆+𝜇=50+20=0,714;

2. 
   относительная пропускная способность Q
   

𝜇 20

𝑄= = =0,286;

𝜆+𝜇 70

3. 
   абсолютная пропускная способность A
   

𝜇 ∙ 𝜆 20 ∙ 50

𝐴=𝑄 ∙ 𝜆= = =14,3 (звонка/час). 𝜆+𝜇 70

Многоканальная СМО с отказами

Рассмотрим теперь многоканальную СМО с отказами. Пусть СМО содержит n обслуживающих каналов на которые поступает поток заявок с интенсивностью λ.

Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром µ.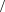

Среднее время обслуживания одной заявки 𝑡_обсл =¹𝜇.

Этот поток обслуживается одним каналом с интенсивностью µ, двумя каналами с интенсивностью 2µ, тремя − 3µ и т.д.

Обозначим состояния СМО 𝑆_! , 𝑆_! , ⋯ , 𝑆_! , ⋯ , 𝑆_! , где 𝑆_! – состояние СМО, когда в ней находятся k заявок, т.е. k каналов заняты обслуживанием. Граф состояний СМО в этом случае (он соответствует процессу гибели и размножения) можно представить в виде



Введем понятие приведенной интенсивности потока ρ, которая определяется соотношением

𝜆

𝜌=.

𝜇

Величина ρ представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

Тогда по аналогии с формулами (1) нетрудно получить формулы для вычисления предельных вероятностей состояний многоканальной

СМО с отказами (формулы Эрланга)

𝑝_! =(1+𝜌+𝜌2!! +𝜌3!! +⋯+𝜌𝑛!! _!!; )

𝜌! 𝜌!

𝑝_! =𝜌 ∙ 𝑝_!; 𝑝_! =2! 𝑝_!; ⋯ 𝑝_! = 𝑘! 𝑝_!; ⋯

Определим показатели эффективности работы многоканальной СМО с отказами:

1. 
   вероятность отказа 𝑝_отк (вероятность того, что все n каналов заняты) равна предельной вероятности состояния 𝑆_!
   

𝜌!

𝑝_отк =𝑝_! =𝑛! 𝑝_!;

2. 
   относительная пропускная способность Q (вероятность того, что заявка будет обслужена)
   

𝜌!

𝑄=1−𝑝_отк =1−𝑛! 𝑝_!;

3. 
   абсолютная пропускная способность A
   

𝜌!

𝐴=𝑄 ∙ 𝜆=𝜆(1−𝑛! 𝑝_!).

4. 
   среднее число занятых каналов k – математическое ожидание числа занятых каналов, которое можно определить по формуле для математического ожидания
   

𝑘_! ∙ 𝑝_!,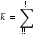

!

𝑘_! – число занятых каналов;

𝑝_! – вероятность 𝑘_! занятых каналов.

Величину 𝑘 можно найти и по формуле

𝐴 𝑄 ∙ 𝜆 𝜌^!

𝑘=𝜇= 𝜇 =𝜌(1−𝑛! 𝑝_!).

Пример 3. Имеется трехканальная телефонная линия. Заявка-вызов поступившая в момент, когда все три канала заняты, получает отказ. Простейший поток заявок поступает с интенсивностью λ = 60 звонков в час. Средняя продолжительность разговора три минуты. Определить показатели эффективности работы СМО.

Решение. Поскольку средняя продолжительность разговора три минуты (3/60 = 0,05 часа), то интенсивность обслуживания заявки будет равна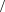

𝜇=1 𝑡обсл =1 0,05=20звоков час .

Тогда приведенная интенсивность потока заявок

𝜆 60

𝜌= = =3.

𝜇 20

Размеченный граф состояний рассматриваемой многоканальной

СМО с отказами можно представить в виде



В начале определим все предельные вероятности состояний СМО. Для этого воспользуемся рассмотренными выше формулами Эрланга:

<sup>𝜌! 𝜌!9 27

𝑝! =</sup>(1+𝜌+2! +3!)^!! =1+3+2+ 6 =0,077;

𝑝_! =𝜌 ∙ 𝑝_! =3 ∙ 0,077=0,231;

𝑝_!

𝑝_! .

Далее определим показатели эффективности работы СМО.

1. 
   вероятность отказа 𝑝_отк (вероятность того, что все 3 канала заняты) равна предельной вероятности состояния 𝑆_!
   

𝑝_отк =𝑝_! =0,346;

2. 
   относительная пропускная способность Q (вероятность того, что заявка будет обслужена)
   

𝑄=1−𝑝_отк =1−0,346=0,654;

3. 
   абсолютная пропускная способность A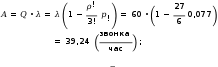
   

4. 
   среднее число занятых каналов 𝑘 – математическое ожидание числа занятых каналов, которое можно определить по формуле для математического ожидания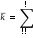
   

𝑘_! ∙ 𝑝_! =0 ∙ 𝑝_!+1 ∙ 𝑝_!+2 ∙ 𝑝_!+3 ∙ 𝑝_! =1,96; !

5. 
   среднее число свободных каналов 𝑙 – математическое ожидание числа свободных каналов (𝑙_!), которое можно определить по формуле для математического ожидания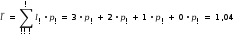
   

.

Сумма среднего числа занятых и свободных каналов должна равняться числу каналов, действительно, 𝑘+ 𝑙 =3.

Одноканальная СМО с неограниченной очередью

Пусть СМО имеет один канал обслуживания, на вход которой поступает простейший поток заявок с интенсивностью λ. Заявки обслуживаются с некоторой интенсивностью µ. Если заявка застала обслуживающий канал занятым, то она встает в очередь и ожидает обслуживания. Никаких ограничений ни по длине очереди, ни по времени ожидания нет.

Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром µ.

Среднее время обслуживания одной заявки 𝑡_обсл =¹𝜇.

Необходимо определить предельные вероятности состояний СМО и показатели ее эффективности.

СМО может находиться в одном из состояний:

𝑆_! – канал свободен;

𝑆_! – канал занят, обслуживает заявку, очереди нет;

𝑆_! – канал занят, обслуживает заявку, в очереди одна заявка;

…

𝑆_! – канал занят, обслуживает заявку, в очереди (k-1) заявка;

…

Размеченный граф состояний рассматриваемой одноканальной СМО с ожиданием можно представить в виде



Это процесс гибели и размножения, но с бесконечным числом состояний.

Для такого процесса, при условии, что приведенная интенсивность потока заявок меньше единицы, т.е. 𝜌^{= !} <1, существуют !

предельные вероятности состояний. Определим эти вероятности. Для этого можно воспользоваться формулами (1), хотя они и были получены для случая конечного числа состояний системы. Тогда для случая одного канала n = 1 можно записать

𝑝_! = 1+𝜌+𝜌^!+⋯+𝜌^!+⋯ ^!!.

Геометрический ряд, стоящий в скобках сходится только при 𝜌<1. Сумма этого ряда стремится к , как сумма ряда со знаменателем меньшим единицы. Поэтому для первого члена прогрессии можно записать

𝑝_! =1−𝜌,

а предельные вероятности состояний 𝑆_! определяются по формулам

𝑝_! =𝜌^! ∙ 𝑝_! = 𝜌^! ∙ 1−𝜌 , 𝑘=1, 2, 3…

Теперь определим показатели эффективности работы одноканальной СМО с ожиданием:

1. 
   среднее число заявок в системе 𝐿_сист определяется по формуле математического ожидания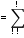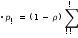
   

𝐿сист𝑘𝑘 ∙ 𝑝!.

!!

Можно показать, что эта формула при 𝜌<1 преобразуется к виду

𝜌

𝐿сист =1−𝜌;

2. 
   среднее число заявок, находящихся под обслуживанием 𝐿_об определяется по формуле математического ожидания
   

𝐿_об =0 ∙ 𝑝_!+1 ∙ 1−𝑝_! =𝜌;

3. 
   среднее число заявок в очереди L_оч определяется как разность между L_сист и L_об
   

𝜌 𝜌^!

𝐿_оч =𝐿_сист −𝐿_об =1−𝜌−𝜌=1−𝜌;

4. 
   среднее время пребывания заявки в системе T_сист равно среднему числу заявок в системе, деленному на интенсивность потока заявок
   

T_сист =𝐿сист𝜆 ;

5. 
   среднее время пребывания заявки в очереди T_оч равно среднему числу заявок в очереди, деленному на интенсивность потока заявок
   

Tоч =𝐿𝜆оч .

Формулы для вычисления T_сист и T_оч называются формулами Литтла.

Пример 4. Имеется магазин с одним продавцом. Предполагается, что простейший поток покупателей поступает с интенсивностью λ = 20 человек/час. Время обслуживания покупателя есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром µ = 25 человек/час. Определить:

1. 
   среднее время пребывания покупателя в очереди;
   
2. 
   среднее число покупателей в очереди;
   
3. 
   среднее число покупателей в магазине;
   
4. 
   среднее время пребывания покупателя в магазине;
   
5. 
   вероятность того, что в магазине не окажется покупателей; 6) вероятность того, что в магазине окажется ровно 4 покупателя.
   

Решение. Рассматриваемый магазин представляет собой одноканальную СМО с ожиданием. Размеченный граф состояний для такой СМО можно представить в виде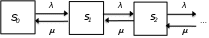



Поскольку

𝜆 20

𝜌= = =0,8<1, 𝜇 25

то существуют предельные вероятности состояний СМО.

Определим требуемые показатели эффективности СМО:

1. 
   Среднее число покупателей в магазине:
   

𝜌 0,8 покупателя

𝐿сист =1−𝜌=0,2=4( час ).

2. 
   Среднее время пребывания покупателя в магазине:
   

𝑇_сист =𝐿^сист𝜆 =20⁴ =0,2 (часа)=12 (минут).

3. 
   Среднее число покупателей в очереди:
   

𝜌^! 0,64

𝐿_оч =1−𝜌= 0,2 =3,2 (человека).

4. 
   Среднее время пребывания покупателя в очереди
   

T_оч =𝐿𝜆^оч =³20^,2=0,16 часа =9, 6 минут .

5. 
   Вероятность того, что в магазине не окажется покупателей равна
   

𝑝_! =1−𝜌=1−0,8=0,2.

6. 
   Вероятность того, что в магазине окажется ровно 4 покупателя равна
   

𝑝_! =𝜌^! ∙ 𝑝_! = 𝜌^! ∙ 1−𝜌 =0,8^! ∙ 0,2=0,082.