Эконометрика. Эконометрика. 18.09. Севостьянова. Занятие по дисциплине эконометрика порядок выполнения задания

• Название: Занятие по дисциплине эконометрика порядок выполнения задания
• Анкор: Эконометрика
• Дата: 07.02.2022
• Размер: 195.27 Kb.
• Имя файла: Эконометрика. 18.09. Севостьянова.docx
• Тип: Занятие; #353813

Ксения Севостьянова. СПБ19-1Б-ЭК01.

ЗАДАНИЕ НА СЕМИНАРСКОЕ ЗАНЯТИЕ ПО ДИСЦИПЛИНЕ ЭКОНОМЕТРИКА

Порядок выполнения задания:

2.Выполнить лабораторные работы № 1 и 2 на стр. 11:

-построение линии регрессии проводить с помощью поля корреляции;

-подбор наиболее достоверного уравнения проводить также с помощью поля корреляции.

3.Отчет по выполненной работе представить в следующей форме:

-условие задания;

-скриншоты с Excel всех расчетов в соответствии с пунктами задания;

-выводы по работе.

Лабораторная работа № 1

Задание. На основании данных табл. П1 для соответствующего варианта (табл. 1.1):

1. Вычислить линейный коэффициент парной корреляции.

2. Проверить значимость коэффициента парной корреляции.

3. Построить доверительный интервал для линейного коэффициента парной корреляции

Условие задания:

Наличие предметов длительного пользования в домашних хозяйствах по регионам Российской Федерации (европейская часть территории без республик Северного Кавказа) (по материалам выборочного обследования бюджетов домашних хозяйств; на 100 домохозяйств; штук)

Севостьянова вариант 12, поэтому у меня 1 столбец (телевизоры) и 5 столбец (персональные компьютеры).

По исходным данным составим табл.1.1

1. 
   Далее мы находим линейный коэффициент парной корреляции с помощью Анализа данных.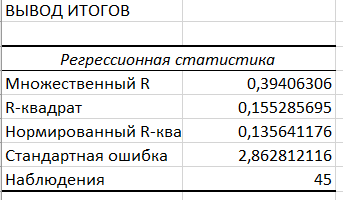
   

Линейный коэффициент парной корреляции равен 0,39406306 или множественному R

Вывод: как мы знаем из свойств линейного парного коэффициента корреляции: если коэффициент больше 0,3 и меньше 0,7, то связь между наличием телевизоров и персональных компьютеров в домашних хозяйствах регионов Российской Федерации — умеренная

2. 
   Следующее, что нам необходимо найти будет значимость коэффициента парной корреляции.
   

Проверим коэффициент парной корреляции на уровне значимости, то есть с вероятностью ошибки 5%. Выдвигаем гипотезы:
H0: p_xy =0, т.е. отсутствует линейная зависимость между х и у.
Н1: p_xy ≠0, т.е. существует линейная зависимость между х и у.
Используется t-критерий Стьюдента.

Рассчитываем наблюдаемое значение критерия:

Чтобы найти t_кр, нам нужно воспользоваться функцией СТЬЮДРАСПОБР(α;n-2), где

α- вероятность ошибки, (в функцию вводим 0,05)

n-кол-во наблюдений (эти данные можно взять с регрессионной статистики)

Для нахождения t_набл воспользуемся формулой, где k =n-2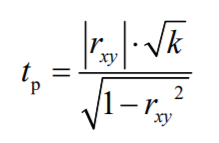



Тогда t_кр и tнабл равны:





Также итог t_набл мы можем проверить в уже готовом анализе данных в t-статистике



Т.е. мы можем сделать вывод, что расчет по формуле проведен верно.

Вывод: Если t_набл > t_кр, то гипотеза H₀ отвергается с вероятностью ошибки меньше чем 5%. Это свидетельствует о значимости линейного коэффициента корреляции r_ху и статистической существенности зависимости между факторным и результативным признаками.

3. 
   Построим доверительный интервал для линейного коэффициента корреляции, используя выражение:
   

Находим доверительный интервал с помощью формулы:




Т. е. истинное значение парного линейного коэффициента корреляции находится в пределах от 0,140116 до 0,64801.

ВЫВОД ПО РАБОТЕ:

В данной лабораторной работе были разобраны темы линейного коэффициента парной корреляции, значимость этого коэффициента и доверительный интервал. Доверительный интервал показал, что в ходе лабораторной работы вычисления были сделаны правильно, значимость коэффициента подтвердилась.

Лабораторная работа № 2

Задание. На основании данных табл. П1 для соответствующего варианта (табл. 1.1):

Виды кривых выравниваний по 12 варианту: линейная, показательная, логарифмическая.

1. 
   Построить предложенные уравнения регрессии, включая линейную регрессию.
   

По исходным данным необходимо построить уравнения регрессии. Мы делаем это в Экселе с помощью точечной диаграммы, а также добавляя линии тренда по заданному варианту.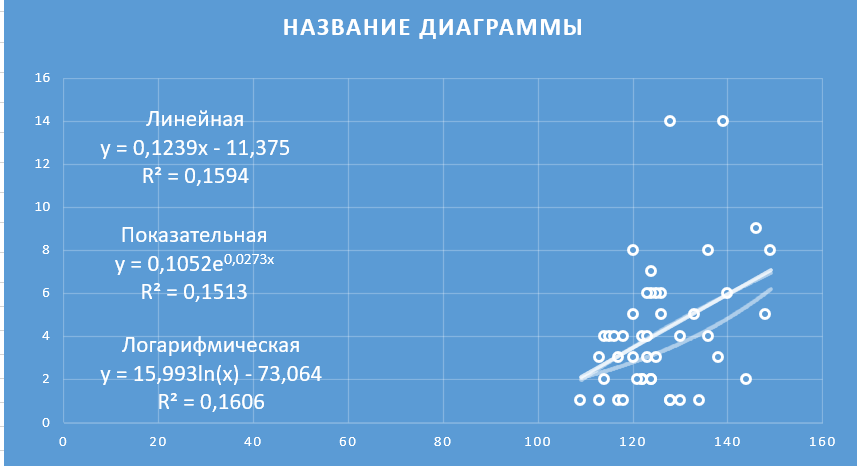



На диаграмме четко прослеживаются все заданные уравнения регрессий.

2. 
   Вычислить индексы парной корреляции для каждого уравнения.
   

Далее необходимо найти индексы.

Для линейной регрессии мы находили ранее. Для нелинейных же требуется использовать формулу: уже данный в диаграмме квадрат индекса детерминации возвести в корень.

3. 
   Проверить значимость уравнений регрессии и отдельных коэффициентов линейного уравнения.
   

С помощью функции СТЬЮДРАСП находим требуемое задание.

4. 
   Определить лучшее уравнение регрессии на основе средней ошибки аппроксимации.
   

Следующее задание снова возвращает нас к величине достоверности аппроксимации.

Данная величина также является показателем средней ошибки аппроксимации. Чем больше R2, тем лучше уравнение регрессии.



По данной таблице видно, что лучшим уравнение регрессии является логарифмическое уравнение.

5. 
   Определить средний коэффициент эластичности.
   

С помощью функции Линейн Для расчёта параметров уравнения линейной регрессии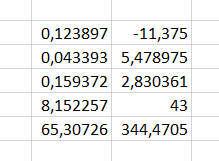



Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле: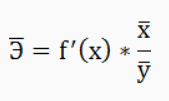



По функции СрЗнач находим средние значения столбца В и С и вставляем в формулу, показанную выше



Таким образом, при изменении зависимости персональных компьютеров от телевизоров на 1% от своего среднего значения кол-во персональных компьютеров изменится в среднем на 3,7%.

ВЫВОД

1. В ходе лабораторной работы были построены уравнения регрессии трех видов: Линейное, показательное и логарифмическое.

4. При построении интервального прогноза для значения x = x_max по уравнению линейной регрессии, оба уравнения лежат в положительном интервале.

5. Средний коэффициент эластичности показал, что в линейной регрессии на 3,7% в среднем по совокупности изменится результат y от своей величины при изменении фактора x на 1% от своего значения.