геодэзические задачи. ПЗ 2 Прямая и обратная геодезиченские задачи. Занятие прямая и обратная геодезическая задачи
 Скачать 143.38 Kb. Скачать 143.38 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2. ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧИ Цель работы: научиться решать прямую и обратную геодезические задачи на плоскости. Общие сведения Прямая геодезическая задача состоит в том, чтобы определить координаты конечной точки Х2, У2 по известным координатам начальной точки Х1, У1, горизонтальному проложению s 1-2 и дирекционному углу α 1-2. Рассмотрим наиболее простой случай, когда горизонтальное проложение АВ находится в I четверти и имеет северо-восточное направление и румб линии равен значению дирекционного угла (рис. 2.1). 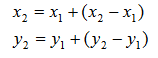 Приращение координат линии – ортогональная проекция горизонтального проложения этой линии на оси ординат, их обозначают Δх и Δу: 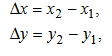 Тогда 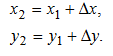 Приращения координат могут быть вычислены по дирекционному углу линии и ее горизонтальному проложению, являющемуся гипотенузой прямоугольного треугольника, в котором катеты – приращения координат и вычисляются по формулам: 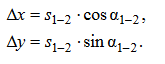 Приращения координат имеют знаки плюс или минус, в зависимости от знака косинуса или синуса дирекционного угла. При переходе от дирекционных углов к румбам: 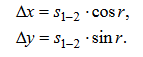 В связи с тем, что значения тригонометрических функций всегда положительны, cos r и sin r, т.к. r ≤ 90°, знаки приращений координат определяют в соответствии с названиями румбов. Обратная геодезическая задача состоит в том, чтобы вычислить горизонтальное проложение s 1-2 и дирекционный угол α 1-2 по известным координатам начальной (Х1, У1) и конечной (Х2, У2) точек. 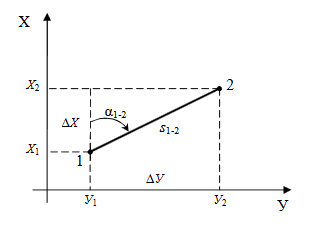 Рис. 2.1. Схема решения прямой и обратной геодезических задач на плоскости По катетам прямоугольного треугольника, т.е. приращениям координат, можно вычислить дирекционный угол: 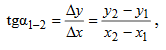 тогда, Горизонтальное проложение s 1-2 вычисляют по формулам: 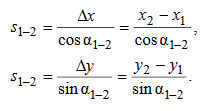 Эту же задачу можно решить другим способом: Искомый дирекционный угол α1-2 вычисляется по формулам 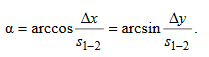 Задания 1. Определить прямоугольные координаты точки В, если координаты точки А: хА=6163173,43, уА=9492631,12, αАВ=318°47', sAB=673,56 м 2. Вычислить дирекционный угол αCD и горизонтальное проложение sCD, если прямоугольные координаты точек C и D составляют хC = 6319281,1, уC = 9 540014,2; xD = 6323061,6, yD = 9542229,7 м. Порядок выполнения работы Задание 1. При решении прямой геодезической задачи значения приращений координат можно вычислить при помощи таблиц натуральных значений тригонометрических функций. При решении прямой геодезической задачи с использованием таблиц натуральных значений тригонометрических функций сначала записывают исходные данные αАВ (п/п 1), sАВ (п/п 2), xА (п/п 3), yА (п/п 4) (табл. 2.2). Затем из таблиц натуральных значений тригонометрических функций находят значение cosαАВ и sinαАВ. Далее вычисляют ΔxАВ и ΔyАВ, отрицательный знак зависит от sin318°47' (IV четверть). Далее, прибавляя к координатам точки А приращения координат, вычисляют координаты точки В. Рабочие формулы: 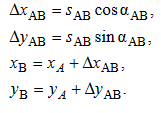 Таблица 2.2. Решение прямой геодезической задачи 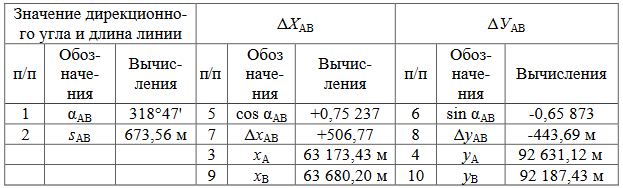 Для контроля вычисленных приращений пользуются формулой: Допустимые отклонения составляют 0,01-0,02 м. 2. При решении обратной геодезической задачи при помощи таблиц натуральных значений тригонометрических функций сначала выписывают координаты исходных пунктов (табл. 2.3). Рабочие формулы: 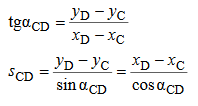 Таблица 2.3. Решение обратной геодезической задачи 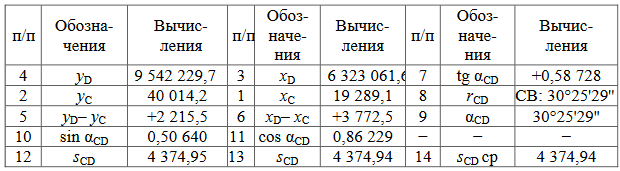 Затем вычисляют разности координат и определяют значение tgα. Пользуясь таблицами натуральных значений тригонометрических функций и учитывая знаки приращений координат, по величине tgα вначале определяют румб искомого направления, а затем и дирекционный угол. Далее, определив значения sinα и cosα дважды вычисляют значения искомой стороны, как частное от деления (п/п 5 и п/п 10) и (п/п 6 и п/п 11). Расхождение должно быть не более одной единицы пятого знака. Среднее значение из двух делений принимается за окончательное. Контрольные задания для самостоятельной работы Таблица 2.4Данные задания для самостоятельной работы 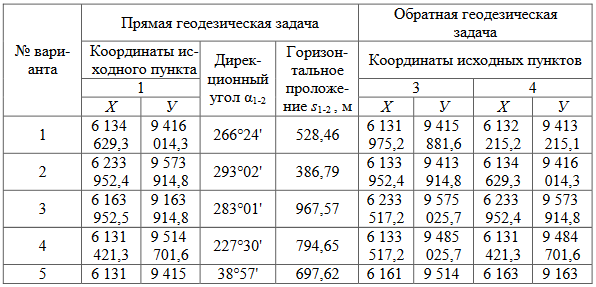 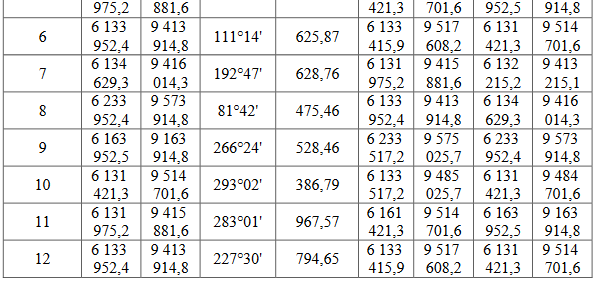 |
