Защищен с оценкой
 Скачать 0.6 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ» КАФЕДРА №5 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ РУКОВОДИТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2022 Цель: изучить парную линейную регрессию и корреляцию при помощи Excel. Вариант 5 Таблица 1. Исходные данные 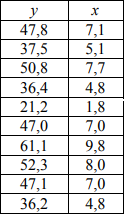   Таблица 2. Средние значения.
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических yt минимальна (yt – теоретическое значение результативного признака, найденное исходя из уравнения регрессии).  = 𝑐𝑜𝑣(𝑥, 𝑦) 𝑦 ∗ 𝑥 − 𝑦 ∗ 𝑥 𝑏 =     𝜎 𝑥 2 𝑥 2 − 𝑥2 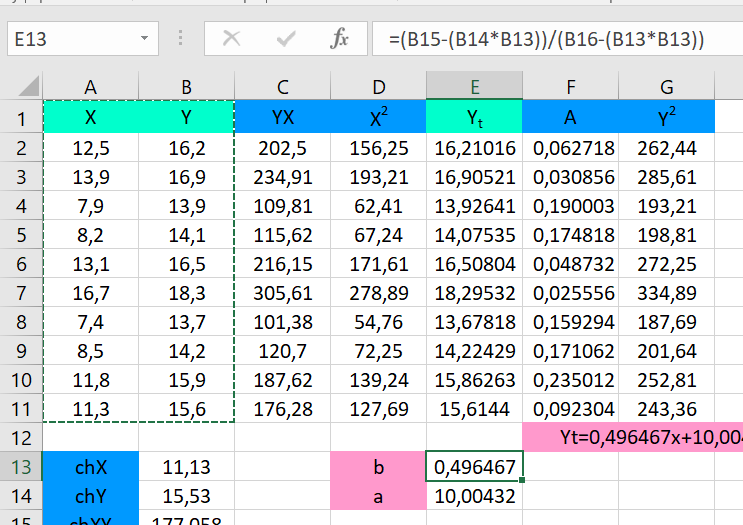 Рисунок 1. Вычисления параметра b. 𝑎 = 𝑦̅ − 𝑏𝑥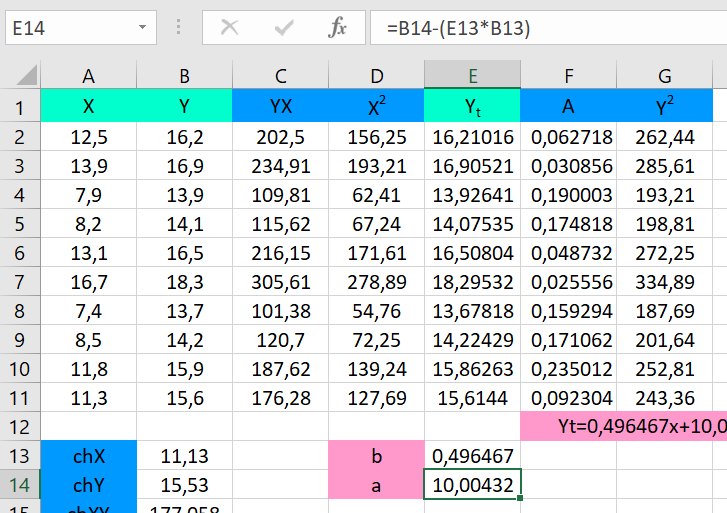 Рисунок 2. Вычисления параметра a. После получения параметров a и b, получаем уравнение: 𝑦𝑡 = 0,496467𝑥 + 10,00432 С его помощью получаем yt относительно данных x и строим график: 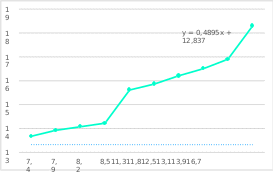 Рисунок 3. График зависимости yt от x. Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических.   𝐴 = 1 ∑ |𝑦 − 𝑦𝑡 | ∗ 100, %𝑛 𝑦 𝐴 = 0,119035   Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rxy. Для линейной регрессии ( −1 ≤ rxy ≤ 1), причем, если коэффициент регрессии b > ,0 то 0 ≤ rxy ≤1 и, наоборот, при b < 0, −1 ≤ rxy ≤ 0. √𝑥2 − (𝑥)2  𝑟𝑥𝑦 = 𝑏 √𝑦2 − (𝑦)2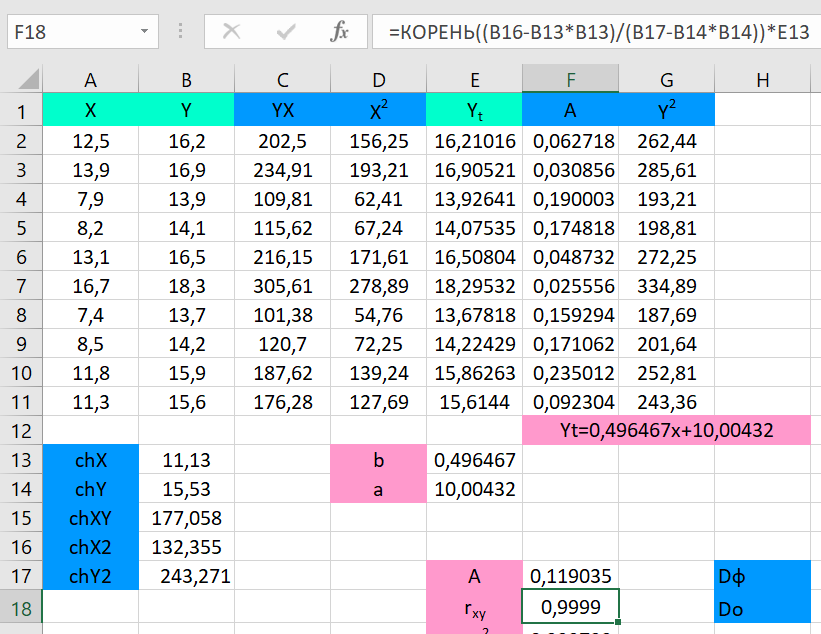 Рисунок 4. Вычисления параметра rxy. Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.  xy Коэффициент детерминации (квадрат линейного коэффициента корреляции r 2) характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака: 𝑟2 = 𝜎2 𝜎 𝑦объясн =  ∑(𝑦𝑡 − 𝑦)2  𝑥𝑦 2 𝑦общ ∑(𝑦 − 𝑦)2 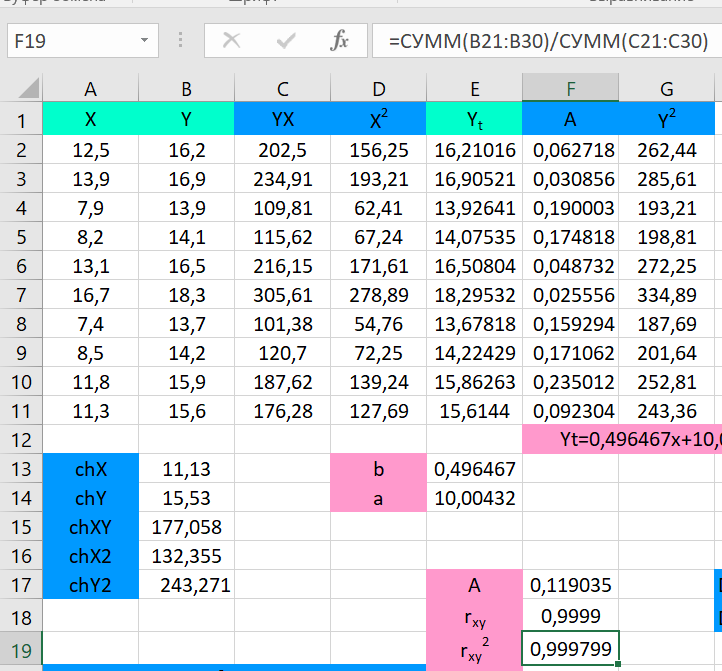 Рисунок 5. Вычисления параметра rxy2.  Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины y при изменении фактора х на 1% от своего среднего значения: 𝑥 Э = 𝑓′(𝑥) 𝑦 Э = 0,355807 Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D. ∑(𝑦 − 𝑦)2𝐷общ = 𝐷факт =  𝑛 − 1 ∑(𝑦𝑡 − 𝑦)2 𝑛 − 1 𝐷ост = ∑(𝑦 − 𝑦𝑡)2 𝑛 − 2 Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия для проверки нулевой гипотезы.𝐹 = ∑(𝑦𝑡 − 𝑦)2/𝑚 2   𝑟 = 𝑥𝑦   1 − 𝑟 1 ∑(𝑦 − 𝑦𝑡)2 /(𝑛 − 𝑚 − 1) 2 𝑥𝑦 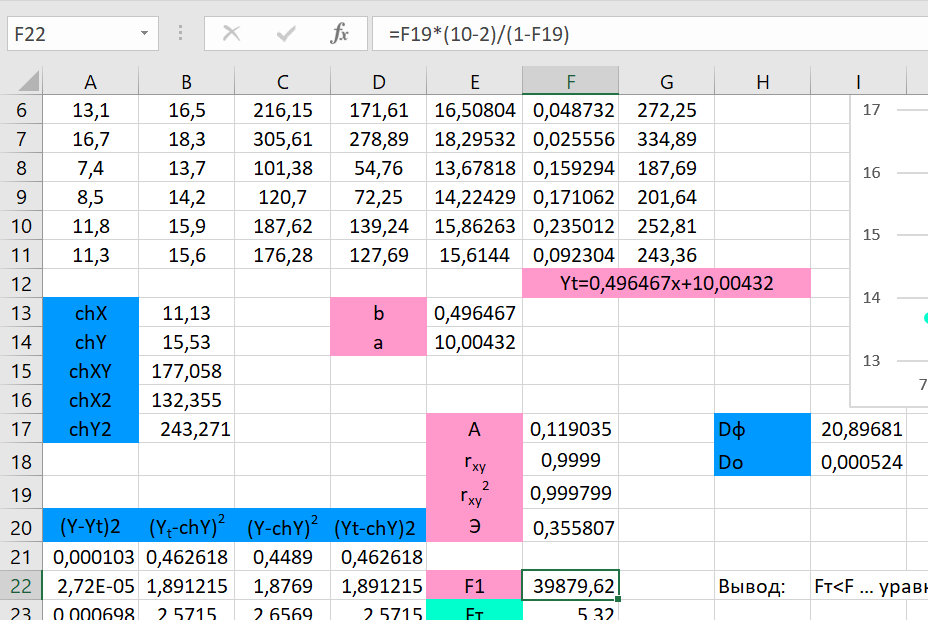 Рисунок 6. Вычисления параметра F1. 𝐷факт 𝐹2 =  𝐷ост 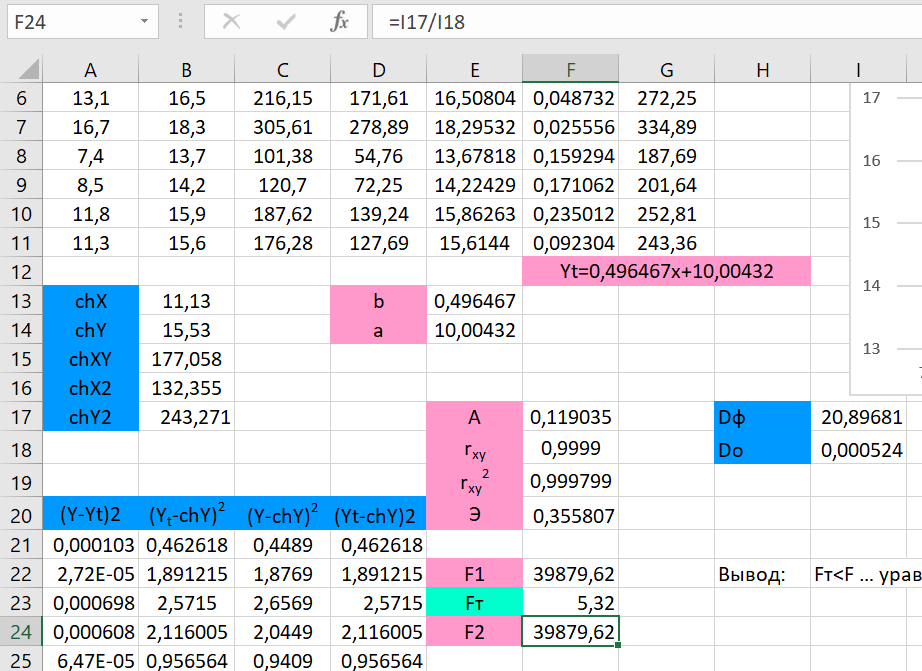 Рисунок 7. Вычисления параметра F2. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Фактическое значение F-критерия Фишера сравнивается с табличным значением Fтабл(α; k1; k2) при уровне значимости α и степенях свободы k1=m и k2=n-m-1. Fтабл = 5,32 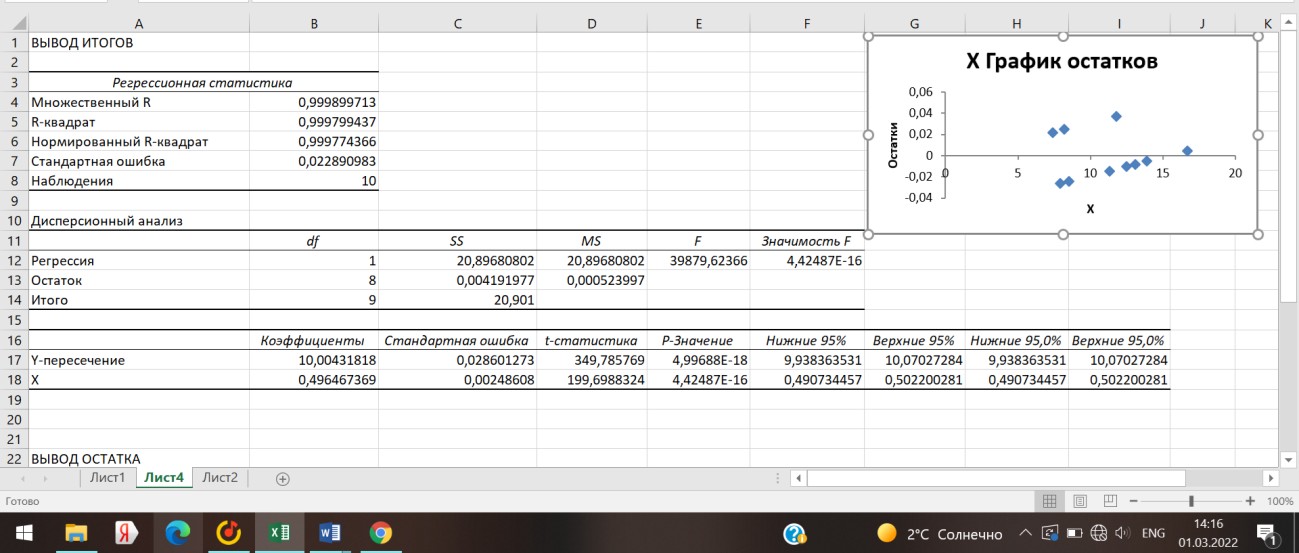 Рисунок 8. Результат применения инструмента регрессия. 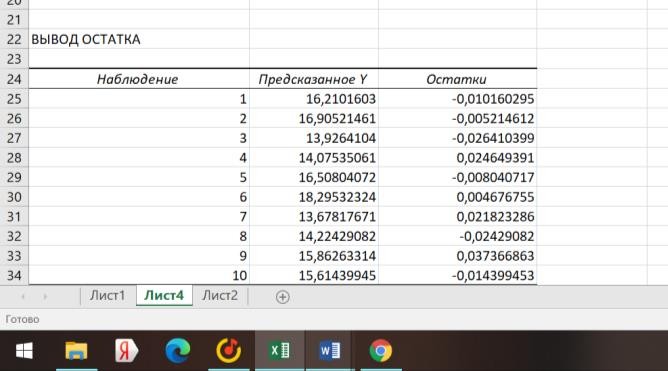 Рисунок 9. Результат применения инструмента регрессия. Вывод: В ходе проведенной лабораторной работы были произведены расчеты нескольких показателей: теоретическое значение результативного признака, линейный коэффициент парной корреляции, коэффициент детерминации, средняя ошибка аппроксимации, средний коэффициент эластичности, критерий Фишера. Качество построенной модели хорошее, так как средняя ошибка аппроксимации не превышает 8-10%. Полученные данные были проверены с помощью функции ЛИНЕЙН и инструмента анализа данных Регрессия в программе Excel. Так же было установлено, что табличное значение F-критерия больше табличного значения, из чего следует, что уравнение статистически значимо. |