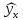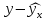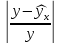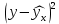Вариант 3. Задача По территории региона приводятся данные за 199Х год Номер региона
 Скачать 285.93 Kb. Скачать 285.93 Kb.
|
|
Контрольная работа по эконометрике Вариант 3 Задача 1.По территории региона приводятся данные за 199Х год
Требуется: 1. Построить линейное уравнение парной регрессии y по x. 2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации. 3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента 4. Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. 5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6. На одном графике отложить исходные данные и теоретическую прямую. Решение 1. Построим линейное уравнение парной регрессии y по x. Ищем уравнение в виде: у = а+ bх. Составим расчетную таблицу для дальнейшего исследования:
Вычислим параметры линейного уравнения регрессии по формулам: 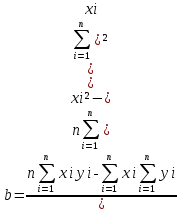 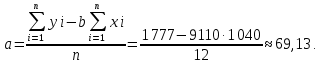 Получено выборочное уравнение линейной регрессии 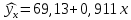 . .2. Рассчитаем линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации. Вычислим линейный коэффициент корреляции по формуле: 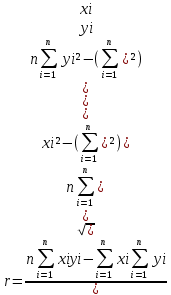 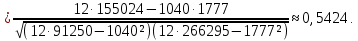 Значение коэффициента корреляции не очень близко к 1, что свидетельствует об умеренной линейной положительной связи (с ростом х значения у возрастают). Коэффициент детерминации r2 = 0,54242 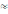 0,2941. 0,2941.Это означает, что 29% вариации заработной платы ( 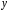 ) объясняется вариацией фактора ) объясняется вариацией фактора 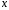 – среднедушевого прожиточного минимума. – среднедушевого прожиточного минимума.Качество модели определяет средняя ошибка аппроксимации: Коэффициент аппроксимации определим по формуле: 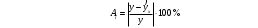 Средняя ошибка аппроксимации: 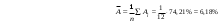 Допустимый предел значений 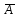 – не более 10 %. – не более 10 %.Качество построенной модели оценивается как хорошее, так как 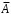 не превышает 8-10%. не превышает 8-10%.3. Оценим статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента. Проведем оценку качества уравнения регрессии в целом с помощью F-критерия Фишера. Найдем фактическое значение F-критерия: 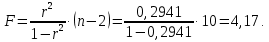 Табличное значение ( 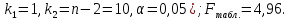 Так как 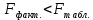 , поэтому уравнение статистически не значимо. , поэтому уравнение статистически не значимо. Оценку статистической значимости параметров регрессии проведем с помощью 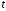 -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей. -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.Табличное значение 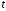 -критерия для числа степеней свободы -критерия для числа степеней свободы 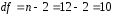 и и 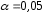 составит составит 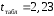 . .Определим случайные ошибки 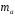 , , 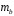 , , 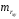 : :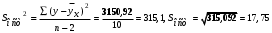 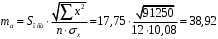 ; ;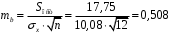 ; ;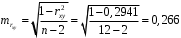 . .Тогда 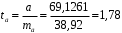 ; ;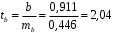 ; ;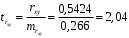 . .Фактические значения 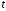 -статистики превосходят табличное значение: -статистики превосходят табличное значение: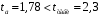 ; ; 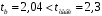 ; ; 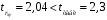 , ,поэтому параметры 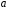 , , 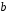 и и 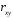 случайно отличаются от нуля и статистически незначимы. случайно отличаются от нуля и статистически незначимы.Рассчитаем доверительные интервалы для параметров регрессии 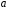 и и 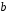 . Для этого определим предельную ошибку для каждого показателя: . Для этого определим предельную ошибку для каждого показателя: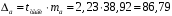 ; ;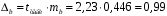 . .Доверительные интервалы 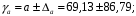 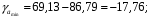 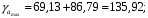 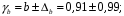 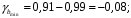 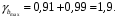 Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 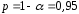 параметры параметры 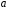 и и 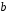 , находясь в указанных границах, принимают нулевые значения, т.е. являются статистически незначимыми и несущественно отличны от нуля. , находясь в указанных границах, принимают нулевые значения, т.е. являются статистически незначимыми и несущественно отличны от нуля.Вывод: статистически незначимы параметры уравнения регрессии и коэффициент корреляции. 4. Выполним прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. Вычислим прогнозное значение результативного фактора 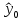 при значении признака-фактора при значении признака-фактора 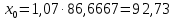 (руб) (руб)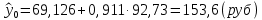 . .5. Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Рассчитаем доверительный интервал прогноза. Ошибка прогноза 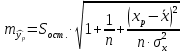 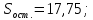 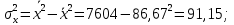 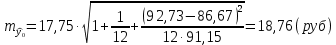 Доверительный интервал рассчитывается так: 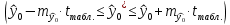 Табличное значение t-критерия Стьюдента при α=0,05 и числе степеней свободы k=n-2=10 есть 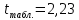 Поэтому доверительный интервал будет иметь вид: 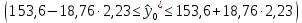 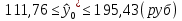 Выполненный прогноз среднемесячной заработной платы является надежным ( 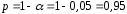 ) и находится в пределах от 111,76 руб. до 195,43 руб. ) и находится в пределах от 111,76 руб. до 195,43 руб.В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую: 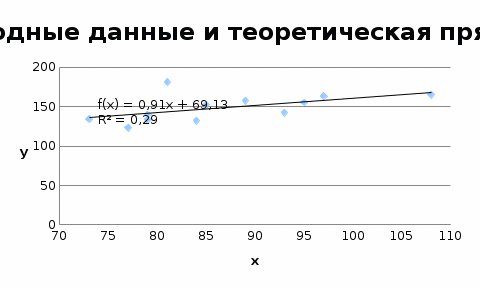 Задача 2. По предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x1 ( от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x2 (%)
Требуется: 1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат 2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их 3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 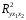 . .5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1. 6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор. |