Расчет стержней. Затем проверить прочность ступенчатого
 Скачать 312.49 Kb. Скачать 312.49 Kb.
|
Задача 1РАСЧЁТ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЁСТКОСТЬ ПРИ РАСТЯЖЕНИИ И СЖАТИИ Вариант 3 Даны схемы брусьев, работающих на растяжение или сжатие. Требуется построить эпюры продольных сил N. Затем проверить прочность ступенчатого бруса (принять F=0,01С2, Свзять из таблицы 1); Построить эпюры перемещений поперечных сечений брусьев. Материал – сталь 3 (Е = 2х105 МПа). Принять [σ] = 160 МПа. Исходные данные: F = 0,0009 м2; P = 30 кН; l = 0,12 м; [σ] = 160 МПа; Е = 2х105 МПа. 1. Вычертим схему бруса в масштабе с указанием числовых значений размеров и действующих нагрузок (рисунок 1). 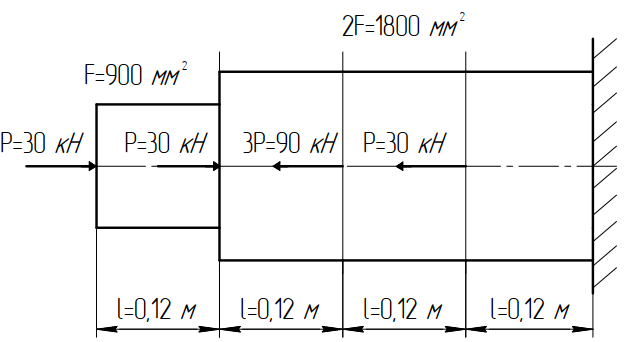 Рисунок 1 – Схема бруса 2. Разобьем брус на участки и пронумеруем их (рисунок 2). 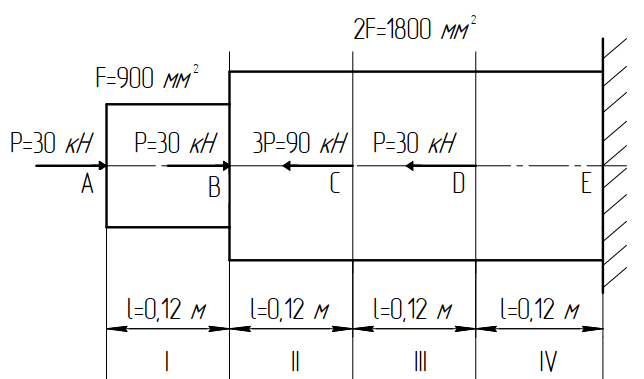 Рисунок 2 – Нумерация участков 3. Определим продольные силы. Участок I: 0 ≤ z1 ≤ 0,12. 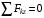 , или , или 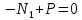 , откуда , откуда 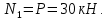 Участок II: 0,12 ≤ z2 ≤ 0,24. 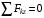 , или , или 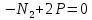 , откуда , откуда 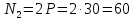 кН. кН.Участок III: 0,24 ≤ z3 ≤ 0,36. 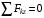 , или , или 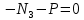 , откуда , откуда 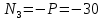 кН. кН.Участок IV: 0,36 ≤ z4 ≤ 0,48. 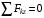 , или , или 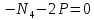 , откуда , откуда 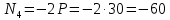 кН. кН.По полученным значениям стоим эпюру продольных сил (рисунок 3). 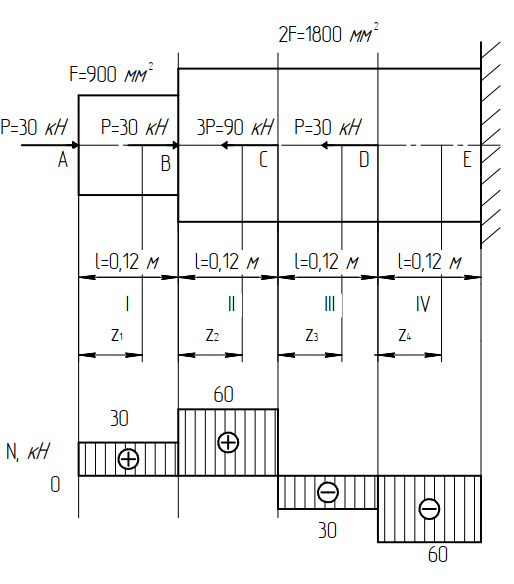 Рисунок 3 – Эпюра продольных сил 4. Нормальные напряжения на участке AB 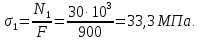 Нормальные напряжения на участке BC 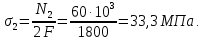 Нормальные напряжения на участке CD 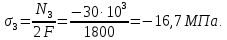 Нормальные напряжения на участке DE 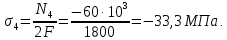 Проверим брус на прочность: 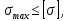 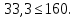 Из результата можем сделать вывод, что брус прочный. 5. По полученным значениям строим эпюру нормальных напряжений (рисунок 4). 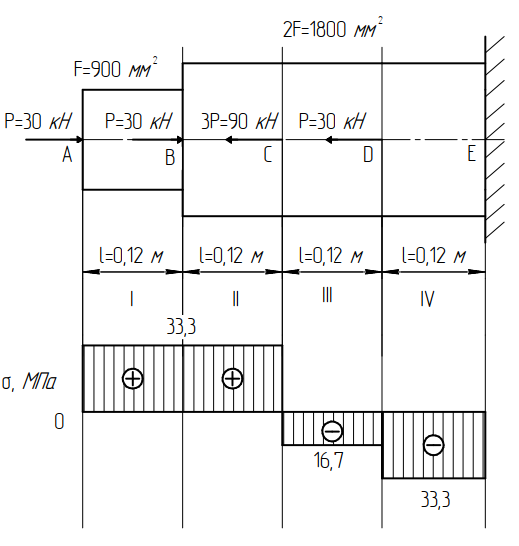 Рисунок 4 – Эпюра нормальных напряжений 6. Вычислим абсолютные деформации участков. Деформация участка AB: 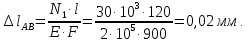 Деформация участка BC: 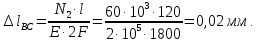 Деформация участка CD: 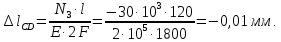 Деформация участка DE: 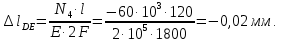 7. Т.к. точка E жестко закреплена, то перемещение сечения E 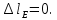 Перемещение сечения D 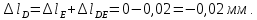 Перемещение сечения C  Перемещение сечения B  Перемещение сечения A  По полученным значениям стоим эпюру перемещений поперечных сечений балки (рисунок 5).  Рисунок 5 – Эпюра перемещений поперечных сечений Задача 2РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ БАЛКИ НА ДВУХ ОПОРАХ Вариант 3 Для балки на двух опорах построить эпюры Qи М. Подобрать двутавровое, кольцевое, прямоугольное, круглое сечения балок. Двутавровое сечение проверить на жесткость. Исходные данные: P = 30 кН; q = 30 кН/м; a = 2 м; [σ] = 160 МПа; [τ] = 100 МПа; d/D = 0,9; h/b = 2. 1. Вычертим схему балки и расставим реакции связей (рисунок 6). 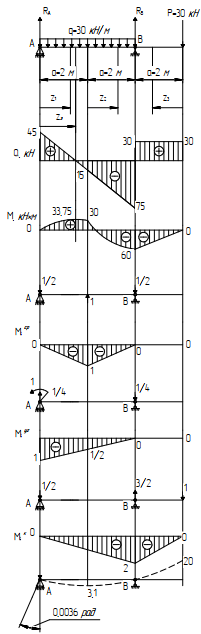 Рисунок 6 – Схема балки и эпюры 2. Определение реакций связей 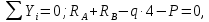 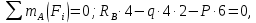 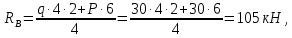 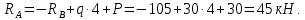 Проверка: 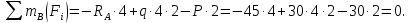 3. Построение эпюр Q и М. Для основного нагруженного состояния разобьем балку на три участка для удобства определения прогиба в середине пролета интегралом Мора. Участок 1: 0 ≤ z1 ≤ 2 м. 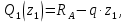 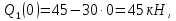 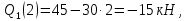 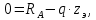 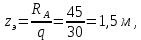 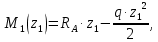 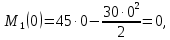 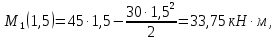 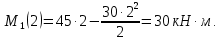 Участок 2: 0 ≤ z2 ≤ 2 м. 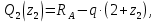 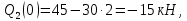 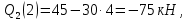 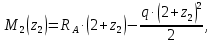 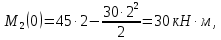 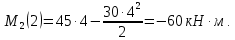 Участок 3: 0 ≤ z3 ≤ 2 м. 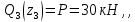 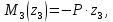 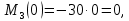 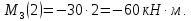 4. Подбор сечений. Из эпюр изгибающих моментов и поперечных сил находим максимальные по модулю значения: 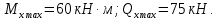 Условие прочности: 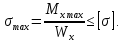 1) Двутавровое сечение. 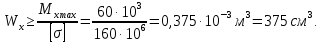 Выбираем из сортамента двутавр № 27а. 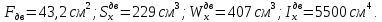 2) Кольцевое сечение (d/D = 0,9). 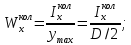 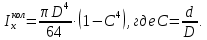 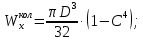 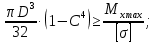 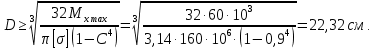 Принимаем D = 22,4 см. 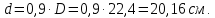 Принимаем d = 20,1 см. 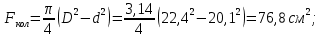 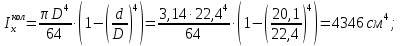 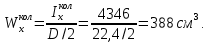 3) Прямоугольное сечение (h/b = 2). 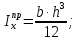 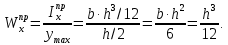 Так как b = h/2 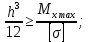 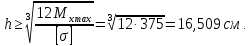 Принимаем h =16,5 (см). Тогда b = h/2 = 16,5/2 = 8,25 см, принимаем b = 8,3 см. 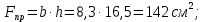 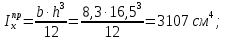 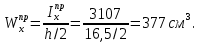 4) Круглое сечение. 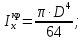 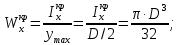 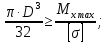 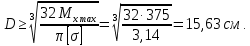 Принимаем D = 15,7см. 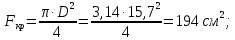 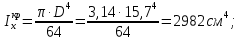 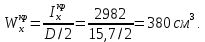 5. Построение эпюр σ и τ. 1) Двутавровое сечение: 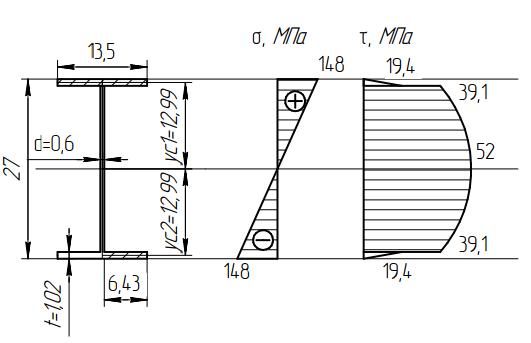 Рисунок 7 – Эпюры напряжений для двутаврового сечения 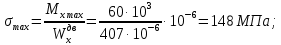 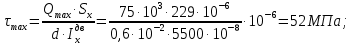 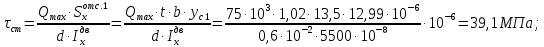  2) Кольцевое сечение:  Рисунок 8 – Эпюры напряжений для кольцевого сечения   3) Прямоугольное сечение: 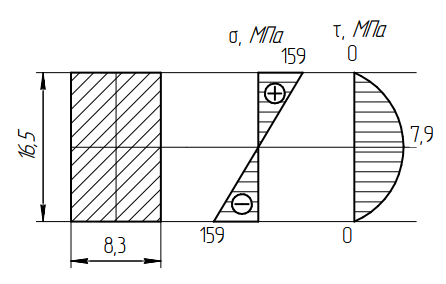 Рисунок 9 –Эпюры напряжений для прямоугольного сечения 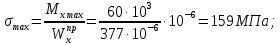 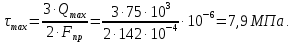 4) Круглое сечение: 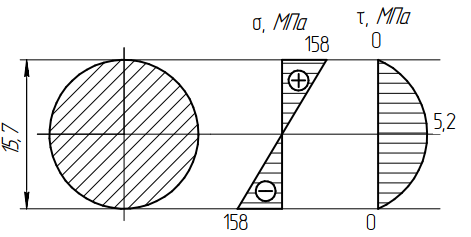 Рисунок 10 – Эпюры напряжений для круглого сечения 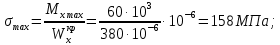 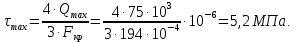 6. Сравнительная оценка сечений по отношению к двутавровому. 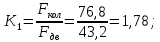 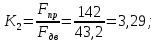  7. Определение прогиба в середине пролета ∆С и угла поворота θА на левой опоре. 1) Определение прогиба в середине пролета ∆С. Для определения прогиба необходимо построить единичную эпюру  от единичной силы. от единичной силы. Участок 1: 0 ≤ z1 ≤ 2 м.  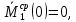 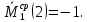 Участок 2: 0 ≤ z2 ≤ 2 м. 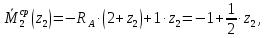 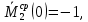 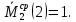 Участок 3: 0 ≤ z3 ≤ 2 м. 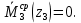 Интеграл Мора: 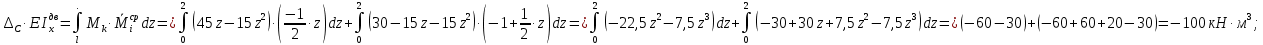 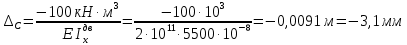 2) Определение угла поворота на левой опоре θА. Для определения угла поворота необходимо построить единичную эпюру 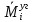 от единичного момента. от единичного момента.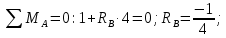 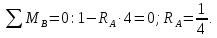 Участок 1: 0 ≤ z1 ≤ 4 м. 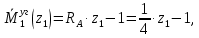 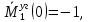 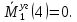 Участок 2: 0 ≤ z2 ≤ 2 м. 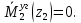 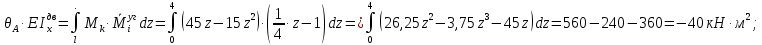 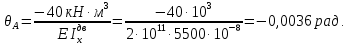 8. Проверка прогиба и угла поворота из пункта 7 приемом Верещагина. Вычисление прогиба ∆С приемом Верещагина: 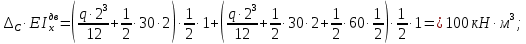 Вычисление угла поворота θА приемом Верещагина: 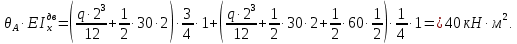 Для определения прогиба конца консоли ∆к необходимо построить единичную эпюру 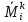 от единичной силы: от единичной силы: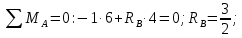 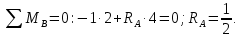 Участок 1: 0 ≤ z1 ≤ 4 м. 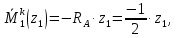 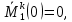 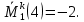 Участок 2: 0 ≤ z2 ≤ 2 м. 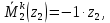 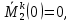 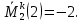 Воспользуемся приемом Верещагина для определения прогиба конца консоли ∆к: 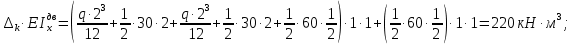 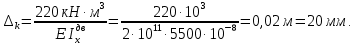 9. Проверка балки на жесткость по прогибу. В середине пролета: 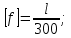 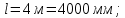 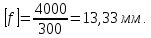 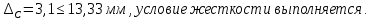 Конец консоли: 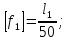 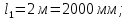    |
