ДОКЛАД ПО ГЕОМЕТРИИ. Звездчатые многогранники
 Скачать 83.5 Kb. Скачать 83.5 Kb.
|
|
ДОКЛАД ПО ГЕОМЕТРИИ НА ТЕМУ «ЗВЕЗДЧАТЫЕ МНОГОГРАННИКИ» Работу выполнили Ученицы 9 класса «Г» МБОУ СОШ № 98 Г.Краснодара Невежина Виктория и Карслян Вероника Учитель : Кардашевский Борис Константинович ЗВЕДЧАТЫЕ МНОГОГРАННИКИ Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у не звёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами. Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам. Правильные звёздчатые многогранники - это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера-Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера-Пуансо. ЗВЕЗДЧАТЫЙ ОКТАЭДР Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера». По сути она является соединением двух тетраэдров. Звёздчатый октаэдр можно было бы признать правильным многогранником, так как все его грани - правильные треугольники одинакового размера и все углы между ними равны. Но на самом деле это геометрическое тело не является шестым правильным многогранником на равне с пятью известными Платоновыми телами. Причина в том, что в определении правильного многогранника присутствует слово выпуклый, то есть все грани должны лежать по одну сторону от плоскости, проходящей через любую из них. Звездчатый додекаэдр Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр (звёздчатый большой додекаэдр, завершающая форма). Первые две из них были открыты Кеплером (1619), третья — Пуансо (1809). В отличие от октаэдра любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник. Все 3 звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников. У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани - пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3. (малый звёздчатый додекаэдр большой додэкаэдр большой звездчатый додекаэдр) Малый звездчатый додекаэдр - Продолжение ребер додекаэдра приводит к замене каждой грани звездчатым правильным пятиугольником, и в результате возникает многогранник, который называется малым звездчатым додекаэдром. Этот многогранник можно также получить из додекаэдра, установкой на его гранях правильных пятиугольных пирамид. Большой звездчатый додекаэдр - Этот многогранник получается при продолжении граней додекаэдра. При этом каждая грань заменяется на правильный звездчатый пятиугольник.Его можно также получить из икосаэдра, установкой на его гранях правильных треугольных пирамид. ЗВЕЗЧАТЫЙ ИКОСАЭДР Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окруженовеликим многообразием отсеков – частей пространства, ограниченных плоскостями граней. Все звездчатыеформы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+20+60+120+ 12+30+60+60 отсеков десятиразличных форм и размеров. Большой икосаэдр (см. рис) состоит из всех этих кусков, за исключениемпоследних шестидесяти. Среди звёздчатых форм икосаэдра встречаются некоторые соединения платоновых тел. Среди них:соединения пяти октаэдров, энантиоморфные формы соединения пяти тетраэдров и соединения десятитетраэдров. Если бы Платон смог видеть эти формы, они привели бы его в восхищение. После того как былиоткрыты эти и ряд других многогранников, ученые, естественно, задумались над вопросом: сколькосуществует звездчатых форм икосаэдра? В 1900 году Брюкнер опубликовал классическую работу омногогранниках, озаглавленную "Vielecke und Vielflache", в которой были представлены некоторые новыезвездчатые формы икосаэдра. Открытием еще несколько форм мы обязаны Уиллеру(1924). В 1938 годусистематическое и полное исследование вопроса провел Кокстер совместно с Дювалем, Флэзером, Петри. Для различения исходных форм и выделения характерных форм они применили правила ограничения, установленные Дж. Миллером. Кокстер доказал, что существует всего 59 звездчатых форм икосаэдра, изкоторых 32 обладают полной, а 27 неполной икосаэдральной симметрией (последнее обстоятельство даетвозможность строить энантиоморфные им аналоги, которые имеют красивый и необычный вид). 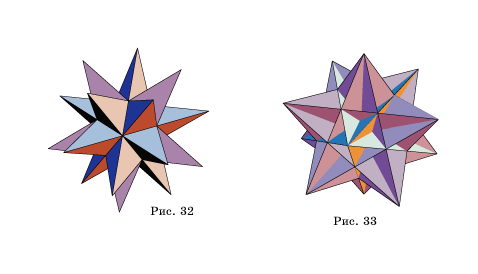 ЗВЕЗДЧАТЫЕ КУБООКТАЭДРЫ Звёздчатый кубооктаэдр (кубооктаэдр) – полуправильный многогранник.В кубе проводятся отсекающие плоскости через середину ребер, выходящих из одной вершины. В результате получится полуправильный многогранник - кубооктаэдр. Его гранями являются шестьквадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название. Квадратные грани группируются в пары таким образом, что грани каждой из них параллельны между собойи перпендикулярны к остальным подобным граням. Многогранник представляет собой своего рода соединение шести четырёхугольных пирамид, основаниямикоторых служат описанные выше квадраты, а боковые треугольные грани «вдавлены» в тело и касаютсясвоими вершинами средних точек противоположных углублений. Итоговая звёздчатая форма кубооктаэдра является соединением двух тетраэдров, Кеплеровой stellaoctangula, итоговой звёздчатой формы октаэдра и трёх правильных четырёхугольных призм, общимпересечением которых является исходный куб. Каждое основание этих призм представляет собой глубокуювпадину, образованную четырьмя рёбрами. 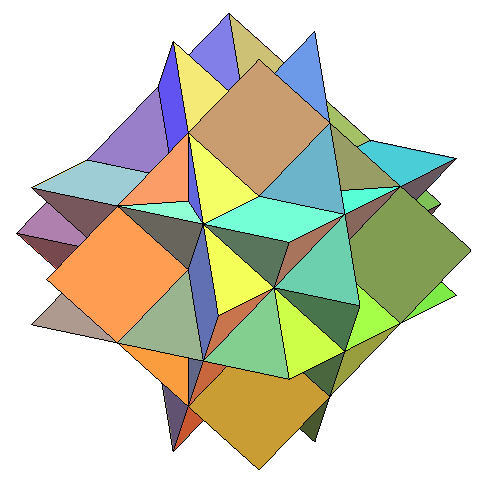 ЗВЕЗДЧАТЫЙ ИКОСОДОДЭКТАЭДР Звёздчатый икосододекаэдр — звёздчатый многогранник с 32 гранями, из которых 12 являютсяправильными пятиугольниками, а остальные 20 — правильнми треугольниками.Этот многогранник являет собой пример соединения двух платоновых тел — додекаэдра и икосаэдра; егоможно так же рассматривать как первую звёздчатую форму икосододекаэдра. С него начинается так называемая «основная линия» звёздчатых форм икосододекаэдра, к которой относятсямногогранники, полученные добавлением к исходному телу отсеков, полностью покрывающих его поверхность. Поэтому 12 невысоких пятиугольных пирамид и 20 маленьких треугольных пирамид закрывают внутреннийикосододекаэдр. Многогранник представляет собой соединение 10 тетраэдров, на котором «тень» большого додекаэдраоставила следы в виде отверстий на дне впадин; из-за этого нутро многогранника становится видимым идоступным. Завершающие звёздчатые формы любых многогранников всегда вызывают особый интерес. Перед намизавершающая форма икосододекаэдра. Не правда ли, чем-то она напоминает вспышку фейерверка, когда изодной точки в разных направлениях разлетаются огненные звёзды и путь их ясно виден на фоне ночного неба. Но никакой фейерверк не сможет передать удивительной упорядоченности и математической точности этогомногогранника, лучи которого чётко группируются в 12 заметных «короноидальных» групп. Вы без трудаобнаружите в нём завершающие звёздчатые формы додекаэдра и икосаэдра. Большой звёздчатый додекаэдрлишь слегка выступает из тела многогранника маленькими трёхгранными отсеками, похожими на кустикитравы у подножия гигантского дуба. А пятёрки вершинных пиков завершающего звёздчатого икосаэдраобразуют основу каждой «короны». Но промежутки между этими пиками заполнены другими — тонкими и длинными, а всё соединение из пиков и составляет целую «корону». 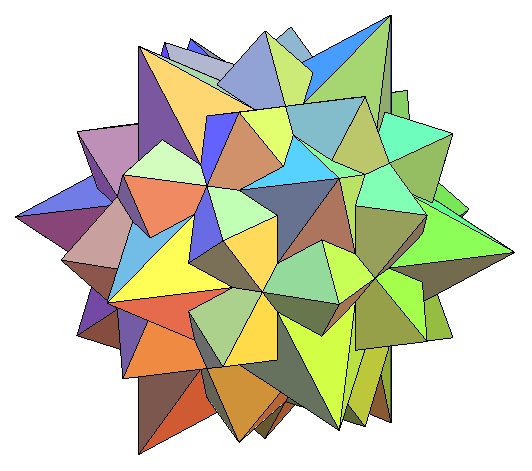 |
