Діагностика_Лаб2_v1.3(final). Звіт по лабораторній роботі 2 з дисципліни Діагностика та надійність гкс Виконали
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
    Міністерство освіти і науки України Національний технічний університет України „КПІ” Факультет інформатики та обчислювальної техніки Кафедра технічної кібернетики Звіт по лабораторній роботі №2 з дисципліни «Діагностика та надійність ГКС» Виконали: студенти ІV курсу гр. ІК- 12 Калініна І.В. Коваль Д.Ю. Сіпаков Г.О. Шевчук Д.Д. Перевірив: К.т.н., доцент Бурлаков В.М. Київ 2015 Короткі теоретичні відомості Резервування - метод підвищення надійності ТС за рахунок введення надмірності. Під надмірністю при цьому розуміють додаткові засоби і можливості понад мінімально необхідних для виконання ТС заданих функцій. Розрізняють три основних види резервування: - структурне, - інформаційне, - часове. Структурне резервування (або апаратне) передбачає використання надлишкових елементів ТС. Його суть полягає в тому, що в мінімально необхідний варіант системи, елементи якої називають основними, вводяться додаткові елементи, вузли, пристрої або навіть замість однієї системи передбачається використання декількох ідентичних систем. При цьому надлишкові резервні структурні елементи, вузли, пристрої і т.д. призначені для виконання робочих функцій при відмові відповідних основних елементів, вузлів і пристроїв. При активному резервуванні структура ТС така, що при появі відмови вона перебудовується й відбувається відновлення її працездатності, тобто відбувається як би «саморемонт» ТС, тобто ТС активно реагує на появу відмови. При пасивному резервуванні ТС відмова одного або навіть декількох елементів не впливає на її роботу. Елементи з'єднані постійно і перестроювання структури не відбувається. ТС як би пасивно чинить опір появі відмов елементів. За режимом роботи резерву для активного резервування розрізняють навантажений, полегшений і ненавантажений резерви. Навантажений резерв - резервний елемент знаходиться в тому ж режимі, що й основний. При цьому рахується, що характеристики надійності резервних елементів у період їх перебування в якості резервних і в період їх використання замість основних після відмови останніх залишаються незмінними. Полегшений резерв - резервний елемент знаходиться в менш навантаженому режимі, ніж основний. При цьому рахується, що характеристики надійності резервних елементів у період їх перебування в якості резервних вище, ніж у період їх використання замість основних після їх відмови. Ненавантажений резерв - резервний елемент практично не несе навантаження до початку виконання ним функцій основного елемента. При цьому рахується, що такий резервний елемент, перебуваючи в резерві, відмовляти не повинен, тобто володіє в цей період «ідеальною»надійністю. У період же використання резервного елемента замість основного після відмови останнього надійність резервного елемента стає рівною надійності основного. Методика розрахунку ймовірності безвідмовної роботи для послідовних та паралельних структур: 2 1
Виходячи з того, що ймовірність безвідмовної роботи для обох елементів і ймовірність їх відмови утворюють повну групу подій, ймовірність безвідмовної роботи паралельної структури обчислюємо як: 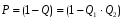 Завдання Для системи без відновлення елементів у процесі функціонування визначити ймовірність безвідмовної роботи P(t) за час t=10 г, та середній наробіток до відмови Т, коли відомі ймовірності безвідмовної роботи елементів за цей час: P1 = 0,5 P2 = 0,6 P3 = 0,7 P4 = 0,8 P5 = 0,85 P6 = 0,55 P7 = 0,9 P8 = 0,9 P9 = 0,96 P10 = 0,97. Припустити, що наробітки до відмови мають експоненціальний розподіл. На малюнках навантажений резерв позначено а ненавантажений резерв позначено Варіанти надійнисних схем мають вигляд : 2.8.  2.10.  Виконання Спочатку визначимо інтенсивності відмов елементів із співвідношення 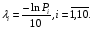 Маємо 1 = 6,910-2 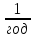 ; 2 = 5,110-2 ; 2 = 5,110-2 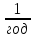 ; 3 = 3,610-2 ; 3 = 3,610-2 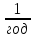 ; ;4 = 2,210-2 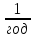 ; 5 = 1,610-2 ; 5 = 1,610-2 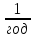 ; 6 = 6,010-2 ; 6 = 6,010-2 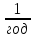 ; ;7 = 8 = 1,110-2 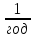 ; 9 = 4,110-3 ; 9 = 4,110-3 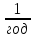 ; 10 = 3,0410-3 ; 10 = 3,0410-3 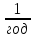 . .Згідно з припущенням ймовірності безвідмовної роботи елементів за довільний час t має вигляд : 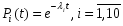 . .
 Рис. 1. Для подальшого обчислення показників надійності системи застосуємо метод послідовного структурного укрупнення.  Рис. 2 Визначимо ймовірність безвідмовної роботи за час t структури N. Це – ненавантажене резервування без відновлення, і тому розподіл наробітку до відмови структури дорівнює розподілу суми наробіток до відмови елементів. Отже, щільність розподілу наробітку до відмови є згорткою щільностей розподілів наробіток до відмови елементів: 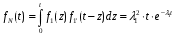 . .Ймовірність відмови за час t дорівнює 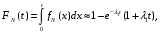 а ймовірність безвідмовної роботи 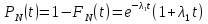 Обчислимо показники надійності структури D. Для цього застосуємо метод особливого елемента. Позначимо через 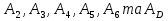 події, що означають безвідмовну роботу за час t відповідного елемента або структури. події, що означають безвідмовну роботу за час t відповідного елемента або структури.Як особливий візьмемо елемент 4. За формулою повної ймовірності маємо 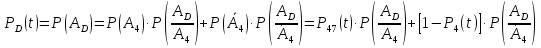 Обчислимо 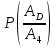 . Це є ймовірність безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 3. . Це є ймовірність безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 3.2 3 5 6 Рис.3 Вона дорівнює 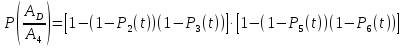 Аналогічно, 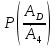 дорівнює ймовірності безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 4. дорівнює ймовірності безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 4.6 3 2 5 Рис. 4 Тобто 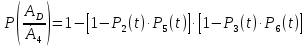  Після укрупнення структури D до одного елемента остаточно одержуємо послідовну структуру з двох елементів, що має вигляд зображений на рис. 5. N D Рис.5 Отже, ймовірність безвідмовної роботи всієї системи за час t дорівнює 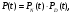 де PN(t) та PD(t) визначені вказаними вище співвідношеннями. Для обчислення P(t) за заданий час потрібно в ці співвідношення підставити t=10 год. Одержуємо 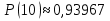 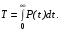 Середній наробіток до відмови обчислюється за формулою Середній наробіток до відмови обчислюється за формулоюЗастосовуючи систему Mathcad, одержуємо T 32,13 год.
 Рис. 6.  Рис. 7. Використовуючи ті самі методи, що й в попередній схемі, отримуємо: 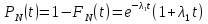 Показники надійності структури В: 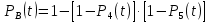 Особливим елементом обираємо структуру В. За формулою повної ймовірності маємо 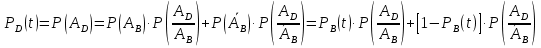 Обчислимо 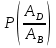 . Це є ймовірність безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 8. . Це є ймовірність безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 8.2 3 6 7 Рис.8 Вона дорівнює 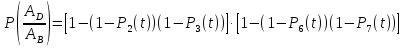 Аналогічно, 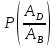 дорівнює ймовірності безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 9. дорівнює ймовірності безвідмовної роботи за час t послідовно-паралельної структури, що зображена на рис. 9.7 3 2 6 Рис. 9 Тобто 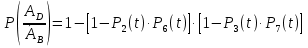  Після укрупнення структури D до одного елемента остаточно одержуємо послідовну структуру з двох елементів, що має вигляд зображений на рис. 10. 10 D N Рис.10 Отже, ймовірність безвідмовної роботи всієї системи за час t дорівнює 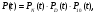 де PN(t) та PD(t) визначені вказаними вище співвідношеннями. Для обчислення P(t) за заданий час потрібно в ці співвідношення підставити t=10 год. Одержуємо 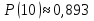 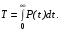 Середній наробіток до відмови обчислюється за формулою Середній наробіток до відмови обчислюється за формулоюЗастосовуючи систему Mathcad, одержуємо T 30,52 год. Висновок В даній роботі для двох заданих систем було обчислено ймовірність безвідмовної роботи P(t) за час t=10 г, та середній наробіток до відмови Т, коли відомі ймовірності безвідмовної роботи елементів за цей час. |

 Для послідовних структур :
Для послідовних структур :