1. 2 Построение временных и частотных характеристик объекта по каналу управления при наличии и отсутствии запаздывания
 Скачать 395.73 Kb. Скачать 395.73 Kb.
|
1.2 Построение временных и частотных характеристик объекта по каналу управления при наличии и отсутствии запаздывания.Построение переходной функции  Так как запаздывание только сдвигает переходную функцию на время , то вывод переходной функции будем делать для аналогичного звена без запаздывания, а «» - учтем в окончательной формуле. Таким образом, передаточная функция объекта имеет вид:  Входной сигнал  Изображение выходного сигнала имеет вид:  Определим характер переходного процесса по дискриминанту характеристического полинома   Так как дискриминант меньше нуля, значит корни комплексные и переходная функция объекта по каналу управления имеет колебательный характер. Определим корни характеристического полинома. Для этого воспользуемся функцией solve в среде Mathcad.  Так как вещественная часть корней отрицательная, колебания носят затухающий характер. При этом частота колебаний должна быть равна 0,07198 Для построения переходной функции воспользуемся обратным преобразованием Лапласав среде Mathcad  Теперь учтем влияние запаздывания и построим переходную функцию по каналу управления при наличии запаздывания и при его отсутствии.  Рисунок 1.1 – Переходная функция каналу управления. Однако одно и то же дифференциальное уравнение может иметь множество решений, зависящих от начальных условий и характера входного воздействия x(t), что неудобно при сопоставлении динамических свойств различных элементов. Поэтому было решено характеризовать эти свойства элемента только одним решением дифференциального уравнения, полученным при нулевых начальных условиях и одном из типовых воздействий: единичном ступенчатом, дельта-функции, гармоническом, линейном. Наиболее наглядное представление о динамических свойствах элемента дает его переходная функция h(t). Переходная функция h(t) элемента – изменение во времени выходной величины y(t) элемента при единичном ступенчатом воздействии и нулевых начальных условиях. Переходная функция может быть задана: · в виде графика; · в аналитическом виде. Переходная функция, как и любое решение неоднородного (с правой частью) дифференциального уравнения (2.19), имеет две составляющие: · вынужденную hв(t) (равна установившемуся значению выходной величины); · свободную hс(t) (решение однородного уравнения). Вынужденную составляющую можно получить решая уравнение (2.19) при нулевых производных и x(t) = 1 Свободную составляющую получаем решая уравнение (2.19) при нулевой правой части hс(t) = где pk – k-й корень характеристического уравнения (в общем случае комплексное число); Сk - k-я постоянная интегрирования (зависит от начальных условий). Характеристическое уравнение – алгебраическое уравнение, степень и коэффициенты которого совпадают с порядком и коэффициентами левой части линейного дифференциального уравнения вида (2.19) a0 pn + a1 pn –1 +…+ an = 0. (2.22) Построение амплитудно-частотной характеристики Передаточная функция канала:  Так как запаздывание не влияет на амплитудно-частотную характеристику, то его можно исключить из передаточной функции:  Сделаем замену   Находим выражение для АЧХ объекта по каналу управления   Построим АЧХ  Рисунок 1.2 – Амплитудно-частотная характеристика объекта по каналу управления 1. ЧХ 2. ЧХ Доказательство периодичности функций следует из того, что их аргумент В зависимости от используемой шкалы частот период ЧХ, АЧХ и ФЧХ равен Если коэффициенты ПФ вещественные (а другие не рассматриваются), то АЧХ будет четной, а ФЧХ –нечетнойфункцией частоты [1]: Напомним, что четнойназывается такая функция, которая не изменяет своего значения при изменении знака переменной. Если же при изменении знака переменной изменяется знак функции, а ее абсолютное значение сохраняется неизменным, то такая функция называется нечетной. На практике представляют интерес графики АЧХ и ФЧХ в основнойполосе частот Получим частотную характеристику 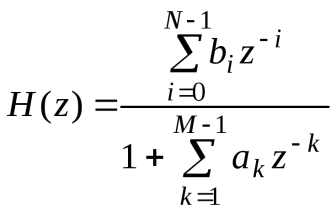 . .Выполнив замену запишем частотную характеристику в виде  . (1.74) . (1.74)Раскроем экспоненты по формуле Эйлера, например, в знаменателе после чего выделим вещественные и мнимые части в числителе и знаменателе (1.74): где индексы «ч» и «з» означают числитель и знаменатель. Определим модуль (АЧХ) и аргумент (ФЧХ) частотной характеристики  ; (1.77) ; (1.77)Полученные выражения используются для расчета АЧХ и ФЧХ в основной полосе частот. Построение фазо-частотной характеристики ФЧХ при отсутствии запаздывания:  При 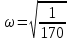 выражение выражение  и и 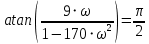 . .Следовательно, при   А при   Внесение запаздывание добавляет линейно убывающие фазовые сдвиги и выражение для ФЧХ изменится следующим образом: При   А при   Построим графики ФЧХ объекта по каналу управления с запаздыванием и без.  Рисунок 1.3 – ФЧХ объекта по каналу управления. Построение ФЧХ коэффициента передачи: Для построения ФЧХ непосредственно на основе схемы необходимо сохранить характер реактивного сопротивления. Поэтому эквивалентные схемы изобразим не для = 0, а для 0, не для a для
В соответствии с определением коэффициента передачи по напряжению Следовательно, Для удобства положим Построим векторные диаграммы для схемы рисунка 2.7а и б, соответственно:
Исходя из рис.2.8а, разность фаз между входным и выходным напряжениями составило 00, т.е.
Построение амплитудно фазовой характеристики При наличии запаздывания      Без запаздывания  Построим графики АФХ  Рисунок 1.4 – АФХ объекта по каналу управления 1.3 Построение временных и частотных характеристик объекта по каналу возмущения 1Построение переходной функции Передаточная функция  Так как запаздывание только сдвигает переходную функцию на время , то вывод переходной функции будем делать для аналогичного звена без запаздывания, а «» - учтем в окончательной формуле. Таким образом, передаточная функция объекта по этому каналу имеет вид: 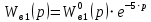 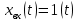 –входной сигнал. –входной сигнал.Изображение выходного сигнала имеет вид:  Знаменатель этой дроби уже представлен в виде простейших множителей, поэтому сразу находим значение коэффициентов разложения ее на сумму дробей.   Приводим левую часть к общему знаменателю:  Следовательно:  при свободном члене:   при  : :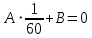  при  : : 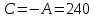 Получаем:  Находим оригинал: 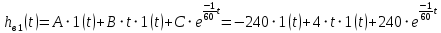 Учтем явление запаздывания:  Таким образом, при  . А при . А при 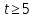 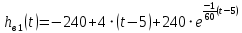 Построим переходную функцию:  Рисунок 1.5 – Кривая разгона объекта по каналу возмущения 1 Пусть теперь f(t) непериодическая функция и пусть при Найдем предельное выражение ряда Фурье f(t). Так как функция f(t) известна, то коефициенты ряда можно найти по ф.(43). Если выполнять интегрирование (43) при известной функции f(t), то получим Учитывая ф.(47) можно записать в виде: Обозначив Формула (49) представляет интеграл Фурье, где F(jω) - коефициетная функция, так как выполняет ролькоефициентов обычного родаФурье и может быть выражена через f(t). Действительна при 64. Формула (49) представляет интеграл Фурье, где F(jω) - коефициетная функция, так как выполняет ролькоефициентов обычного родаФурье и может быть выражена через f(t). Действительна при Подставив значение или (51) Формула (51) называется интегралом Лапласа. Интеграл Фурье и интеграл Лапласа являются двумя взаемно обратными преобразователями, тоесть первое является решением второго и наоборот. Интеграл Фурье и Лапласа можно обьеденить в одно уравнение Для практическаго решения задач пользуемся более удобным Это уравнение называют двойным интегралом Фурье. Представление f(t) двойным интегралом Фурье получим при условии Если это уравнение не выполняемо, то чтобы применить (52), необходимо предварительно умножить f(t) на функцию Так как его условия выполняются представим его двойным интегралом Построение амплитудно-частотной характеристики Передаточная функция канала:  Исходя из понятия амплитуды комплексного числа, определим АЧХ как: 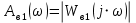 Используя среду Mathcad,рассчитаем и построим график АЧХ объекта по каналу возмущения 1. 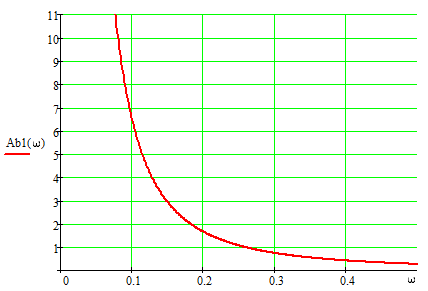 Рисунок 1.6 – АЧХ объекта по каналу возмущения 1 В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций: Часто в теории цепей используют нормированную или рабочую передаточную функцию четырехполюсника:  , (1.3) , (1.3)которая получается путем нормирования (1.1) множителем  . . Как всякую комплексную величину Н можно представить в показательной форме: где Рассмотрим комплексную передаточную функцию по напряжению  , (1.5) , (1.5)Подставляя в (1.5) запись комплексных действующих значений получим  . .Из сравнения этого выражения с (1.4) видно, что  , ,т. е. модуль комплексной передаточной функции по напряжению (или комплексного коэффициента усиления по напряжению) показывает во сколько раз изменяется действующее значение (амплитуда) гармонического колебания напряжения на выходе цепи по сравнению с аналогичным значением на входе цепи, а аргумент этой функции определяет сдвиг фаз между гармоническими колебаниями напряжения на входе и выходе. Точно так же можно найти:  . .Все сказанное выше о коэффициенте передачи по напряжению справедливо и для коэффициента передачи по току.  Если мы будем изменять частоту гармонического колебания, то выражение (1.4) следует записать в виде: Функция частоты Функция частоты Комплексную передаточную функцию где Re и Im означают реальную и мнимую части комплексной величины. Из теории комплексных величин известно, что  Построение фазо-частотной характеристики сходя из понятия фазы комплексного числа, определим ФЧХ как:  Используя среду Mathcad,рассчитаем и построим график ФЧХ объекта по каналу возмущения 1.При этом необходимо помнить, что функция  возвращает значения из области возвращает значения из области 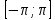 , а значит, в точках разрыва функции необходимо добавлять сдвиг на , а значит, в точках разрыва функции необходимо добавлять сдвиг на  . На области исследуемых частот получаем следующую функцию: . На области исследуемых частот получаем следующую функцию: Построим график ФЧХ  Рисунок 1.7 – ФЧХ объекта по каналу возмущения 1. Построение амплитудно фазовой характеристики Амплитудно-фазовая характеристика объекта по каналу возмущение 1 определяется следующим выражением: 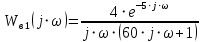 Рассчитаем и построим график АФХ в среде Mathcad  Рисунок 1.8 – АФХ объекта по каналу возмущения 1 1.4 Построение временных и частотных характеристик объекта по каналу возмущения 21) Для составления передаточной функции по управлению Wy(p) необходимо положить возмущающее воздействие m1(p) =0. Wy(p) =X1(p) /u(p) Система примет вид:  После математических преобразований и подстановки Cm=10; fm=10; u=220; a21=0. 025; a31=22; a32=10, получим: 2) Для составления передаточной функции по возмущению WВ(p) необходимо u(p) =0. WВ(p) =X1(p) /m1(p) Система примет вид  После математических преобразований и подстановки Cm=10; fm=10; u=220; a21=0. 025; a31=22; a32=10, получим: Составим структурную схему: 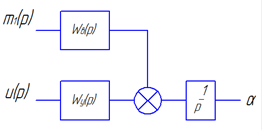 Рисунок 3. 1-структурная схема. На схеме и . Воспользуемся пакетом Simulink системы MatLab.  Рисунок 3. 2 - схема моделирования Далее представлены показания Scope, Scope1: Scope Scope1   Рисунок 3. 3 - показания Scope, Scope1 Построение временных и частотных характеристик объекта управления Используя полученные ранее передаточные функции по управлению = и возмущению получим ЛАЧХ L(w) =20lg|W(j w) | [dB] и ЛФЧХ j(w) =arctg(“v (w) /u (w)). 1) Построим ЛАЧХ и ЛФЧХ для функции по управлению: Ly(w) =20lg(0. 01) - 10lg(-0. 001936w2+(1-0. 01w2) 2) - 20lg(w) jУ(w) =-р - arctg((0. 001w2-1) /0. 001936w) Непосредственно в MATLAB набираем: a = [0. 01]; b = [0. 0002 0. 044 1 0] [h, w] = freqs(a, b); mag = abs(h); phase = angle(h); subplot(2,1,1), semilogx(w, 20*log10(mag)); grid on; ylabel('dB'); subplot(2,1,2), semilogx(w,phase*180/pi); grid on; ylabel('rad'); 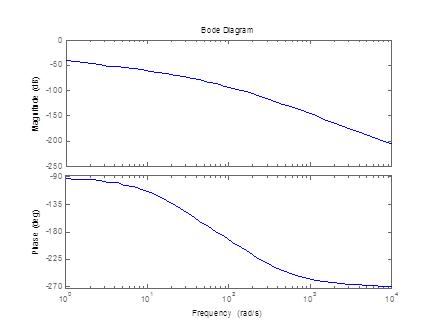 Рисунок 4.1 - ЛАЧХ и ЛФЧХ для функции по управлению 2) Построим ЛАЧХ и ЛФЧХ для функции по возмущению: 1) LВ(w) =10lg(0. 000484+10-8w) - 20lg(w) - 10lg((1-2*10-4w) 2-0. 001936w2) jВ(w) =-(arctg0. 0045w - arctg((0. 0002w-1) /0. 001936w) Непосредственно в MATLAB набираем: a = [0. 0001 0. 0022]; b = [0. 0002 0. 044 1] [h, w] = freqs(a, b); mag = abs(h); phase = angle(h); subplot(2,1,1), semilogx(w, 20*log10(mag)); grid on; ylabel('dB'); subplot(2,1,2), semilogx(w,phase*180/pi); grid on; ylabel('rad');  Рисунок 4.2 - ЛАЧХ и ЛФЧХ для функции по возмущению | ||||||||

 0
0 
